The 2020 ICPC Asia Macau Regional Contest A - Accelerator
题目链接:https://codeforces.com/gym/103119/problem/A
推荐博客:https://fanfansann.blog.csdn.net/article/details/118528285
题意:(复制上面推荐博客的)

思路:
上述式子化简,可以得到a1*a2*...*an + a2*a3*...*an + ... + an
求该式子所有排列的期望,就相当于:所有排列的贡献之和 / 排列数
全排列个数显然是 n!
关键在于怎么计算所有排列之和,先画画图,假设数组是【1,2,3】
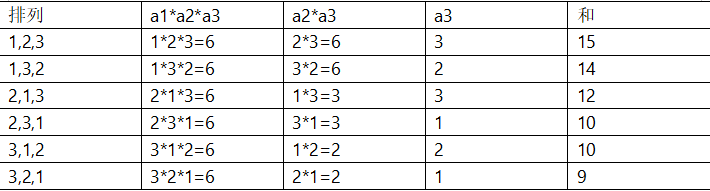
那么答案就是(15+14+12+10+10+9) / 6 = 70 / 6
按列来考虑,假设 f(x)是 “ 长度为x的所有排列的贡献和 ” ,则f(3) = 6*6 = 36,f(2) = (6+3+2) * 2 = 22, f(1) = (3+2+1)*2 = 12, 总和就是f(1)+f(2)+f(3) = 70
问题就转化成如何快速求 f(x)
假设求f(2),那么所有排列就是{【1,2】,【1,3】,【2,3】,【2,1】,【3,1】,【3,2】}
可见,就是在3个数中任选2个出来,就可以组成一个序列,而且每个序列的数字可以交换位置。
这像什么呢?在一堆数中随意挑几个数出来合在一起求贡献,应该要想到多项式相乘
对于单个ai,我们先构造出他的多项式,
关于幂次,ai只有取和不取,所以幂次设成0和1,幂次为0代表不取这个数,幂次为1代表取这个数,
关于系数,当不取ai的时候,无贡献,相当于乘1,当取ai的时候,贡献为ai,所以幂次为0的系数为1,幂次为1的系数为ai
单个ai的多项式如图

我们把所有ai的多项式乘起来,那么结果多项式中,幂次为x的系数就是长度为x的排列的贡献和(注意:这里的【1,2】和【2,1】是一种排列)
举个例子,假设只有a1和a2
多项式相乘:(1 * X0 + a1 * x1) * (1 * X0 + a2 * x1) = = 1 * X0 + (a1+ a2)* x1 + a1 * a2 * X2
幂次为2的系数是 a1 * a2, 并没有出现 a2 * a1
这和我们的f(x)还有点差距,少了一些排列的贡献和,但是注意到没有算进去的排列,都可以通过改变顺序转换成某个算出来的排列,比如a2 * a1 可以改变顺序变成 a1 * a2
可以通过算期望来计算出f(x),假设g(x)为幂次为x的系数,期望 = 权重* 概率 ,权重为g(x),概率为 n! / C(n,x) ,化简一下概率就是 x! * (n-x)!
说明一下这个概率是怎么算的,n!表示一共会出现的排列数(可以看上面的表格,不管x是多少,排列数都是一样的),C(n,x) 表示n个数里面选x个组成的排列数,即g(x)是由多少项相加得到
g(x)乘这个概率就相当于把没算的部分加上去,得到f(x)
至此,我们可以算出所有的f(x),那么答案就是(f(1) + f(2) + ... + f(n)) / n!
算g(x)可以用NTT,n个多项式相乘,可以看成线段树的操作,每个节点看成一个多项式,线段树每个最底层的节点相当于一个多项式,往上合并,两个节点合并的时候使用NTT合并,一直合到根节点就可以算出n个多项式相乘的结果
看了很多博客,这种操作应该叫分治NTT,不过我喜欢看成线段树来理解。总的时间复杂度是O(n * logn * logn)
注意:编译器选这个有优化的,不然大概率TLE
代码:
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e6 + 7;
const ll inf = 0x3f3f3f3f3f3f3f3f;
ll n;
const ll p=998244353,G=3,Gi=332748118,mod = 998244353;
ll limit=1,L=0,r[maxn];
ll a[maxn],jie[maxn],q[maxn],f1[maxn],f2[maxn];
ll qpow(ll a,ll n) {
ll c=1;
while(n) {
if(n&1) c = c * a % mod;
n >>= 1;
a = a * a % mod;
}
return c;
}
ll C(ll n,ll m) {
return jie[n] * q[m] % p * q[n-m] % p;
}
void init(ll len) {
L = 0;
limit = 1;
while(limit<=len) limit<<=1,L++;
for (int i=0; i<limit; ++i)
r[i] = (r[i>>1]>>1) | ((i&1)<<(L-1));
}
void NTT(ll *A,int type) {
for (int i=0; i<limit; ++i)
if(i<r[i]) swap(A[i],A[r[i]]);
for (int mid=1; mid<limit; mid<<=1) {
ll Wn = qpow(type==1?G:Gi,(p-1)/(mid<<1));
for (int j=0; j<limit; j+=(mid<<1)) {
ll w=1;
for (int k=0; k<mid; k++,w=(w*Wn)%p) {
ll x=A[j+k],y=w*A[j+k+mid]%p;
A[j+k] = (x+y)%p;
A[j+k+mid]=(x-y+p)%p;
}
}
}
}
void gao(int l,int r,vector<ll> &f) {
if(l == r) {
f[0] = 1;
f[1] = a[l];
return;
}
int mid = l + r >> 1;
int len1 = mid - l + 1, len2 = r - mid;
vector<ll>w1(len1+7,0),w2(len2+7,0);
gao(l,mid,w1);
gao(mid+1,r,w2);
for (int i=0; i<=len1; ++i) f1[i] = w1[i];
for (int i=0; i<=len2; ++i) f2[i] = w2[i];
int len = len1 + len2;
init(len);
for (int i=len1+1; i<limit; ++i) f1[i] = 0;
for (int i=len2+1; i<limit; ++i) f2[i] = 0;
NTT(f1,1);
NTT(f2,1);
for (int i=0; i<=limit; ++i) f1[i] = (f1[i] * f2[i]) % p;
NTT(f1,-1);
ll inv = qpow(limit,p-2);
for (int i=0; i<=len; ++i) f[i] = f1[i] * inv % p;
}
void solve() {
scanf("%lld",&n);
for (int i=1; i<=n; ++i) scanf("%lld",&a[i]);
vector<ll>b(n+7,0);
gao(1,n,b);
ll ans = 0;
for (int i=1; i<=n; ++i) {
ans = (ans + b[i] * jie[i] % p * jie[n-i] % p + p) % p;
// printf("%d %lld %lld\n",i,jie[n] % p * qpow(C(n,i),p-2) % p,b[i]);
}
// printf("%lld\n",ans);
printf("%lld\n",ans * q[n] % p);
}
int main() {
jie[0] = 1;
for (int i=1; i<=100000; ++i) jie[i] = jie[i-1] * i % p;
q[100000] = qpow(jie[100000],p-2);
for (int i=100000-1; i>=0; --i) q[i] = q[i+1] * (i+1) % p;
int t;
scanf("%d",&t);
while(t--) {
solve();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号