LeNet（Jax/Flax）实现

LeNet

LeNet，它是最早发布的卷积神经网络之一，因其在计算机视觉任务中的高效性能而受到广泛关注。 这个模型是由AT&T贝尔实验室的研究员Yann LeCun在1989年提出的（并以其命名），目的是识别图像 (LeCun et al., 1998)中的手写数字。 当时，Yann LeCun发表了第一篇通过反向传播成功训练卷积神经网络的研究，这项工作代表了十多年来神经网络研究开发的成果。
当时，LeNet取得了与支持向量机（support vector machines）性能相媲美的成果，成为监督学习的主流方法。 LeNet被广泛用于自动取款机（ATM）机中，帮助识别处理支票的数字。 时至今日，一些自动取款机仍在运行Yann LeCun和他的同事Leon Bottou在上世纪90年代写的代码。

模型结构

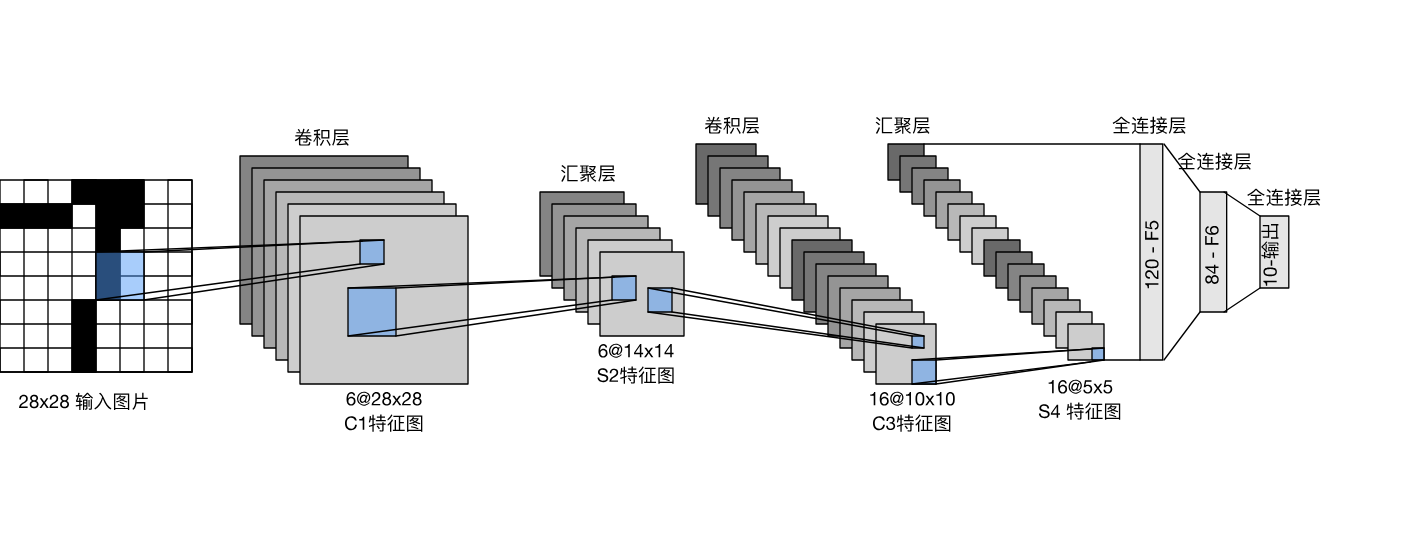
总体来看，LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成;
• 全连接层密集块：由三个全连接层组成。

Flax实现

import jax
import jax.numpy as jnp
from flax import nnx
from functools import partial


class LeNet(nnx.Module):
    def __init__(self, *, rngs: nnx.Rngs):
        self.features = nnx.Sequential(
            nnx.Conv(
                in_features=1,
                out_features=6,
                kernel_size=(5, 5),
                padding=(2, 2),
                rngs=rngs,
            ),
            nnx.sigmoid,
            partial(nnx.avg_pool, window_shape=(2, 2), strides=(2, 2)),
            nnx.Conv(
                in_features=6,
                out_features=16,
                kernel_size=(5, 5),
                padding="VALID",
                rngs=rngs,
            ),
            nnx.sigmoid,
            partial(nnx.avg_pool, window_shape=(2, 2), strides=(2, 2)),
        )
        self.fc = nnx.Sequential(
            lambda x: x.reshape(x.shape[0], -1),
            nnx.Linear(in_features=16 * 5 * 5, out_features=120, rngs=rngs),
            nnx.sigmoid,
            nnx.Linear(in_features=120, out_features=84, rngs=rngs),
            nnx.sigmoid,
            nnx.Linear(in_features=84, out_features=10, rngs=rngs),
        )

    def __call__(self, x):
        x = self.features(x)
        return self.fc(x)

模型测试

rngs = nnx.Rngs(42)
net = LeNet(rngs=rngs)
X = jax.random.normal(rngs.params(), shape=(1, 28, 28, 1), dtype=jnp.float32)

# Features
for i, layer in enumerate(net.features.layers):
    X = layer(X)
    print(f"features[{i}] ({layer.__class__.__name__}): 输出形状 {X.shape}")
# Fc
for i, layer in enumerate(net.fc.layers):
    X = layer(X)
    print(f"fc[{i}] ({layer.__class__.__name__}): 输出形状 {X.shape}")

输出

features[0] (Conv): 输出形状 (1, 28, 28, 6)
features[1] (PjitFunction): 输出形状 (1, 28, 28, 6)
features[2] (partial): 输出形状 (1, 14, 14, 6)
features[3] (Conv): 输出形状 (1, 10, 10, 16)
features[4] (PjitFunction): 输出形状 (1, 10, 10, 16)
features[5] (partial): 输出形状 (1, 5, 5, 16)
fc[0] (function): 输出形状 (1, 400)
fc[1] (Linear): 输出形状 (1, 120)
fc[2] (PjitFunction): 输出形状 (1, 120)
fc[3] (Linear): 输出形状 (1, 84)
fc[4] (PjitFunction): 输出形状 (1, 84)
fc[5] (Linear): 输出形状 (1, 10)