计算给定多项式在给定点x 处的值

计算给定多项式在给定点\(x\)处的值

方法1

\[f(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}+a_nx^n \]

double f_1(int n, double a[], double x) {
    int i;
    double p = a[0];
    for (i = 1; i <= n; i++)
        p += (a[i] * pow(x, i));
    return p;

}

方法2

多项式可以拆成如下形式：

\[f(x)=a_0+x(a_1+x(\cdots(a_{n-1}+x(a_n))\cdots) \]

double f_2(int n, double a[], double x) {
    int i;
    double p = a[n];
    for (i = n; i > 0; i--)
        p = a[n - 1] + x * p;
    return p;
}

计算给定多项式\(f(x)=\sum_{i=0}^9i\cdot x^i\)在给定点\(x=1.1\)处的值\(f(1.1)\)

#include <stdio.h>
#include <time.h>
#include <math.h>

#define MAXK 1e7
#define MAXN 10
clock_t start, stop;
double duration;

double f_1(int n, double a[], double x) {
    int i;
    double p = a[0];
    for (i = 1; i <= n; i++)
        p += (a[i] * pow(x, i));
    return p;

}

double f_2(int n, double a[], double x) {
    int i;
    double p = a[n];
    for (i = n; i > 0; i--)
        p = a[n - 1] + x * p;
    return p;
}


void compute_time(double function(), int n, double a[], double x) {
    start = clock();
    for (int i = 0; i < MAXK; i++)
        function(n, a, x);
    stop = clock();
    duration = ((double) (stop - start)) / CLK_TCK / MAXK;
    printf("Duration: %.2e s\n", duration);
}

int main(void) {
    double a[MAXN];
    compute_time(f_1, MAXN - 1, a, 1.1);
    compute_time(f_2, MAXN - 1, a, 1.1);
    return 0;
}

运行结果：

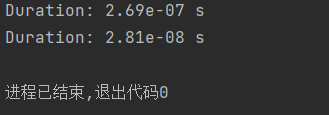
第二种方法比第一种方法快一个数量级