卷积神经网络入门（深度学习准备二）

1、卷积神经网络组成

卷积神经网络由 卷积层、池化层、全连接层组成，本文主要展示每一个层次的组成以及基本参数运算法则。

• 卷积层（Convolution Layer）

　　　卷积层的主要作用是对输入的数据进行特征提取，而完成该功能的是卷积层中的卷积核（Filter），卷积核可以看成是一个指定窗口大小的扫描器。扫描器通过一次又一次地扫描输入的数据，来提取数据中的特征。举个例子，假设有一个 32*32*3 地图像，其中 32*32 指图像的高度和宽度， 3 指图像的深度，即图像有三个色彩通道（R： red、G： green、B： blue）。我们定义一个3*3*3的卷积核，那么 3*3 就是指卷积核的高度和宽度， 3 指卷积核的深度，通常卷积核的高度和深度为 3*3 或者 5*5，深度同要是别的图像。如果输入的图像是单色彩通道的，那么卷积核的深度就是 1，以此类推。

　　　卷积核处理图像矩阵的方法如下：

 

 

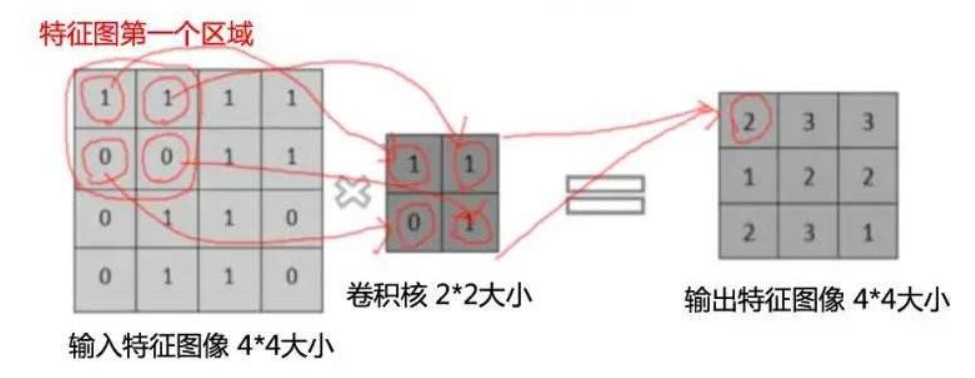
 　　　　如上图所示，输入图像是一个 4*4*1 的单色彩通道图像，卷积核大小为 2*2*1 ，步长为1（即每移动一次，卷积核滑动的窗口位置变化），每一次卷积的操作过程就是将对应位置相乘，求和得到输出特征图矩阵的位置。

　　　　对于第一个元素，假设输入图像矩阵为W，卷积核矩阵为X，输出图像矩阵为Z，那么：

　　　　Z00=W00*X00+W01*X01+W10*X10+W11*X11;

　　　　Z01=W01*X00+W02*X01+W11*X10+W12*X11;

　　　　……

　　　　Z22=W22*X00+W23*X01+W32*X10+W33*X11;

　　　　

　　　　卷积效果可以通过边界像素填充方式提升。我们在对输入图像进行卷积之前，有两种边界像素填充方式可以选择，分别是Valid和Same。Valid就是直接对输入图像进行卷积，不对输入图像进行任何前期处理和像素填充，这种方式可能会导致图像中部分像素点不能被滑动窗口（卷积核）捕捉；Same方式则是在输入图像之前将输入图像的最外层加上指定层数的值全为0的像素边界，这样能够使得输入图像的全部像素都能别滑动窗口（卷积核）捕捉。具体可参照下图。

　　　　Valid模式，输入图像5*5*1，卷积核3*3*1，卷积核步长为1：

 

　　　　Same模式，输入图像7*7*1，卷积核3*3*1，卷积核步长为2：

 

 

 

 

 （上图转载自https://blog.51cto.com/gloomyfish/2108390，作者gloomyfish ）

 

通过对卷积过程的计算，我们可以得出一个卷积的通用公式：

 

 

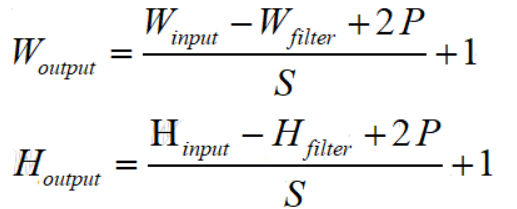
　　其中W（Weight）和H（Height）分别表示图像的宽度和高度，下标 input 表示输入图像的相关参数，output 表示输出图像的相关参数，filter 表示卷积核相关的参数，S表示卷积核的步长，P（Padding）表示在图像边缘增加的边界层数。如果选择的是 Same 模式，那么 P 的值等于图像增加的边界层数；而 Valid 模式下，P = 0.

　　用一个实例来说明：对于一个 7*7*1 的输入图像，图像最外层使用了一层边界像素填充，卷积核大小为 3*3*1，步长为1，使用的是Same模式，那么输出图像的宽度和高度为为（7-3+2*1)/1 + 1 =7，深度同输入图像，即输出图像深度为 1，单色彩通道。

　　其中还可以加入偏置，即如同前一篇博文所讲（https://www.cnblogs.com/Rebel3/p/11821541.html），类似于这里只计算了 z=W^T*X，之后可以再加入b作为偏置使得图像不经过原点。

• 池化层

　　池化层可以看成是卷积神经网络中的一种提取输入数据的核心特征的方式，不仅实现了对数据的压缩，还减少了参与模型运算的参数，从而提高了计算效率。池化层处理的输入数据一般情况下是经过卷积操作之后生成的特征图。常用的池化层方法是最大池化层和平均池化层，如下图所示：

 

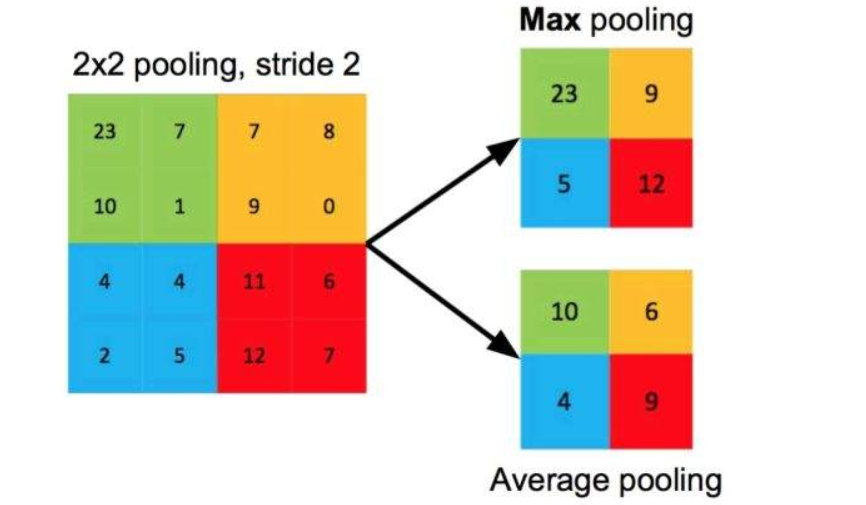
　　　　池化层也需要定义一个类似于卷积核的滑动窗口，称之为目标特征图，而输入的卷积层的原始输入数据称为原特征图。目标特征图的宽度和高度、步长类似卷积核，在此不再赘述，最大池化层就是将一个滑动窗口的最大值赋值给目标特征图相应位置。而平均池化层就是将一个滑动窗口内的数值求平均值，将平均值赋值给目标特征图对应位置。（平均分母为滑动窗口内数的个数）

　　　　同样的，我们也可以总结出一个适用于池化层的通用公式：

　　　　其中W（Weight）和H（Height）分别表示图像的宽度和高度，下标 input 表示输入图像的相关参数，output 表示输出图像的相关参数，filter 表示卷积核相关的参数，S表示滑动窗口的步长。

　　　　同样的，举个例子，由卷积层得到某图像的特征图为 16*16*6 大小，池化层的滑动窗口大小为 2*2*6，步长 stride 为 2，于是可以得到目标特征图大小为[(16-2)/2+1]*[(16-2)/2+1]*6=8*8*6,得到的特征图宽度和高度比原特征图压缩了近一半，这也印证了池化层的作用——最大限度地提取输入的特征图的核心特征，还能对输入的特征图进行压缩。

• 全连接层

　　全连接层主要作用是将输入图像在经过卷积和池化操作后提取的特征进行压缩（不难看出，卷积层提取特征图，池化层压缩特征图并提取核心特征，全连接层压缩特征），并根据压缩的特征完成模型的分类功能。

　　举个例子：假设对于一张图片，我们经过卷积和池化过程之后，得到了特征矩阵，大小为1*3072，而全连接层的权重参数矩阵为3072*10，即如下图所示

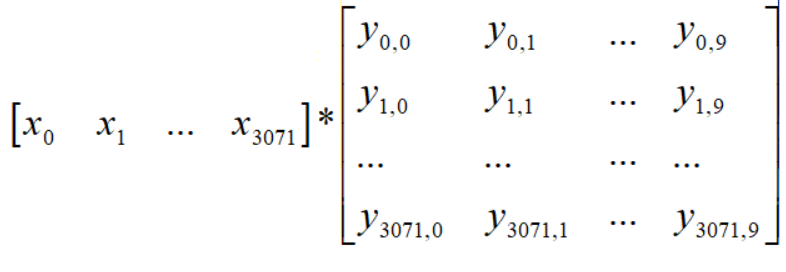
　　则在全连接之后，得到的将是一个1*10的核心特征矩阵，这10个参数已经是一个分类的结果，再经激活函数的进一步处理，就能让我们的分类预测结果更加明显。

 

2.GoogleNet的改进

　　GoogleNet改进了Naive Inception的单元结构，Naive将输入分解成用 1*1 卷积核卷积，3*3 卷积核卷积，5*5 卷积核卷积，3*3 最大池化，然后各层结果通过channel串联，合并输出。Naive Inception有两个致命的缺点：

　　1：所有卷积层直接和前一层数据相连，导致计算量很大

　　2：最大池化层保留了原特征图的深度，导致输出的特征图深度只会3不断地加大

　　而GoogleNet的解决方案是使用1*1卷积核来聚合/发散特征图通道

　　现在来看一下1*1卷积核工作原理，假设原特征图是 50*50*100 大小，Padding=0，用1*1*100卷积核卷积，stride=1，那么卷积一次后得到输出特征图大小为50*50*1（怎么理解呢，不妨将50*50*100的特征图看成是一个长方体，然后用1*1*100在里面填充，因为深度（100）是一致的，所以深度方向只需要1个，而宽度和高度需要50*50个堆叠，所以最后输出特征图大小为50*50*1），如果原特征图卷积n次，那么每一次得到的都是50*50*1的子特征图，在深度上channel串联，所以最后得到的特征图应该是50*50*n大小。

　　不难看出，1*1卷积核使得原特征图能够在深度（也就是channel通道上）进行聚合和发散（注意，不改变特征图大小）。现在举一个更加复杂的例子：

　　假设有一个32*32*10的特征图，需要使他的深度为20，那么用3*3*10卷积核卷积，Padding=1，stride=1，需要多少次？原特征图大小为32*32*10，用之前的公式可以知道，目标特征图大小为32*32*1，然后再卷积20次（也就是一直所说的channel通道串联），那么需要用到的卷积参数就是 3*3*10*20=1800个卷积参数（20个卷积核不能说明问题，毕竟卷积核大小都不一样）。

　　那么假如先用1*1*10卷积核卷积呢？我们不妨先用1*1*10卷积核卷积原特征图32*32*10，Padding=0，stride=1，卷积五次得到目标特征图32*32*5，Padding=1，stride=1，然后再用3*3*5卷积核卷积20次，得到最后32*32*20目标特征图，生成的特征图和原来一样，但是卷积参数只需要1*1*10*5+3*3*5*20=950个，极大提升了模型的性能

　　下图为Naive Inception和GoogleNet中的Inception层对比图：

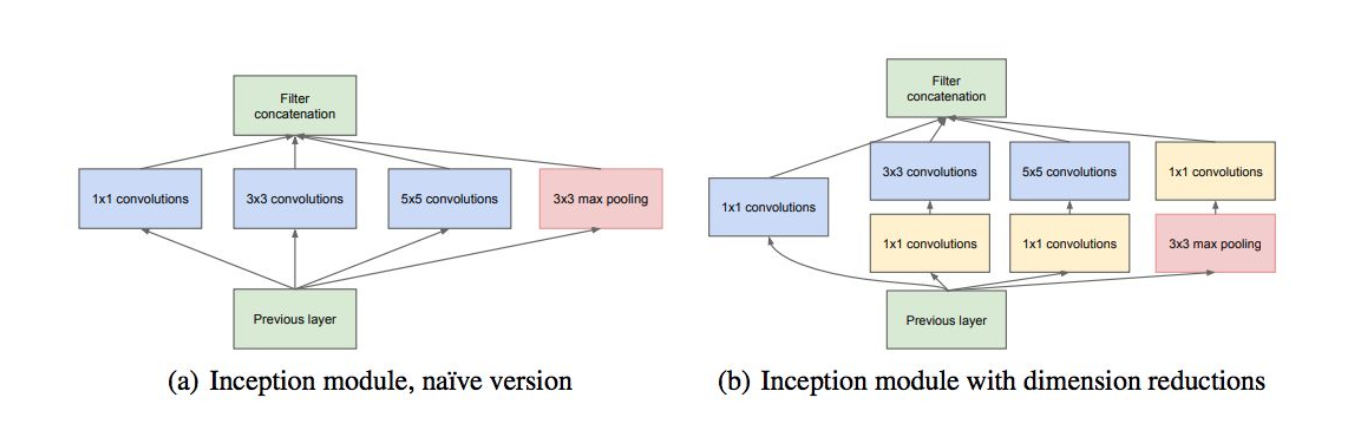
　　可以看见的是，在最大池化层之前也加上了1*1卷积核卷积中转，因而也避免了深度不断加大的情况。

3.ResNet（Residual NetWork残差网络）

　　由于深层次的卷积过程由于激活函数的原因会出现梯度消失的情况，而极易过拟合也导致模型质量下降。因而引入了残差机制，不仅避免了模型退化，反而提升了模型的性能。

 

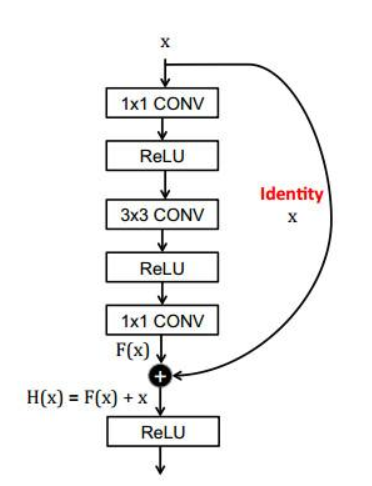
　　如上图所示，x经过了三次卷积，两次激活，在没有引入残差的网络里，输出只是将每次的激活机械式的堆叠，而残差网络中，则是添加了一个恒等模型，即输出不等于F(x)，而是x+F(x)的一个恒等变换，虽然多计算了一步，但是并不会给整个ResNet模型增加额外的参数和计算量，反而能够加快训练速度，提升模型的训练效果。

 

　　日积硅步以致千里！