算法学习笔记：DS-扫描线

DS：扫描线

前言

对于区间或区间子区间问题，我们有一些惯用套路简化问题。

很多区间问题都可以转化为平面上矩形问题，用扫描线就可以解决。具体地，我们把区间 \([l,r]\) 抽象为平面内的点 \((l,r)\)。

同时我们可以使用反演的思路，考虑每个值对哪些询问如何造成贡献，而不是对每次询问求贡献，这样在很多时候可以有效地平衡修改和查询实现的难度。

例题

UOJ637A 数据结构

给定长为 \(n\) 的序列，需要完成 \(m\) 次查询，将区间 \([l,r]\) 的数都加 \(1\) ，则整个序列有多少种不同的数。询问间独立。

sol：

我们先把区间的左右端点抽象为平面直角坐标系的 \(x\) 轴和 \(y\) 轴，这样每次询问就变成了一个点。

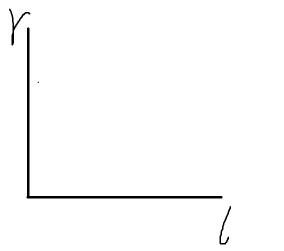
首先反演，考虑求每个数在哪些询问下可以产生贡献。

再充斥一下，转化为求一个数在哪些询问下没有出现过，因为出现过 \(1\)次，\(2\)次，\(3\)次……都算是出现过，而没有出现就是出现 \(0\) 次，显然更好求。

现在，我们预处理出每个数所有出现的位置，考虑一个数 \(x\) 对一次询问造成贡献需要满足什么条件。首先，区间需要包含所有 \(x\) 的位置。

如上图，也就是询问的左端点需小于L，右端点需大于R。除此之外，区间不能包含任何一个 \(x-1\) 的位置。

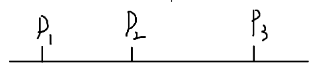
也就是区间的左端点和右端点同时在相邻两个位置之间。

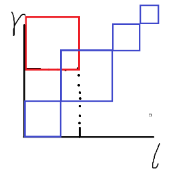
最后每个数可以产生贡献的区间就变成了一个矩形（红）和一堆矩形（蓝）的交。矩形的交也是矩形，并且总共只有 \(O(n)\) 个矩形造成贡献，我们枚举 \(x\) ，把这些矩形求出来。那么问题就转化为多次矩形加 \(1\) 和多次单点求值，直接扫描线扫一遍就可以了。

P1502 窗口的星星 - 洛谷

平面内有 \(n\) 个星星，每个星星有一个亮度值，求一个长宽分别为 \(H\),\(W\) 的窗户能够框柱最大的亮度和。

sol：

因为窗户的长宽都是确定的，所以窗户的右上角就可以确定这个窗户。首先还是反演，考虑一个星星的坐标是 \((x,y)\) ，那右上角在 \((x,y)\) 向上向右分别拓展 \(H\) 和 \(W\) 范围内。所以我们只需要做 \(n\) 次矩形加，每次求全局最大值即可。