DS 优化建图
题单来一个(不是我组的)。
CF786B Legacy
板子题先来一个:\(u \to v, u \to [l, r], [l, r] \to v\) 连边,求最短路。
考虑将区间 \([l, r]\) 用线段树的方式拆成 \(\log n\) 个小区间,然后将 \(u\) 分别连向这些区间即可。
然后你会发现线段树的父节点和儿子节点是可到达的,所以也要连边。
由于有 \(u \to [l, r], [l, r] \to v\),连边的方向相反,所以要在两棵线段树上完成,且两棵树的连边方向不一样(一个是从根往下,另一个是从叶子往上)。
还有一点就是说两棵树的叶子其实代表一个点,所以也要互相连边权为 \(0\) 的边。
注意:一定要算清楚一共有多少个点!!!
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define PII pair<int, ll>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define ll long long
using namespace std;
const int N = 1e6 + 5; const ll INF = (ll)1e18 + 5;
int n, Q, S, vis[N]; vector<PII > G[N]; vector<int> node; ll dis[N];
struct Node {
int id; ll val;
inline bool operator < (const Node & t) const { return val > t.val; }
}; priority_queue<Node> q;
struct Segment_Tree {
#define lc (p << 1)
#define rc (p << 1 | 1)
#define mid ((tr[p].l + tr[p].r) >> 1)
int x; struct Tree { int l, r; } tr[N << 2];
inline bool In(int p, int l, int r) { return l <= tr[p].l && tr[p].r <= r; }
void build(int p, int l, int r) {
tr[p].l = l, tr[p].r = r;
if (p > 1) {
if (x == n) G[(p >> 1) + x].pb(mp(p + x, 0));
else G[p + x].pb(mp((p >> 1) + x, 0));
} if (l == r) G[p + x].pb(mp(l, 0)), G[l].pb(mp(p + x, 0));
else build(lc, l, mid), build(rc, mid + 1, r);
} void query(int p, int l, int r) {
if (In(p, l, r)) return node.push_back(x + p);
if (l <= mid) query(lc, l, r);
if (r > mid) query(rc, l, r);
}
#undef lc
#undef rc
#undef mid
} SGT[2];
inline void Dijkstra() {
_for (i, 1, n * 9) dis[i] = INF, vis[i] = 0; q.push((Node){S, 0}), dis[S] = 0;
while (q.size()) {
int u = q.top().id; q.pop();
if (vis[u]) continue; vis[u] = 1;
for (PII v : G[u]) if (dis[v.fi] > dis[u] + v.se) dis[v.fi] = dis[u] + v.se, q.push((Node){v.fi, dis[v.fi]});
}
} int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> Q >> S, SGT[0].x = n, SGT[1].x = n * 5, SGT[0].build(1, 1, n), SGT[1].build(1, 1, n); int op, x, y, z, w;
while (Q -- ) {
cin >> op >> x >> y >> z;
if (op == 1) G[x].pb(mp(y, z));
else if (op == 2) {
cin >> w, node.clear(), SGT[0].query(1, y, z);
for (int u : node) G[x].pb(mp(u, w));
} else if (op == 3) {
cin >> w, node.clear(), SGT[1].query(1, y, z);
for (int u : node) G[u].pb(mp(x, w));
}
} Dijkstra();
_for (i, 1, n) cout << (dis[i] == INF ? - 1 : dis[i]) << " "; cout << "\n";
return 0;
}
P6348 [PA 2011] Journeys
再来一个板子:\([l_1, r_1] \to [l_2, r_2]\) 连边,求最短路。
有两种连边方式:
-
暴力建边:分别拆成 \(\log n\) 个区间,总共 \(\log^2 n\) 条边。
-
建虚点:\([l_1, r_1] \to A \to B \to [l_2, r_2]\),共 \(2 \log n\) 条边。
显然后者更优。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define PII pair<int, ll>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
#define ll long long
using namespace std;
const int N = 1e7 + 5, INF = 1e9 + 5;
int n, Q, S, vis[N], dis[N]; vector<PII > G[N]; vector<int> node1, node2;
struct Node {
int id; ll val;
inline bool operator < (const Node & t) const { return val > t.val; }
}; priority_queue<Node> q;
struct Segment_Tree {
#define lc (p << 1)
#define rc (p << 1 | 1)
#define mid ((tr[p].l + tr[p].r) >> 1)
int x; struct Tree { int l, r; } tr[N << 2];
inline bool In(int p, int l, int r) { return l <= tr[p].l && tr[p].r <= r; }
void build(int p, int l, int r) {
tr[p].l = l, tr[p].r = r;
if (p > 1) {
if (x == n + 4 * Q) G[p + x].pb(mp(p / 2 + x, 0));
else G[p / 2 + x].pb(mp(p + x, 0));
} if (l == r) G[p + x].pb(mp(l + Q * 4, 0)), G[l + Q * 4].pb(mp(p + x, 0));
else build(lc, l, mid), build(rc, mid + 1, r);
} void query(int p, int l, int r, vector<int> & node) {
if (In(p, l, r)) return node.push_back(x + p);
if (l <= mid) query(lc, l, r, node);
if (r > mid) query(rc, l, r, node);
}
#undef lc
#undef rc
#undef mid
} SGT[2];
inline void Dijkstra() {
_for (i, 1, n * 9 + 4 * Q) dis[i] = INF, vis[i] = 0; q.push((Node){S, 0}), dis[S] = 0;
while (q.size()) {
int u = q.top().id; q.pop();
if (vis[u]) continue; vis[u] = 1;
for (PII v : G[u]) if (dis[v.fi] > dis[u] + v.se) dis[v.fi] = dis[u] + v.se, q.push((Node){v.fi, dis[v.fi]});
}
} int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> Q >> S, S += 4 * Q, SGT[0].x = n + Q * 4, SGT[1].x = n * 5 + Q * 4, SGT[0].build(1, 1, n), SGT[1].build(1, 1, n); int x, y, z, w, u = - 1, v = 0;
_for (_, 1, Q) {
cin >> w >> x >> y >> z, node1.clear(), SGT[0].query(1, w, x, node1), node2.clear(), SGT[1].query(1, y, z, node2), u += 2, v += 2;
for (int i : node1) G[i].pb(mp(u, 0)); G[u].pb(mp(v, 1));
for (int i : node2) G[v].pb(mp(i, 0)); node1.clear(), SGT[0].query(1, y, z, node1), node2.clear(), SGT[1].query(1, w, x, node2), u += 2, v += 2;
for (int i : node1) G[i].pb(mp(u, 0)); G[u].pb(mp(v, 1));
for (int i : node2) G[v].pb(mp(i, 0));
} Dijkstra();
_for (i, 1 + 4 * Q, n + 4 * Q) cout << dis[i] << "\n";
return 0;
}
P5344 【XR-1】逛森林
第一想法是树剖 + 线段树优化建图,但你注意到会有 \(\ge m \log^2 n\) 个点,空间和时间都爆炸了。
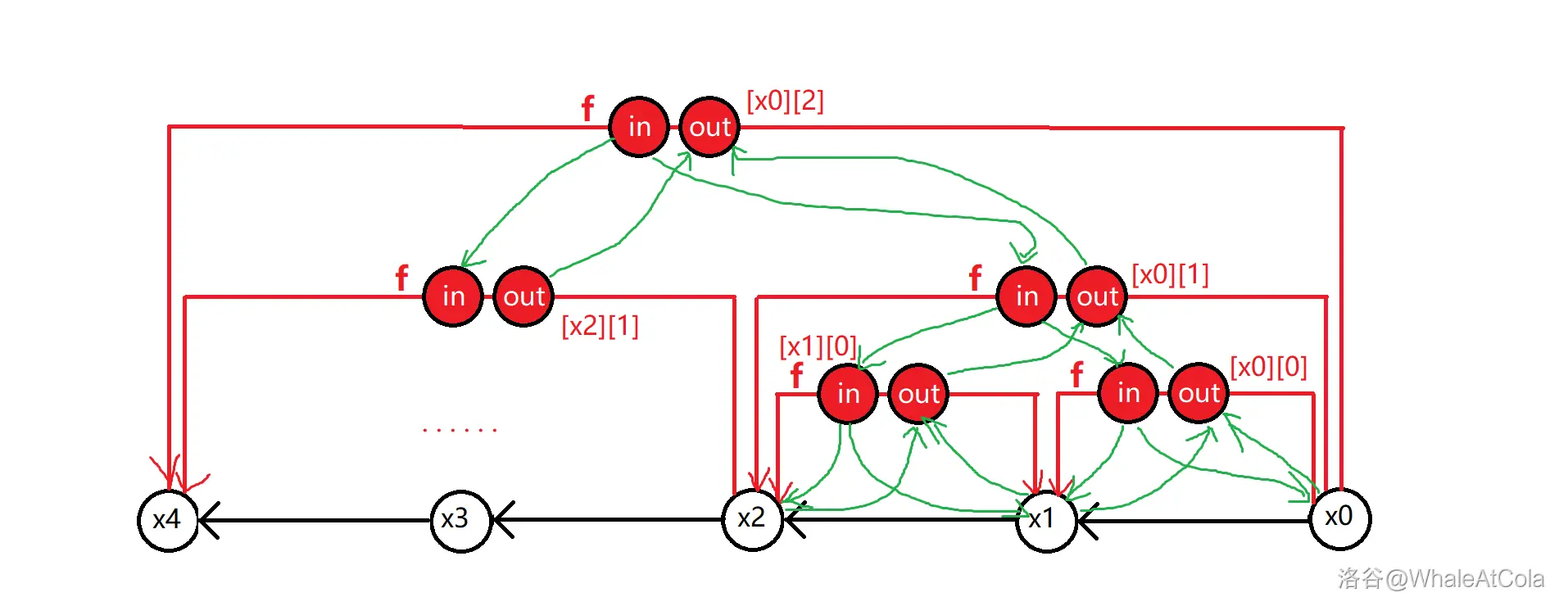
具体的,设 \(UP_{u, i}\) 表示点 \(u\) 向上跳 \(2^i\) 步到达的点。那么我们可以把一个点拆为入点和出点,连接 \(UP_{u, i}\) 和 \(UP_{u, i - 1}\) 的入点和出点即可。
这样的点数是多少呢?首先 \(UP_{u, i}\) 有 \(n \log n\) 个点,每个点都拆为入点和出点。对于一条边都建两个虚点。所以总点数 \(n + 2 n \log n + 2m\),边数 \(\le 2 n \log n + 5 m \log n\),优于树剖建图。
放一张图(贺的洛谷题解):
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define _all(i, a, b) for (int i = (a); i >= (b); i -- )
#define PII pair<int, int>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
using namespace std;
const int N = 5e4 + 5, M = 1e6 + 5, V = 16, K = N + 2 * N * V + 2 * M, INF = 1e9 + 5;
int n, Q, L, qcnt, S, ncnt, vis[K], dep[N], UP[N][V], in[N][V], out[N][V], dis[K]; vector<PII > G[K]; vector<int> Tr[N];
struct OP2 { int u1, v1, u2, v2, w; } tmp[M];
struct DSU {
int fa[N];
inline void init() { iota(fa + 1, fa + n + 1, 1); }
int find(int u) { return fa[u] == u ? u : fa[u] = find(fa[u]); }
inline bool con(int u, int v) { return find(u) == find(v); }
inline void merge(int u, int v) { fa[find(u)] = find(v); }
} DSU;
struct Node {
int id, val;
inline bool operator < (const Node & t) const { return val > t.val; }
}; priority_queue<Node> q;
inline void Dijkstra(int S) {
_for (i, 1, ncnt) vis[i] = 0, dis[i] = INF; q.push((Node){S, dis[S] = 0});
while (q.size()) {
int u = q.top().id; q.pop();
if (vis[u]) continue; vis[u] = 1;
for (PII v : G[u]) if (v.fi && dis[v.fi] > dis[u] + v.se) q.push((Node){v.fi, dis[v.fi] = dis[u] + v.se});
}
} void dfs(int u, int fa) {
dep[u] = dep[fa] + 1, UP[u][0] = fa, in[u][0] = ++ ncnt, G[ncnt].pb(mp(u, 0)), G[ncnt].pb(mp(fa, 0)), out[u][0] = ++ ncnt, G[u].pb(mp(ncnt, 0)), G[fa].pb(mp(ncnt, 0));
_for (i, 1, L) UP[u][i] = UP[UP[u][i - 1]][i - 1], in[u][i] = ++ ncnt, G[ncnt].pb(mp(in[u][i - 1], 0)), G[ncnt].pb(mp(in[UP[u][i - 1]][i - 1], 0)), out[u][i] = ++ ncnt, G[out[u][i - 1]].pb(mp(ncnt, 0)), G[out[UP[u][i - 1]][i - 1]].pb(mp(ncnt, 0));
for (int v : Tr[u]) if (v ^ fa) dfs(v, u);
} inline void add_path_out(int u, int v, int o) {
if (dep[u] < dep[v]) swap(u, v); G[v].pb(mp(o, 0));
_all (i, L, 0) if (dep[UP[u][i]] >= dep[v]) G[out[u][i]].pb(mp(o, 0)), u = UP[u][i];
if (u ^ v) { _all (i, L, 0) if (UP[u][i] ^ UP[v][i]) G[out[u][i]].pb(mp(o, 0)), G[out[v][i]].pb(mp(o, 0)), u = UP[u][i], v = UP[v][i]; G[out[u][0]].pb(mp(o, 0)); }
} inline void add_path_in(int u, int v, int o) {
if (dep[u] < dep[v]) swap(u, v); G[o].pb(mp(v, 0));
_all (i, L, 0) if (dep[UP[u][i]] >= dep[v]) G[o].pb(mp(in[u][i], 0)), u = UP[u][i];
if (u ^ v) { _all (i, L, 0) if (UP[u][i] ^ UP[v][i]) G[o].pb(mp(in[u][i], 0)), G[o].pb(mp(in[v][i], 0)), u = UP[u][i], v = UP[v][i]; G[o].pb(mp(in[u][0], 0)); }
} int main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> Q >> S, ncnt = n, L = (int)floor(log2(n)), DSU.init(); int op, u1, v1, u2, v2, w;
while (Q -- ) {
cin >> op >> u1 >> v1;
if (op == 1) {
cin >> u2 >> v2 >> w;
if (DSU.con(u1, v1) && DSU.con(u2, v2)) tmp[ ++ qcnt] = (OP2){u1, v1, u2, v2, w};
} else {
cin >> w;
if ( ! DSU.con(u1, v1)) Tr[u1].pb(v1), Tr[v1].pb(u1), G[u1].pb(mp(v1, w)), G[v1].pb(mp(u1, w)), DSU.merge(u1, v1);
}
} _for (i, 1, n) if ( ! dep[i]) dfs(i, 0);
_for (i, 1, qcnt) add_path_out(tmp[i].u1, tmp[i].v1, ++ ncnt), add_path_in(tmp[i].u2, tmp[i].v2, ++ ncnt), G[ncnt - 1].pb(mp(ncnt, tmp[i].w)); Dijkstra(S);
_for (i, 1, n) cout << (dis[i] == INF ? - 1 : dis[i]) << " "; cout << "\n";
return 0;
}
P3783 [SDOI2017] 天才黑客
考虑边转成点。每条边拆成入点和出点。连边的时候枚举一下原图上的点,然后连接相邻边的入点和出点即可。
这样连边边数最高可能达到 \(O(m^2)\),无法通过。
考虑两条边的边权实际上是在 trie 树上的 LCA 的深度。而对于每个点来说,假设其相邻的边有 \(x\) 条,那么 LCA 的可能位置最多有 \(x\) 个(根据虚树的一些理论)。按照 dfn 序排序后,还有一个重要性质:
所以说如果一段区间包含了最小值的边,那么其他边是无意义的(最短路)。
考虑前缀后缀优化连边。具体的,对于每一条边开四个点 \(\text{pre_in}, \text{pre_out}, \text{suf_in}, \text{suf_out}\),分别表示前缀入点、前缀出点、后缀入点、后缀出点。然后就是前缀后缀相邻的连一些边,相邻的出点向入点连一些边,入点出点分别向原来的边连边。
这样的边数是 \(O(m)\) 级别的。时间复杂度 \(O(m \log m)\),瓶颈在于 sort 和 Dijkstra。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define _all(i, a, b) for (int i = (a); i >= (b); i -- )
#define ll long long
#define PII pair<int, int>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
using namespace std;
const int N = 5e4 + 5, M = 2e4 + 5, K = 10 * N; const ll INF = (ll)1e18 + 5;
int n, m, k, S, ncnt, dfn_cnt, vis[K], pre_in[N], pre_out[N], suf_in[N], suf_out[N], sz[M], son[M], dep[M], top[M], dfn[M], rk[M], fa[M]; vector<int> in[N], out[N], Tr[M]; vector<PII > ee, G[K]; ll dis[K], ans[K];
struct Node {
int id; ll val;
inline bool operator < (const Node & t) const { return val > t.val; }
}; priority_queue<Node> q;
struct Edge { int a, b, c, d; } e[N];
void dfs1(int u) {
sz[u] = 1, son[u] = - 1;
for (int v : Tr[u]) if (v ^ fa[u]) {
fa[v] = u, dep[v] = dep[u] + 1, dfs1(v), sz[u] += sz[v];
if ( ! ~ son[u] || sz[son[u]] < sz[v]) son[u] = v;
}
} void dfs2(int u, int Top) {
rk[dfn[u] = ++ dfn_cnt] = u, top[u] = Top;
if ( ~ son[u]) dfs2(son[u], Top);
for (int v : Tr[u]) if (v ^ son[u] && v ^ fa[u]) dfs2(v, v);
} inline int lca(int u, int v) {
int U = top[u], V = top[v];
while (U ^ V) {
if (dep[U] >= dep[V]) u = fa[U];
else v = fa[V]; U = top[u], V = top[v];
} return (dep[u] < dep[v] ? u : v);
} inline void Dijkstra() {
_for (i, 0, ncnt) dis[i] = INF, vis[i] = 0; q.push((Node){S, dis[S] = 0});
while (q.size()) {
int u = q.top().id; q.pop();
if (vis[u]) continue; vis[u] = 1;
for (PII v : G[u]) if (dis[v.fi] > dis[u] + v.se) q.push((Node){v.fi, dis[v.fi] = dis[u] + v.se});
}
} inline void clear() {
S = dfn_cnt = 0, ncnt = m << 1;
_for (i, 0, K - 1) G[i].clear();
_for (i, 1, n) in[i].clear(), out[i].clear(), ans[i] = INF;
_for (i, 1, k) Tr[i].clear();
} inline void solve() {
cin >> n >> m >> k, clear(); int u, v, w;
_for (i, 1, m) cin >> e[i].a >> e[i].b >> e[i].c >> e[i].d, out[e[i].a].pb(i), in[e[i].b].pb(i), G[i].pb(mp(i + m, e[i].c));
_for (i, 2, k) cin >> u >> v >> w, Tr[u].pb(v); dfs1(1), dfs2(1, 1); // trie
_for (i, 1, m) if (e[i].a == 1) G[S].pb(mp(i, 0));
_for (i, 1, n) {
ee.clear();
for (int j : in[i]) ee.pb(mp(e[j].d, j + m));
for (int j : out[i]) ee.pb(mp(e[j].d, j)); sort(ee.begin(), ee.end(), [&] (PII x, PII y) { return dfn[x.fi] < dfn[y.fi]; }); // build virtual tree
_for (j, 0, (int)ee.size() - 1) pre_in[j] = ++ ncnt, pre_out[j] = ++ ncnt, suf_in[j] = ++ ncnt, suf_out[j] = ++ ncnt;
_for (j, 0, (int)ee.size() - 2) G[pre_in[j + 1]].pb(mp(pre_in[j], 0)), G[pre_out[j]].pb(mp(pre_out[j + 1], 0)), G[suf_in[j]].pb(mp(suf_in[j + 1], 0)), G[suf_out[j + 1]].pb(mp(suf_out[j], 0)), G[suf_out[j + 1]].pb(mp(pre_in[j], w = dep[lca(ee[j].fi, ee[j + 1].fi)])), G[pre_out[j]].pb(mp(suf_in[j + 1], w));
_for (j, 0, (int)ee.size() - 1) {
if (ee[j].se <= m) G[suf_in[j]].pb(mp(ee[j].se, 0)), G[pre_in[j]].pb(mp(ee[j].se, 0));
else G[ee[j].se].pb(mp(suf_out[j], 0)), G[ee[j].se].pb(mp(pre_out[j], 0));
}
} Dijkstra();
_for (i, 1, m) ans[e[i].b] = min(ans[e[i].b], dis[i + m]);
_for (i, 2, n) cout << ans[i] << "\n";
} signed main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
int T; cin >> T; while (T -- ) solve();
return 0;
}
P3588 [POI 2015] PUS
较为简单的题目。考虑将大于关系转化为连边。线段树优化连边,总共 \(\sum k \log n\) 条边。
如果连成环了且环上边权和非零,一定无解。转化为 DAG 上 DP。复杂度 \(O((n + \sum k) \log n)\)。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define _all(i, a, b) for (int i = (a); i >= (b); i -- )
#define ll long long
#define ld long double
#define PII pair<int, int>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
using namespace std;
const int N = 3e5 + 5, K = N * 10;
int n, ncnt, s, m, col[K], flag[K], in_deg[K], vis[K], val[K]; vector<PII > G[K]; vector<int> node; queue<int> q;
inline void chkmin(int & x, int y) { x = x < y ? x : y; }
inline void NIE() { cout << "NIE\n", exit(0); }
struct Segment_Tree {
#define lc (p << 1)
#define rc (p << 1 | 1)
#define mid ((tr[p].l + tr[p].r) >> 1)
struct Tree { int l, r; } tr[N << 2];
inline int len(int p) { return tr[p].r - tr[p].l + 1; }
inline bool In(int p, int l, int r) { return l <= tr[p].l && tr[p].r <= r; }
inline int id(int p) { return len(p) == 1 ? tr[p].l : p + n; }
void build(int p, int l, int r) {
tr[p].l = l, tr[p].r = r;
if (p > 1) G[id(p >> 1)].pb(mp(id(p), 0)), in_deg[id(p)] ++ ;
if (l ^ r) build(lc, l, mid), build(rc, mid + 1, r);
} void query(int p, int l, int r, vector<int> & vec) {
if (l > r) return ;
if (In(p, l, r)) return vec.push_back(id(p));
if (l <= mid) query(lc, l, r, vec);
if (r > mid) query(rc, l, r, vec);
}
#undef lc
#undef rc
#undef mid
} SGT;
void dfs(int u) {
vis[u] = col[u] = 1;
for (PII v : G[u]) {
if (vis[v.fi]) NIE();
if ( ! col[v.fi]) dfs(v.fi);
} vis[u] = 0;
} signed main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> s >> m, ncnt = 5 * n, SGT.build(1, 1, n); int l, r, k, x, lst;
while (s -- ) {
cin >> x >> k;
if (k < 1 || k > 1e9 || (val[x] && val[x] ^ k)) NIE(); val[x] = k, flag[x] = 1;
} while (m -- ) {
cin >> l >> r >> k, lst = l - 1, ncnt += 2, G[ncnt - 1].pb(mp(ncnt, 1)), in_deg[ncnt] ++ , node.clear();
while (k -- ) cin >> x, SGT.query(1, lst + 1, x - 1, node), G[x].pb(mp(ncnt - 1, 0)), in_deg[ncnt - 1] ++ , lst = x; SGT.query(1, lst + 1, r, node);
for (int i : node) G[ncnt].pb(mp(i, 0)), in_deg[i] ++ ;
} _for (i, 1, ncnt) { if ( ! col[i]) dfs(i); val[i] = val[i] ? val[i] : 1e9; }
_for (i, 1, ncnt) if ( ! in_deg[i]) q.push(i);
while (q.size()) {
int u = q.front(); q.pop();
for (PII v : G[u]) {
if (flag[v.fi] && val[u] - v.se < val[v.fi]) NIE(); chkmin(val[v.fi], val[u] - v.se);
if (val[v.fi] < 1) NIE();
if ( ! ( -- in_deg[v.fi])) q.push(v.fi);
}
} cout << "TAK\n";
_for (i, 1, n) cout << val[i] << " "; cout << "\n";
return 0;
}
P7215 [JOISC 2020] 首都 / AT_joisc2020_j 首都 (Capital City)
考虑如果两个属于 \(i\) 的点的路径上含有属于 \(j\) 的点,则连边 \(i \to j\)。这样连边后缩点,一个强联通分量想要成为答案,必然要将强连通分量中所有点都归为一类(原因显然),操作次数是 点的个数减一。
注意到缩点之后是 DAG,如果有连边 \(x \to y\)(\(x, y\) 都为强连通分量),那么如果想让 \(x\) 中点成为答案,得将 \(y\) 中点 merge 到 \(x\) 中才可以。所以选择 \(y\) 显然优于选 \(x\)。
所以答案为 所有出度为 \(0\) 的强连通分量点的个数 \(\min\) 减去 \(1\)。
树剖 + 线段树优化建图。复杂度 \(O(n \log^2 n)\)。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define _all(i, a, b) for (int i = (a); i >= (b); i -- )
#define ll long long
#define pb push_back
using namespace std;
const int N = 1e6 + 5, INF = 2e9 + 5;
int n, m, ans = INF, dfn_cnt, ncnt, scc, Top, stk[N], bel[N], in_stack[N], tot[N], low[N], sz[N], son[N], vis[N], dep[N], top[N], dfn[N], rnk[N], fa[N], col[N], out_deg[N]; vector<int> Tr[N], C[N], G[N];
inline void chkmin(int & x, int y) { x = x < y ? x : y; }
inline void chkmax(int & x, int y) { x = x > y ? x : y; }
struct Segment_Tree {
#define lc (p << 1)
#define rc (p << 1 | 1)
#define mid ((tr[p].l + tr[p].r) >> 1)
struct Tree { int l, r; } tr[N << 2];
inline int len(int p) { return tr[p].r - tr[p].l + 1; }
inline bool In(int p, int l, int r) { return l <= tr[p].l && tr[p].r <= r; }
inline int id(int p) { return len(p) == 1 ? col[rnk[tr[p].l]] : p + m; }
void build(int p, int l, int r) {
tr[p].l = l, tr[p].r = r, vis[id(p)] = 1;
if (p > 1) G[id(p >> 1)].pb(id(p));
if (l == r) return ; build(lc, l, mid), build(rc, mid + 1, r);
} void query(int p, int l, int r, int k) {
if (l > r) return ;
if (In(p, l, r)) return G[k].pb(id(p)), void();
if (l <= mid) query(lc, l, r, k);
if (r > mid) query(rc, l, r, k);
}
#undef lc
#undef rc
#undef mid
} SGT;
void dfs1(int u) {
sz[u] = 1, son[u] = - 1;
for (int v : Tr[u]) if (v ^ fa[u]) {
fa[v] = u, dep[v] = dep[u] + 1, dfs1(v), sz[u] += sz[v];
if ( ! ~ son[u] || sz[son[u]] < sz[v]) son[u] = v;
}
} void dfs2(int u, int Top) {
rnk[dfn[u] = ++ dfn_cnt] = u, top[u] = Top;
if ( ~ son[u]) dfs2(son[u], Top);
for (int v : Tr[u]) if (v ^ son[u] && v ^ fa[u]) dfs2(v, v);
} inline void add_edge(int u, int v, int k) {
int U = top[u], V = top[v];
while (U ^ V) {
if (dep[U] >= dep[V]) SGT.query(1, dfn[U], dfn[u], k), u = fa[U];
else SGT.query(1, dfn[V], dfn[v], k), v = fa[V]; U = top[u], V = top[v];
} SGT.query(1, min(dfn[u], dfn[v]), max(dfn[u], dfn[v]), k);
} inline void Tarjan(int u) {
dfn[u] = low[u] = ++ dfn_cnt, in_stack[u] = 1, stk[ ++ Top] = u;
for (int v : G[u]) {
if ( ! dfn[v]) Tarjan(v), low[u] = min(low[u], low[v]);
else if (in_stack[v]) low[u] = min(low[u], dfn[v]);
} if (low[u] == dfn[u] && vis[u]) {
scc ++ ;
do { bel[stk[Top]] = scc, in_stack[stk[Top]] = 0, tot[scc] += stk[Top] <= m; } while (stk[Top -- ] ^ u);
}
}
signed main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n >> m, ncnt = m + 4 * n; int u, v;
_for (i, 1, m) vis[i] = 1;
_for (i, 2, n) cin >> u >> v, Tr[u].pb(v), Tr[v].pb(u); dfs1(1), dfs2(1, 1);
_for (i, 1, n) cin >> col[i], C[col[i]].pb(i); SGT.build(1, 1, n);
_for (i, 1, m) {
sort(C[i].begin(), C[i].end(), [&] (int x, int y) { return dfn[x] < dfn[y]; });
_for (j, 0, (int)C[i].size() - 2) add_edge(C[i][j], C[i][j + 1], i);
} dfn_cnt = 0;
_for (i, 1, n) dfn[i] = 0;
_for (i, 1, ncnt) if (vis[i] && ! dfn[i]) Tarjan(i);
_for (u, 1, ncnt) for (int v : G[u]) if (bel[u] ^ bel[v]) out_deg[bel[u]] ++ ;
_for (i, 1, scc) if ( ! out_deg[i]) chkmin(ans, tot[i]); cout << ans - 1 << "\n";
return 0;
}
P5025 [SNOI2017] 炸弹
差一步啊 /ll。
考虑每个炸弹第一轮能引爆的点是一段区间,线段树优化连边。转化为每个点能到达的点数。
首先缩个点,转化为 DAG 问题。注意到如果是一般 DAG 这个问题是 NPC 的。
但考虑到最后每个点的答案一定是区间,我们拓扑的时候只需记录能到达的 \(l, r\) 即可。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define ll long long
#define pb push_back
#define PII pair<int, int>
#define mp make_pair
using namespace std;
const int N = 3e6 + 5, P = 1e9 + 7; const ll INF = (ll)1e18 + 5;
int n, Ans, dfn_cnt, ncnt, scc, top, ansl[N], ansr[N], vis[N], ans[N], stk[N], bel[N], in_stack[N], low[N], dfn[N], f[N], in_deg[N]; ll x[N], r[N]; vector<int> vec[N], G[N], G2[N]; map<PII, int> occur; queue<int> q;
inline int mul(int x, int y) { return 1ll * x * y % P; }
inline void Add(int & x, int y) { x = x + y >= P ? x + y - P : x + y; }
inline void chkmin(int & x, int y) { x = x < y ? x : y; }
inline void chkmax(int & x, int y) { x = x > y ? x : y; }
struct Segment_Tree {
#define lc (p << 1)
#define rc (p << 1 | 1)
#define mid ((tr[p].l + tr[p].r) >> 1)
struct Tree { int l, r; } tr[N << 2];
inline int len(int p) { return tr[p].r - tr[p].l + 1; }
inline bool In(int p, int l, int r) { return l <= tr[p].l && tr[p].r <= r; }
inline int id(int p) { return len(p) == 1 ? tr[p].l : p + n; }
void build(int p, int l, int r) {
tr[p].l = l, tr[p].r = r, vis[id(p)] = 1;
if (p > 1) G[id(p >> 1)].pb(id(p));
if (l ^ r) build(lc, l, mid), build(rc, mid + 1, r);
} void query(int p, int l, int r, int k) {
if (l > r) return ;
if (In(p, l, r)) return G[k].pb(id(p)), void();
if (l <= mid) query(lc, l, r, k);
if (r > mid) query(rc, l, r, k);
}
#undef lc
#undef rc
#undef mid
} SGT;
inline void Tarjan(int u) {
dfn[u] = low[u] = ++ dfn_cnt, in_stack[u] = 1, stk[ ++ top] = u;
for (int v : G[u]) {
if ( ! dfn[v]) Tarjan(v), low[u] = min(low[u], low[v]);
else if (in_stack[v]) low[u] = min(low[u], dfn[v]);
} if (low[u] == dfn[u]) {
scc ++ ;
do { bel[stk[top]] = scc, in_stack[stk[top]] = 0, f[scc] += stk[top] <= n, vec[scc].pb(stk[top]), chkmin(ansl[scc], stk[top] <= n ? stk[top] : N), chkmax(ansr[scc], stk[top] <= n ? stk[top] : - N); } while (stk[top -- ] ^ u);
}
}
signed main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n, SGT.build(1, 1, n); int L, R, mid, pos;
_for (i, 1, n) cin >> x[i] >> r[i], vis[i] = 1;
_for (i, 1, n) {
L = 1, R = i - 1, pos = i;
while (L <= R) {
mid = (L + R) >> 1;
if (x[mid] >= x[i] - r[i]) pos = mid, R = mid - 1;
else L = mid + 1;
} SGT.query(1, pos, i - 1, i), pos = i, L = i + 1, R = n;
while (L <= R) {
mid = (L + R) >> 1;
if (x[mid] <= x[i] + r[i]) pos = mid, L = mid + 1;
else R = mid - 1;
} SGT.query(1, i + 1, pos, i);
} _for (i, 1, 5 * n) ansl[i] = N, ansr[i] = - N;
_for (i, 1, 5 * n) if (vis[i] && ! dfn[i]) Tarjan(i);
_for (u, 1, 5 * n) for (int v : G[u]) if (vis[u] && vis[v] && bel[u] ^ bel[v] && ! occur[mp(bel[u], bel[v])]) occur[mp(bel[u], bel[v])] = 1, G2[bel[v]].pb(bel[u]), in_deg[bel[u]] ++ ;
_for (i, 1, scc) if ( ! in_deg[i]) q.push(i);
while (q.size()) {
int u = q.front(); q.pop();
for (int v : G2[u]) {
chkmin(ansl[v], ansl[u]), chkmax(ansr[v], ansr[u]);
if ( ! ( -- in_deg[v])) q.push(v);
}
} _for (i, 1, scc) for (int j : vec[i]) ans[j] = ansr[i] - ansl[i] + 1;
_for (i, 1, n) Add(Ans, mul(i, ans[i])); cout << Ans << "\n";
return 0;
}
CF1007D Ants
口胡了一下,不想写了。
考虑 2-sat,树剖 + 线段树优化建图即可。复杂度应该是 \(O(m \log^2 n)\)。
AT_arc069_d [ARC069F] Flags
线段树优化 2-sat 建图。
妈的 WA 了两个点调不过去了,不想调了。
Code
#include <bits/stdc++.h>
#define _for(i, a, b) for (int i = (a); i <= (b); i ++ )
#define _all(i, a, b) for (int i = (a); i >= (b); i -- )
#define ll long long
#define PII pair<int, int>
#define mp make_pair
#define fi first
#define se second
#define pb push_back
using namespace std;
const int N = 1e5 + 5;
int n, dfn_cnt, scc, top, x[N], y[N], stk[N], bel[N], in_stack[N], low[N], dfn[N]; PII a[N], b[N]; vector<int> G[N];
struct Segment_Tree {
#define lc (p << 1)
#define rc (p << 1 | 1)
#define mid ((tr[p].l + tr[p].r) >> 1)
int op, h; struct Tree { int l, r, val; } tr[N << 2];
inline int len(int p) { return tr[p].r - tr[p].l + 1; }
inline bool In(int p, int l, int r) { return l <= tr[p].l && tr[p].r <= r; }
inline int id(int p) { return len(p) == 1 ? tr[p].val : p + h; }
void build(int p, int l, int r) {
tr[p].l = l, tr[p].r = r, tr[p].val = op ? b[l].se : a[l].se + n;
if (p > 1) G[id(p >> 1)].pb(id(p));
if (l ^ r) build(lc, l, mid), build(rc, mid + 1, r);
} void query(int p, int l, int r, int k) {
if (l > r) return ;
if (In(p, l, r)) return G[k].pb(id(p)), void();
if (l <= mid) query(lc, l, r, k);
if (r > mid) query(rc, l, r, k);
}
#undef lc
#undef rc
#undef mid
} SGT[2];
inline void Tarjan(int u) {
dfn[u] = low[u] = ++ dfn_cnt, in_stack[u] = 1, stk[ ++ top] = u;
for (int v : G[u]) {
if ( ! dfn[v]) Tarjan(v), low[u] = min(low[u], low[v]);
else if (in_stack[v]) low[u] = min(low[u], dfn[v]);
} if (low[u] == dfn[u]) {
scc ++ ;
do { bel[stk[top]] = scc, in_stack[stk[top]] = 0; } while (stk[top -- ] ^ u);
}
}
#define mid ((l + r) >> 1)
inline bool valid(int v) {
int l, r, pos, posl, posr;
_for (i, 1, 10 * n) bel[i] = in_stack[i] = low[i] = dfn[i] = stk[i] = 0, G[i].clear(); dfn_cnt = scc = top = 0, SGT[0].build(1, 1, n), SGT[1].build(1, 1, n);
_for (i, 1, n) {
l = 1, r = n, pos = 0;
while (l <= r) a[mid].fi >= x[i] ? pos = mid, r = mid - 1 : l = mid + 1; l = 1, r = pos - 1, posl = pos; // x -> x
while (l <= r) a[mid].fi > x[i] - v ? posl = mid, r = mid - 1 : l = mid + 1; SGT[0].query(1, posl, pos - 1, i), l = pos + 1, r = n, posr = pos;
while (l <= r) a[mid].fi < x[i] + v ? posr = mid, l = mid + 1 : r = mid - 1; SGT[0].query(1, pos + 1, posr, i), l = 1, r = n, pos = 0;
while (l <= r) b[mid].fi >= y[i] ? pos = mid, r = mid - 1 : l = mid + 1; l = 1, r = n, posl = n + 1; // x -> y
while (l <= r) b[mid].fi > x[i] - v ? posl = mid, r = mid - 1 : l = mid + 1; l = posl, r = n, posr = 0;
while (l <= r) b[mid].fi < x[i] + v ? posr = mid, l = mid + 1 : r = mid - 1;
if (posl <= posr) {
if (pos < posl || pos > posr) SGT[1].query(1, posl, posr, i);
else SGT[1].query(1, posl, pos - 1, i), SGT[1].query(1, pos + 1, posr, i);
} l = 1, r = n, pos = 0;
while (l <= r) a[mid].fi >= x[i] ? pos = mid, r = mid - 1 : l = mid + 1; l = 1, r = n, posl = n + 1; // y -> x
while (l <= r) a[mid].fi > y[i] - v ? posl = mid, r = mid - 1 : l = mid + 1; l = posl, r = n, posr = 0;
while (l <= r) a[mid].fi < y[i] + v ? posr = mid, l = mid + 1 : r = mid - 1;
if (posl <= posr) {
if (pos < posl || pos > posr) SGT[0].query(1, posl, posr, i + n);
else SGT[0].query(1, posl, pos - 1, i + n), SGT[0].query(1, pos + 1, posr, i + n);
} l = 1, r = n, pos = 0;
while (l <= r) b[mid].fi >= y[i] ? pos = mid, r = mid - 1 : l = mid + 1; l = 1, r = pos - 1, posl = pos; // y -> y
while (l <= r) b[mid].fi > y[i] - v ? posl = mid, r = mid - 1 : l = mid + 1; SGT[1].query(1, posl, pos - 1, i + n), l = pos + 1, r = n, posr = pos;
while (l <= r) b[mid].fi < y[i] + v ? posr = mid, l = mid + 1 : r = mid - 1; SGT[1].query(1, pos + 1, posr, i + n);
} _for (i, 1, n << 1) if ( ! dfn[i]) Tarjan(i);
_for (i, 1, n) if (bel[i] == bel[i + n]) return 0; return 1;
} signed main() {
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
cin >> n; int l = 0, r = 1e9, ans = 0; SGT[0].op = 0, SGT[1].op = 1, SGT[0].h = 2 * n, SGT[1].h = 6 * n;
_for (i, 1, n) cin >> x[i] >> y[i], a[i] = mp(x[i], i), b[i] = mp(y[i], i); sort(a + 1, a + n + 1), sort(b + 1, b + n + 1);
while (l <= r) valid(mid) ? ans = mid, l = mid + 1 : r = mid - 1; cout << ans << "\n";
return 0;
}
P7452 [THUSC 2017] 换桌
线段树优化网络流建图。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号