机器学习实战 10-PCA

1 先备知识

1.1 一些统计学认识

方差: 用来描述样本偏离中心程度的量

协方差：用来描述两变量 X,Y 相互关系的量，协方差越大，对彼此影响越大，协方差等于0，两者独立

协方差矩阵：         

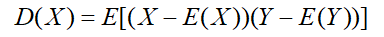
如果一组样本 y1,.......ym ,每个样本是 n 维行向量，则这组样本的协方差矩阵为：

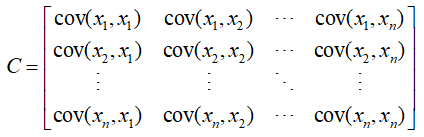
注意：矩阵中的 x1,......xn ,指的是上面m个样本的每一维值，则 xn 为 m 维列向量。

理解：由 m 个样本确定的 n 维空间，协方差矩阵的每一列表示的是所有维对某一维分别影响值（即相关性），描述这个 n 维空间。 协方差矩阵的对角线上为各个特征的方差。 

1.2 一些矩阵论知识

特征值和特征向量：

已经学习过很久的基础知识，说它们是矩阵中最重要的一环也不为过，但当我们学习各种骚操作计算这两值的时候，有没有想过它们是何意义，或者说有什么作用？再看公式，如下 ：

解释：A 将 α 做了一个变换，向量α在变换过后，方向没变，长度被拉伸 λ 倍。如图所示：

 

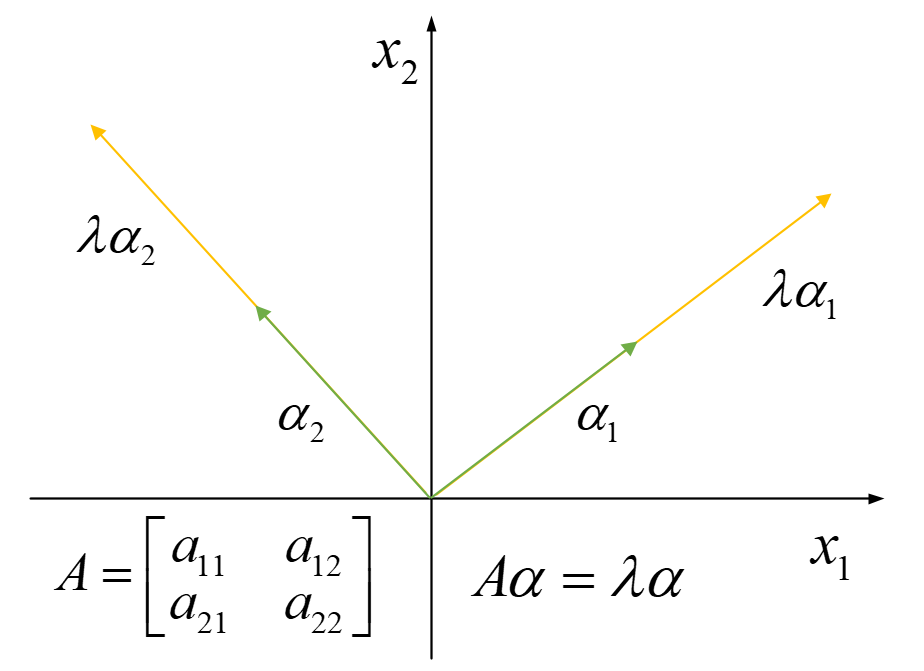
如果A是一个二维，则找到两个特征向量分别表示两个最具有代表性的方向，特征向量在此方向上经过A变换，方向不会改变，只会拉伸λ倍。这两个方向上包含矩阵A信息最多。

具体可参观：http://k.sina.com.cn/article_6367168142_17b83468e001005yrv.html

协方差矩阵对角化：

对称矩阵的一些性质：

    1. 实对称矩阵不同的特征值对应的特征向量必然正交

    2. 设 λ 是 k 重特征值，则 λ 对应必有 k 个线性无关的特征向量，并可将其对角化

由上可知一个 n*n 的对角矩阵一定可以找到 n 个线性无关的正交特征向量，正交阵 P 由这 n 个特征向量组成，则：

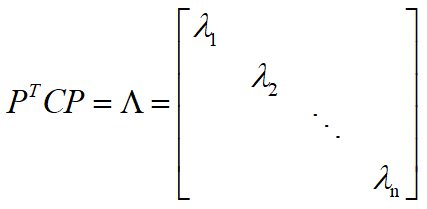
基变换：

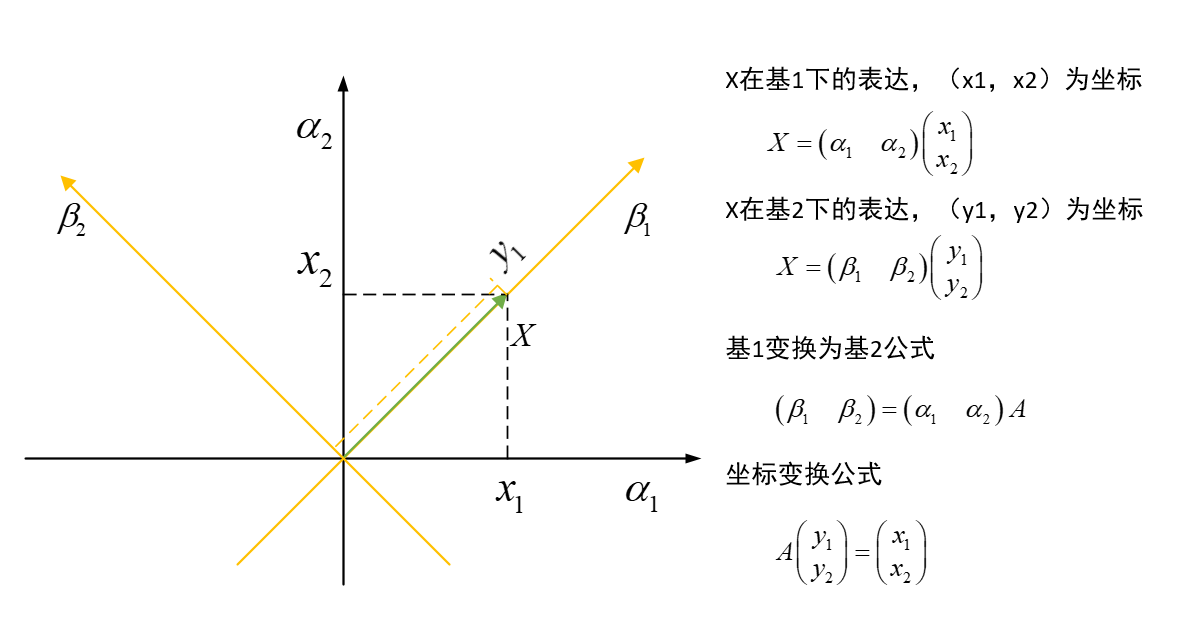
如图，在同一空间里，在不同基下坐标表达不同，图中向量在基变换以后，有一个方向的坐标已经变成0。其中，矩阵A则用来表示这个线性变换过程，称过渡矩阵。

2 PCA原理

2.1 特征降维

我们经常遇到一大批数据，千万级或者亿级别的数据，这些数据有很多个特征，但是这些特征很有可能有许多特征起到的作用是重复的（比如一种物体密度是一样的，那么这个物体的体积和重量这两个特征有重复），如果去除这些重复的，那么数据会苗条许多。另外有一部分维度的特征可能对于你本身想要研究的方向是噪声，去除他们，数据会更干净。所以，特征降维是一门重要技术，而PCA（主成分分析）就是一种特征降维方法。总结其作用如下：

    1. 去除噪声

    2. 降低算法计算复杂度，就是快一点

    3. 相对的要简洁易懂一点

2.2 PCA

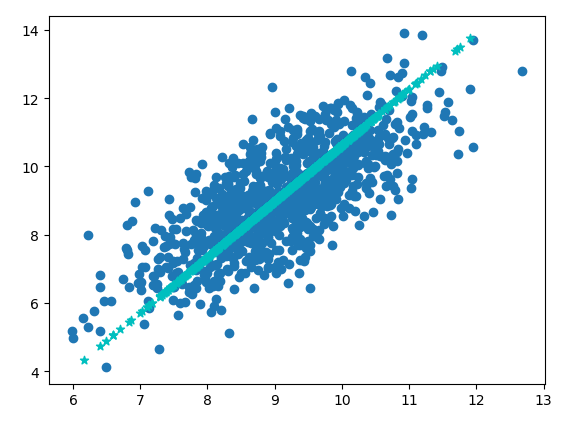
如图中是一组二维数据，但是其分布主要沿着图中星星这条直线上，所以我们可以将其投影到这条直线上进行研究，这样就从二维降到了一维。

理论分析（参考周志华《机器学习》）：

在正交属性空间中的样本点，用一个超平面（直线高阶推广）对所有样本恰当表达，这个超平面满足下面两个性质：

    • 最近重构性：样本到这个超平面的距离都足够近（损失最小）
    • 最大可分性：样本在这个超平面上的投影都尽可能分开（就是方差最大）

用这两个性质逆向推导，能够得到同样的条件：

其中 X 为 m 个 n 维特征的样本（已经中心化 ），W 为新的坐标系（n 维），取其中前 N （即对应于λ前 N 大的）维，经过变换，样本变为 N 维，从而达到降维目的。

算法过程：

注意：周老师书中的样本是横向排列，以下自我分析时，样本取的是纵向排列（日常分析数据时习惯使然）。

2.3 个人愚见

我们希望找到一个新的基向量组，原始数据在这些新基向量组下表示时，在每个属性上散布广，即方差大，且任何两个属性间的相关性为0。取出数据散布最广的前 N 个维度，将原始数据以新的基向量为参考坐标系表示出来，数据就能得到压缩。

上面 X^T·X 为样本的协方差矩阵，表示的各特征维度之间的相关关系，如果我们能使这个协方差矩阵对角化，那么除对角线之外的其他元素均为0，各维度之间无关，即属性间的相关性为0。问题就变成了我们如何使协方差矩阵对角化。以上已经给出对角化的方法，即求协方差的特征值和特征向量即可。

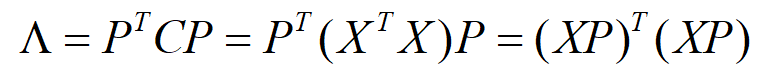
其中 P 为特征向量组成的正交阵，即为新基。 X 为 m 个 n 维特征的样本，原始基可以理解为 n 阶单位阵，默认坐标的表示方式为列向量。

这样我们在新基下的样本 Z 的协方差矩阵变为对角阵，各属性间毫无瓜葛，选取方差较大（即λ较大）的 N 维，便可得到降维后的数据，此数据保留大部分原数据信息。从这也能看出，在特征值大的特征向量方向保存信息多。

3 Python 实现

3.1 小试牛刀

 1 from numpy import *
 2 import matplotlib.pyplot as plt
 3 
 4 # 读取文件数据，并返回浮点数矩阵形式
 5 def loadDataSet(fileName,delim='\t'):
 6     fr=open(fileName)
 7     stringArr=[line.strip().split(delim) for line in fr.readlines()]
 8     datArr=[list(map(float,line)) for line in stringArr]
 9     return mat(datArr)
10 
11 # PCA
12 def pca(dataMat,topNfeat=9999999):
13     meanVals=mean(dataMat,axis=0)              # 按每列求取平均值
14     meanRemoved=dataMat-meanVals               # 中心化，即去除平均值
15     covMat=cov(meanRemoved,rowvar=0)           # 计算协方差矩阵
16     # covMat=meanRemoved.T*meanRemoved
17     eigVals,eigVects=linalg.eig(mat(covMat))   # 计算协方差矩阵的特征值和特征向量
18     eigValInd=argsort(eigVals)                 # 将特征值从小到大排列
19     eigValInd=eigValInd[:-(topNfeat+1):-1]     # 取前 N 大的特征值索引
20     redEigVects=eigVects[:,eigValInd]          # 保留最上面 N 个特征向量
21     lowDDataMat=meanRemoved*redEigVects        # 将数据转换为由 N 个特征向量构成的空间中
22     reconMat=(lowDDataMat*redEigVects.T)+meanVals
23     return lowDDataMat,reconMat
24 
25 dataMat=loadDataSet('testSet.txt')
26 print(dataMat.shape)
27 lowDMat,reconMat=pca(dataMat,1)
28 print(lowDMat.shape)
29 fig=plt.figure()
30 ax=fig.add_subplot(111)
31 ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0])
32 ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='*',c='c')
33 plt.show()

得到上面那张图，将数据都投影到星星线上了：

3.2 利用 PCA 对半导体制造数据降维

 1 from numpy import *
 2 import matplotlib.pyplot as plt
 3 
 4 # 读取文件数据，并返回浮点数矩阵形式
 5 def loadDataSet(fileName,delim='\t'):
 6     fr=open(fileName)
 7     stringArr=[line.strip().split(delim) for line in fr.readlines()]
 8     datArr=[list(map(float,line)) for line in stringArr]
 9     return mat(datArr)
10 
11 # PCA
12 def pca(dataMat,topNfeat=9999999):
13     meanVals=mean(dataMat,axis=0)              # 按每列求取平均值
14     meanRemoved=dataMat-meanVals               # 中心化，即去除平均值
15     covMat=cov(meanRemoved,rowvar=0)           # 计算协方差矩阵
16     # covMat=meanRemoved.T*meanRemoved
17     eigVals,eigVects=linalg.eig(mat(covMat))   # 计算协方差矩阵的特征值和特征向量
18     eigValInd=argsort(eigVals)                 # 将特征值从小到大排列
19     eigValInd=eigValInd[:-(topNfeat+1):-1]     # 取前 N 大的特征值索引
20     redEigVects=eigVects[:,eigValInd]          # 保留最上面 N 个特征向量
21     lowDDataMat=meanRemoved*redEigVects        # 将数据转换为由 N 个特征向量构成的空间中
22     reconMat=(lowDDataMat*redEigVects.T)+meanVals
23     return lowDDataMat,reconMat
24 
25 # 将数据中的 NaN 替换成平均值
26 def replaceNanWithMean():
27     datMat=loadDataSet('secom.data',' ')
28     numFeat=shape(datMat)[1]
29     # 遍历每一个特征值
30     for i in range(numFeat):
31         # 计算非 NaN 的平均值
32         meanVal=mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i])
33         # 填充平均值
34         datMat[nonzero(isnan(datMat[:,i].A))[0],i]=meanVal
35     return datMat
36 
37 dataMat=replaceNanWithMean()
38 meanVals = mean(dataMat, axis=0)  # 按每列求取平均值
39 meanRemoved = dataMat - meanVals  # 中心化，即去除平均值
40 covMat = cov(meanRemoved, rowvar=0)  # 计算协方差矩阵
41 eigVals, eigVects = linalg.eig(mat(covMat))  # 计算协方差矩阵的特征值和特征向量
42 print(eigVals)
43 
44 fig=plt.figure()
45 ax=fig.add_subplot(121)
46 ax.plot(eigVals[:20],marker='*',c='g')
47 bx=fig.add_subplot(122)
48 bx.pie(eigVals,autopct='%1.1f',radius=1.3)
49 plt.show()
View Code

最后得到下面关于方差百分比的图：

 

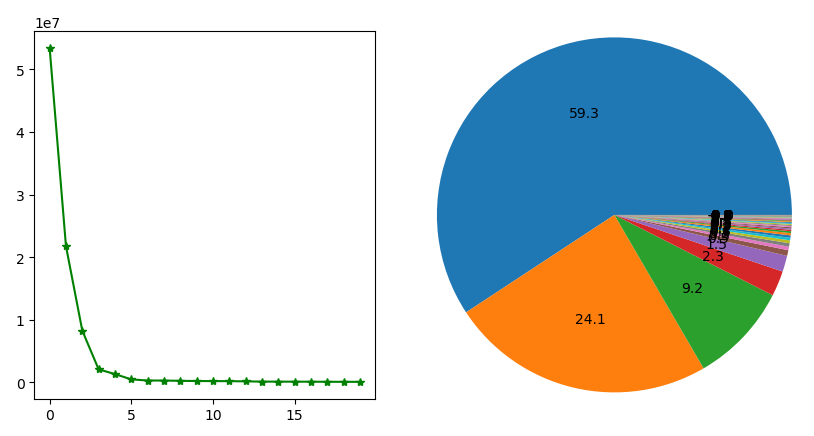
结论：可以发现半导体590个特征中，前6个主成分覆盖了数据的96.8%的方差，如果去除后面584个特征，将能实现很好的压缩，数据简洁，噪声也被去除，更易处理。

参考文献：

  1. 周志华 《机器学习》，peter 《机器学习实战》

  2. PCA的数学原理(非常值得阅读)！！！ https://blog.csdn.net/xiaojidan2011/article/details/11595869

  3. 看完这篇图解 PCA，面试再也不担心  https://zhuanlan.zhihu.com/p/44371812

 

posted @ 2019-06-04 20:47  滇红88号  阅读(246)  评论(0)  编辑  收藏  举报