5814. 【NOIP提高A组模拟2018.8.14】 树
###Description
梦游中的你来到了一棵 N 个节点的树上. 你一共做了 Q 个梦, 每个梦需要你从点 u 走到 点 v 之后才能苏醒, 由于你正在梦游, 所以每到一个节点后,你会在它连出去的边中等概率地 选择一条走过去, 为了确保第二天能够准时到校, 你要求出每个梦期望经过多少条边才能苏 醒. 为了避免精度误差, 你要输出答案模10^9 + 7的结果.
###Input
第一行两个整数分别代表 N 和 Q. 接下来 N-1 行, 每行两个整数 u, v 代表树中的一条边. 接下来 Q 行, 每行两个整数代表询问的 u,v.
###Output
一共 Q 行, 每行一个整数代表答案
###Sample Input
4 2
1 2
2 3
3 4
1 4
3 4
###Sample Output
9
5
###Data Constraint
对于 20%的数据, N <= 10.
对于 40%的数据, N <= 1000.
另有 20%的数据, 保证给定的树是一条链.
对于 100%的数据, N <= 100000, Q <= 100000.
###Hint
###题解:
首先,我们仔细看题。
仔细看,再仔细看。
然而,你没有熟练掌握一些概率或期望的知识,真的很难解释题意。
一般期望题的样例解释大概都是这样:有1/a概率1步到达,有1/b概率3步到达,有1/c概率5步到达……我们可以计算出期望d步到达。
我们看看这段东西,是某栋爷的解释。
然后再加上期望的定义:花费*概率
这样子自己手玩玩不就可以比较好地推出样例了吗?
但是,有一个问题,一般期望不是实数吗?
这个你先不管它,因为出题人认为做题人太强了,一眼就看到了正解。
所以,数据就变这样了。
不多说废话。(已经再解释期望时说了很多了)
我们看题——由于是从x走到y。
那么必然有一个lca。然后行走路径变成x→lca。lca→y。
变成一上一下。
那么我们就维护两个东西:
f[i]表示当前点i走到它父亲节点的期望。
g[i]表示当前点i从它父亲走回来的期望。
f就很好转移:
deg表示当前点的出度。
那么期望即为:花费* 概率= 1 *(1/dep[v])
上面的式子表示当前到v这个点。
走到父亲的期望+
返回v的儿子后再走回来v这个点再走到父亲的期望。
很好看,对吧?
我们可以考虑化简:两边同乘deg[v],移一下项,即可得到:
再看看g。g就有点麻烦:
fa表示v的父亲
表示为当前到fa这个点。
直接走到v的期望+
走到fa的父节点后返回再走到fa再走到v的期望+
走到fa的非v的子节点再返回fa再走到v的期望。
同样地考虑简化。(自己推)
得到:
这两个式子已经很优秀了。
而且同时解决了上面为什么期望值是整数的问题。
答案是可以的。
我们分析式子f先。
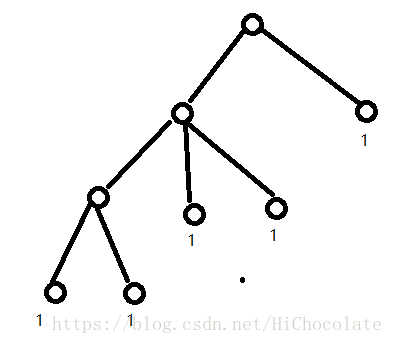
我们画一棵树。
明显,对于叶子节点的f就为1(deg)
那么我们可以看做是叶子节点计算了一次连接它的边:
(为了方便表示,红色边为表示被计算了一次)
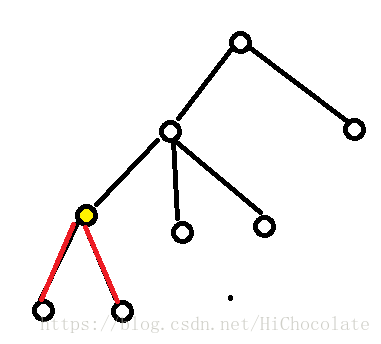
然后我们看看黄色的点。
那么这个黄色的点的f就为5(f[son]=2,deg=5)
然后同样地可以用上面的方法来看:
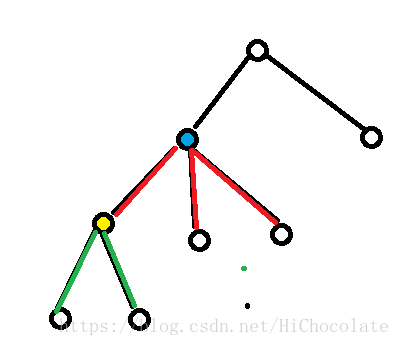
(绿色表示计算了两次)
于是,黄色的点计算完之后图长这样。
然后蓝色的点的f为11(f[son]=7,deg=4)
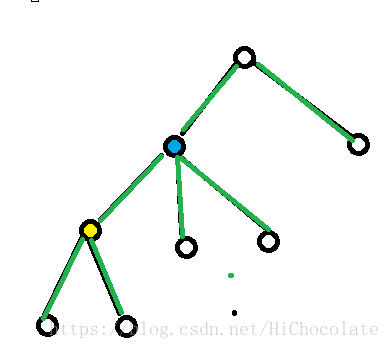
依然覆盖
最后就会变成满屏的绿
于是,我们就可以发现,f[x]的式子即表示为:
siz为当前点为根的子树大小
然后,同样的,g也可以用上面的思想来算。
注意,f是针对子树的,那么g则是针对除了它的子树的计算方法。
那么g[x]的式子即表示为:
这就灰常地优美了。
然后,我们求出一个siz,然后直接跑一遍,求出f与g。
然后,由于我们是求x→lca。lca→y
那么每次就把f[x]、g[x]加上他们的父亲即可。
由于本人比较蒟,只好打一个树链剖分的求lca。然而实验证明,在随机数据的情况下,这种方法比树上rmq更优。
###代码
uses math;
type
new=record
f,g:int64;
end;
var
tot,i,j,k,l,n,m,x,y,ans,answer,gs,a,b,nx,ny,lca:longint;
tov,next,last,size,f,g,father,dep,son,siz,tree,pre,top,fa:array[0..300000] of int64;
ff,gg:array[1..100000,1..3] of int64;
tr:array[1..400000] of new;
procedure insert(x,y:longint);
begin
inc(tot);
tov[tot]:=y;
next[tot]:=last[x];
last[x]:=tot;
end;
procedure dfsf(v,fa:longint);
var
i,j,k,l:longint;
begin
father[v]:=fa;
i:=last[v];
f[v]:=2*siz[v]-1;
g[v]:=2*(n-siz[v])-1;
if v<>1 then
begin
f[v]:=f[v]+f[fa];
g[v]:=g[v]+g[fa];
end;
while i<>0 do
begin
if tov[i]<>fa then
begin
dfsf(tov[i],v);
end;
i:=next[i];
end;
end;
procedure dfsfd(x,f,d:longint);
var
i,j,k,l:longint;
begin
fa[x]:=f;
dep[x]:=d;
siz[x]:=1;
i:=last[x];
while i<>0 do
begin
if tov[i]<>fa[x] then
begin
dfsfd(tov[i],x,d+1);
siz[x]:=siz[x]+siz[tov[i]];
if (son[x]=0) or (siz[tov[i]]>siz[son[x]]) then son[x]:=tov[i];
end;
i:=next[i];
end;
end;
procedure dfs(v,num:longint);
var
i,j,k,l:longint;
begin
inc(gs);
tree[v]:=gs;
top[v]:=num;
pre[gs]:=v;
if son[v]=0 then exit;
dfs(son[v],num);
i:=last[v];
while i<>0 do
begin
if tov[i]<>fa[v] then
begin
if tov[i]<>son[v] then
begin
dfs(tov[i],tov[i]);
end;
end;
i:=next[i];
end;
end;
function getans(x,y:longint):longint;
var
i,j,tx,ty,k:longint;
begin
tx:=top[x];
ty:=top[y];
while tx<>ty do
begin
if dep[tx]<dep[ty] then
begin
y:=fa[ty];
ty:=top[y];
end
else
begin
x:=fa[tx];
tx:=top[x];
end;
end;
if dep[x]>dep[y] then exit(y)
else exit(x);
end;
begin
assign(input,'tree.in');reset(input);
assign(output,'tree.out');rewrite(output);
readln(n,m);
for i:=1 to n-1 do
begin
readln(x,y);
insert(x,y);
insert(y,x);
inc(size[x]);
inc(size[y]);
end;
dfsfd(1,0,1);
dfs(1,1);
f[1]:=-1;
g[1]:=-1;
dfsf(1,0);
for i:=1 to m do
begin
readln(a,b);
lca:=getans(a,b);
writeln((f[a]-f[lca]+g[b]-g[lca]) mod 1000000007);
end;
end.




 浙公网安备 33010602011771号
浙公网安备 33010602011771号