摘要：
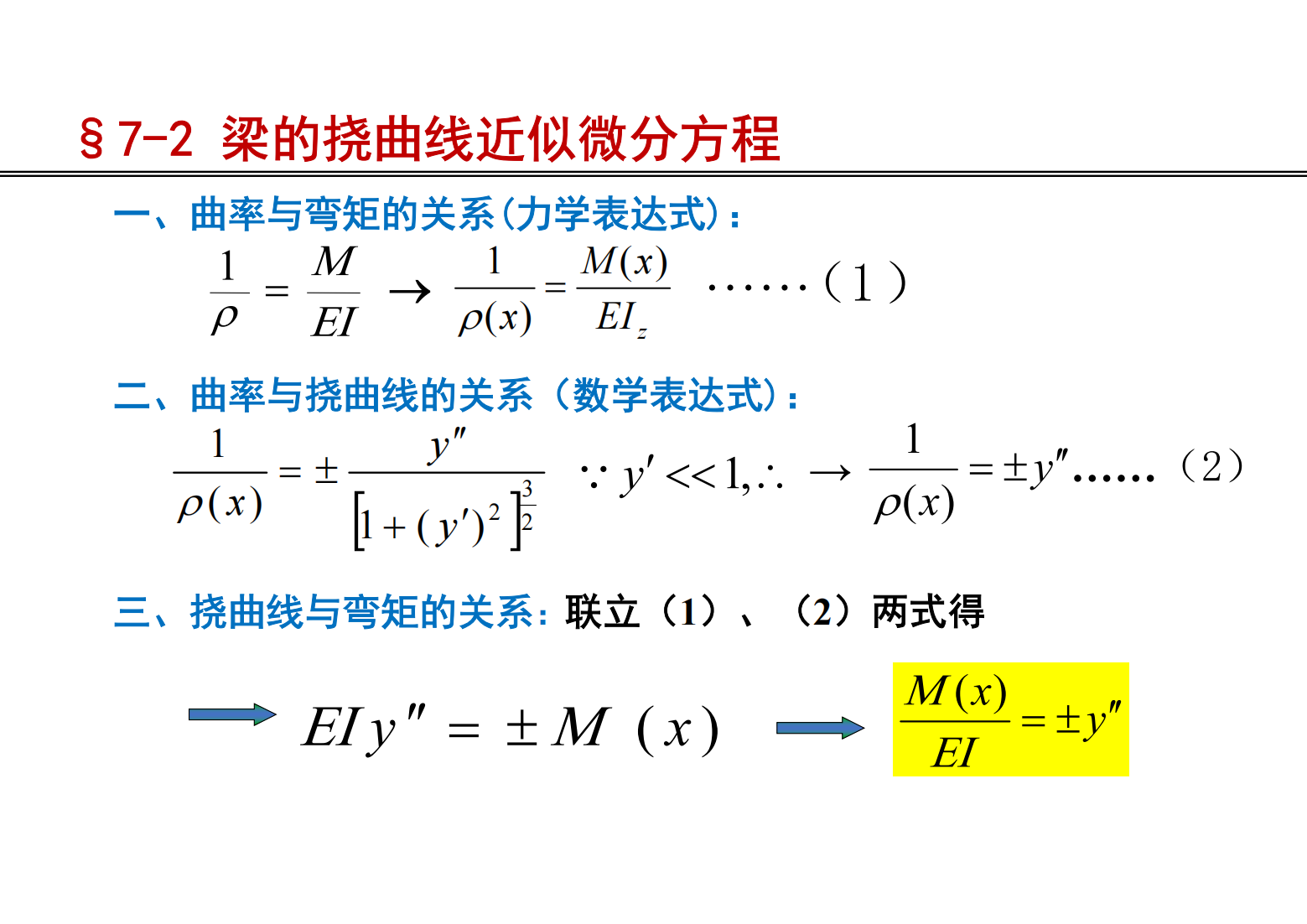
§ 7-2 梁的挠曲线近似微分方程 \[EIy^{\prime\prime}=\pm M(x) \Rightarrow \frac{M(x)}{EI}=\pm y^{\prime\prime} \]§ 7-3 积分法计算梁的变形 \[EIy^{\prime\prime}(x)=-M(x) \]\[E 阅读全文
posted @ 2024-11-18 20:27
RES_HON
阅读(29)
评论(0)
推荐(0)
摘要：
  
评论(0)
推荐(0)
摘要：
5.2 中心极限定理 中心极限定理 定理 5.6（林德伯格-莱维中心极限定理） 设 \(X_1, X_2, \cdots, X_n, \cdots\) 是独立同分布的随机变量序列，且 \(E(X_1) = \mu\), \(D(X_1) = \sigma^2\)。记 \[Y_n = \frac{\s 阅读全文
posted @ 2024-11-18 18:06
RES_HON
阅读(85)
评论(0)
推荐(0)
摘要：
5.2 中心极限定理 定义和基础概念 定义 5.2（按分布收敛） 设随机变量序列 \(X_n\) 和随机变量 \(X\) 的分布函数分别为 \(F_n(x)\) 和 \(F(x)\)。如果对 \(F(x)\) 的任一连续点 \(x\)，都有 \[\lim_{n \to \infty} F_n(x) 阅读全文
posted @ 2024-11-18 18:05
RES_HON
阅读(58)
评论(0)
推荐(0)
摘要：
1.Leibniz积分法则 Leibniz积分法则是一种处理含参数定积分对参数求导的公式，广泛应用于变上限和变参数的积分问题。 一般形式: 对于一个函数 \(f(x,\alpha)\), 定积分定义为: \[I(\alpha) = \int_{a(\alpha)}^{b(\alpha)} f(x,\ 阅读全文
posted @ 2024-11-18 08:45
RES_HON
阅读(170)
评论(0)
推荐(0)
浙公网安备 33010602011771号