各种排序算法详解

1、插入排序

插入排序简单来说就是遍历到 第 i 个元素时，前面 i-1 个元素已经排好了序，因此第 i个元素只需要从第i-1个元素向前比较，找到第一个小于等于它的元素插入在其后面即可，相应的后面的元素向后挪动

 

 

 插入排序的算法复杂度：最坏和平均时间复杂度都为O(n^2)，如果输入数据已经排序好了则为O(n)

2、希尔排序

希尔排序其实还是插入排序，不过他对数组的元素进行排序时需要一个增量，并且按照增量序列进行排序，增量序列一般为（数组大小为n）（n/2，n/4，......，1)，

然后按照增量序列对间隔增量的元素排序，比如当增量为n/2，就对a[x],a[x+n/2]...这些间隔n/2的元素序列进行插入排序

 

 

 希尔排序的最坏时间复杂度为O(n^2)

3、堆排序

首先我们需要了解堆的结构和性质，堆可以用一个一维数组表示，一般使用完全二叉树来表示堆，其实就是将数组中的数按完全二叉树一行一行排列下来

堆分最小堆和最大堆，最小堆的根节点为最小值，然后其子节点都比根节点大（可能会等于）

堆有两个操作，一个是自上而下的操作，一般是在一维数组上面建堆或者删除堆中的元素会用到，另一个是自下而上的操作，一般是在插入元素后用到，元素插入在堆末尾，然后根据堆的性质遍历该元素的父节点。

使用堆排序其实就是先建立一个最大堆，然后交换根节点和堆中最后一个元素的值，然后对此时的根节点进行自伤而下的操作（此时堆的元素数相当于上一次操作时的元素个数-1），然后继续重复这一步操作即可

 

 

 

 

 

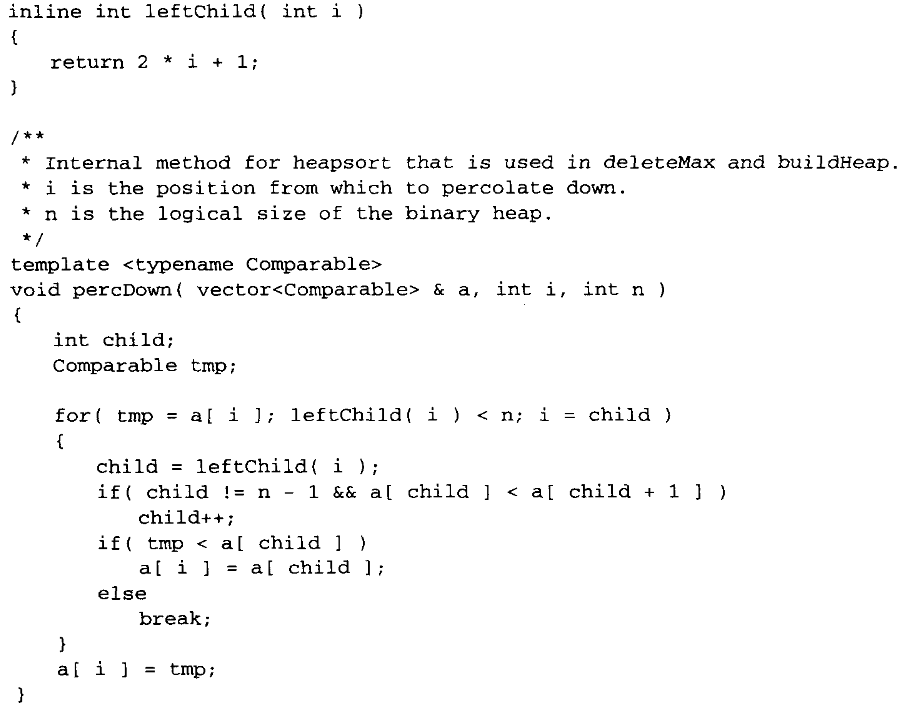
 堆排序的最坏的时间复杂度为O(NlogN)，比较稳定

4、归并排序

归并排序运用分治的思想，不断将原数组分割成两部分，直到某一部分的元素为1，然后进行合并，合并时可以看作两个已经排好序的数组合并成为一个有序数组，只需要线性的时间

 

 

 

 

归并排序的最坏时间复杂度为O(NlogN)

5、快速排序

快速排序分为以下四步

 

 选取枢纽元十分重要，一种比较好的办法是三数中值分割法，如下：

 

 

 

 分割策略也是十分重要的，我们一般采取如果数组左边元素等于枢纽元时，停止，右边等于枢纽元时也停止，然后交换，虽然没什么意义，但是一般采取这样的策略

 

 

 

 

 

快速排序的平均时间复杂度为O(NlogN)，最坏的情况为O(n^2)