B树——思路、及C语言代码的实现
0.序
本人现读本科大二,这学期学习数据结构,老师为我们的期末作业布置一道任选题,而我一直以来都有听说B树是一棵挺神奇的树,所以我选择了它,当然更重要的原因是因为B树的难度最高,我喜欢做有挑战性的工作。同时,我听我基友说他热衷于将自己所学所想分享到博客园上,故才有了这样一篇文章。希望我能够在写博客的同时学习到更多东西,同时也能帮助到其他遇到或者即将遇到雷同问题的初学者们。
1.关于B树
B树是一种称之为查找树的树,与之类似的有查找二叉树,平衡二叉树,除此之外,还有各种B树的兄弟姐妹B+树、B-树、B*树等,他们共同的特点就是都是按照一定的顺序规律存储的。B树的应用也是很广泛的,B树是几乎所有数据库的默认索引结构,也是用的最多的索引结构。B树是一种多叉树,根据其最多叉的数目可以直接称为M阶B树。根据算法导论上叙述,还可按B树每个节点最少的分支确定一棵B树的阶,但是这样的话B树的阶便必须为偶数。我个人是使用根据最大分支的数目确定B树的阶的。
下图就是某一棵B树,每一个结点中都包含有数个数据元素,而同时一定会有数据元素的个数加一个的子树。
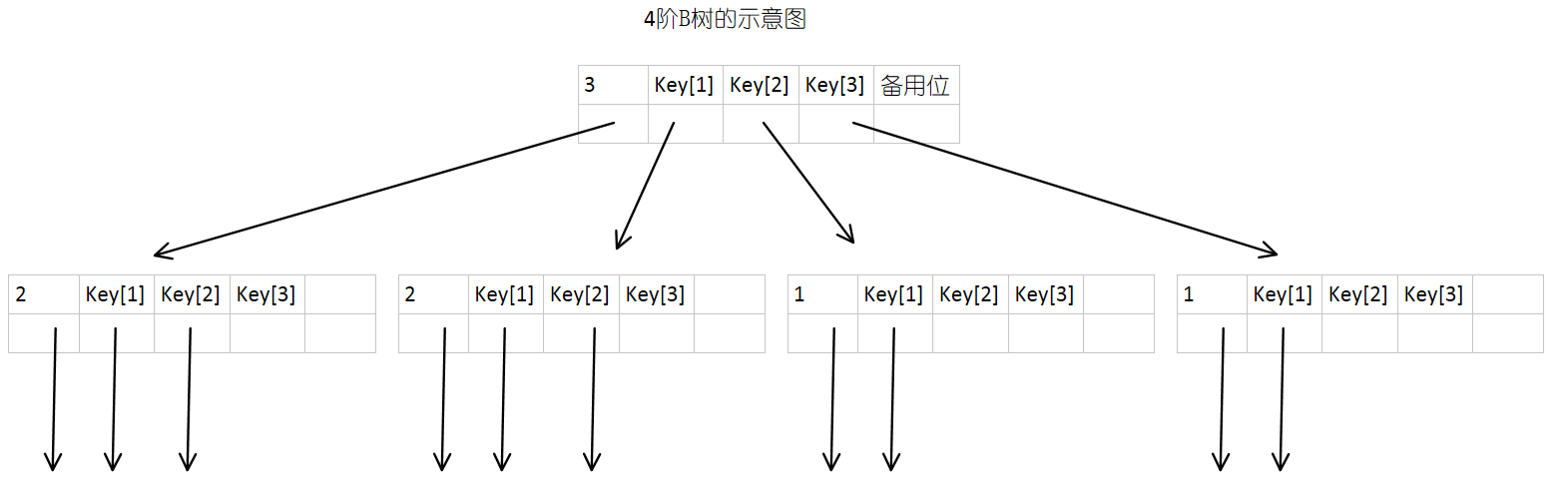
一棵M阶B树或为空树,或为满足下列特性的M叉树:
(1)树中每个结点最多含有M棵子树;
(2)若根结点不是叶子结点,则至少有2棵子树;
(3)除根结点之外的所有非终端结点至少有[m/2]棵子树;
(4)每个非终端结点中包含的信息keynum,ptr[0],key[1],ptr[1],key[2],ptr[2],……key[keynum],ptr[keynum];
其中,key为关键字,且关键字按升序排序,ptr为指向子树的根结点指针
2.思路及实现
B树的接口主要是插入(包括空树插入一个元素)和删除操作,而插入和删除操作不可避免的都会用到查找操作,而查找的主要思路比较简单,主要是利用B树是一种排序树的原理,可以很快找到要插入位置或者要删除结点。这里的关键是注意返回内容包括查找结果所在结点,以及该元素所在位置,这是为了方便接下来的操作比较简单。
插入:
通过对B树进行遍历,找出要插入的结点以及结点位置,如果找到的key值在B树当中已经存在,则说明插入失败,否则,就可以进行插入操作。这里可以先不管是否超出M阶树的上限要求,因为我们在定义的时候会故意留下一个位置,可以存放多余的一个元素,插入之后,通过判断是否达到M阶树上限要求,再进行递归的分裂操作。
1 /*** 2 * @name Status insertBTree(BTree &T, Record e) 3 * @description 插入实现元素的插入 4 * @return 成功返回OK,如果存在则返回FALSE,否则返回ERROR 5 * @notice 6 ***/ 7 Status insertBTree(BTree &T, Record e) 8 { 9 BTree p; 10 int index, temp; 11 Status find_flag; 12 if (NULL == T)//考虑B树为空树的情况 13 { 14 T = (BTree)malloc(BTLEN); 15 if (NULL == T) return OVERFLOW; 16 T->keynum = 1; 17 T->parent = NULL; 18 for (index = 0;index <= m; ++index) 19 { 20 T->ptr[index] = NULL; 21 T->key[index] = 0; 22 } 23 T->key[1] = e.key; 24 return OK; 25 } 26 find_flag = findBTree(T, p, temp, e.key);//寻找插入节点 27 if (find_flag == TRUE) 28 { 29 return FALSE; 30 } 31 if (find_flag == FALSE) 32 { //不管怎样先直接插入 33 p->keynum++; 34 for (index = p->keynum;index > temp;--index) 35 { 36 p->key[index] = p->key[index - 1]; 37 p->ptr[index] = p->ptr[index - 1]; 38 } 39 p->ptr[temp] = NULL; 40 p->key[temp] = e.key; 41 if (p->keynum == m) //这种情况得分裂 42 { 43 splitBTree(p); 44 } 45 renewParent(T); 46 return OK; 47 } 48 return ERROR; 49 }
分裂:
分裂操作是插入操作过程中一个最重要的操作,因为这是处理“冲突”(即结点中的数据元素大于B树规则中要求的最大个数)的一个通用的处理方式,这种方式必须要对所有的情况都适用,而分裂是解决这一问题一个方法。当然这种方法只是考虑到效率,没有对兄弟可否借数据进行判断,但是另外一种方式比较麻烦,这里先不做讨论。
分裂的思路是让父亲结点先腾出一个位置(包括key和ptr)出来,然后在需要分裂的结点里面取中间的元素并且移动中间的元素key到父亲结点已经腾出来的key位置那里,然后把分裂出来的右部分接到腾出来的ptr那里。注意整个过程对左部分和右部分的都要改变元素的个数以及清空一些没用的空间。在往上分裂之后可能会造成一种情况,就是父亲结点也可能达到分裂的最大个数,所以,检查父亲结点是否需要分裂,需要的话,递归之。
1 /*** 2 * @name status splitBTree(BTree T) 3 * @description 递归实现分裂节点操作 4 * @return 成功返回OK,否则返回ERROR 5 * @notice 6 ***/ 7 Status splitBTree(BTree T) //此时分裂的节点一定会是超出最大值的。 8 { 9 BTree t1, t2; 10 int index, index_1; 11 if (T->parent == NULL) 12 { 13 t1 = (BTree)malloc(BTLEN); 14 if (NULL == t1) return OVERFLOW; 15 t2 = (BTree)malloc(BTLEN); 16 if (NULL == t2) return OVERFLOW; 17 18 t1->keynum = m / 2; 19 t2->keynum = m - (m / 2) - 1; 20 t1->parent = T; 21 t2->parent = T; 22 for (index = 0;index <= m; ++index) //先全部初始化 23 { 24 t1->ptr[index] = NULL; 25 t1->key[index] = 0; 26 t2->ptr[index] = NULL; 27 t2->key[index] = 0; 28 } 29 for (index = 0;index <= m / 2; ++index) //初始化t1 30 { 31 t1->ptr[index] = T->ptr[index]; 32 t1->key[index] = T->key[index]; 33 } 34 t2->ptr[0] = T->ptr[(m / 2) + 1]; 35 for (index = (m / 2) + 2;index <= m; ++index) //初始化t2 36 { 37 t2->ptr[index - ((m / 2) + 1)] = T->ptr[index]; 38 t2->key[index - ((m / 2) + 1)] = T->key[index]; 39 } 40 T->keynum = 1; 41 T->ptr[0] = t1; 42 T->ptr[1] = t2; 43 T->key[1] = T->key[m / 2 + 1]; 44 for (index = 2;index <= m; ++index) //初始化T 45 { 46 T->ptr[index] = NULL; 47 T->key[index] = 0; 48 } 49 return OK; 50 }
删除:
B树元素的删除操作与插入操作类似,但是却要麻烦,因为得分两种情况处理。(1)寻找到存在这个元素,而且这个元素所在是叶子节点(即它的孩子为空),直接对其进行删除,之后再判断是否小于B树规则中要求的最小的子树个数。如果小于,那就调用合并函数。(2)如果寻找到的这个元素是非叶子节点的元素,通过寻找比该元素小的最大元素(该元素肯定为叶子节点),把该元素直接赋值给要删除的元素,再在叶子节点处进行(1)中的操作。
1 /*** 2 * @name Status deleteBTreeRecord(BTree &T, Record e) 3 * @description 实现B树元素的删除 4 * @return 成功返回OK,否则返回ERROR 5 * @notice 6 ***/ 7 Status deleteBTreeRecord(BTree &T, Record e) 8 { 9 BTree p, q; 10 int num, temp, index; 11 Status find_flag; 12 if (T == NULL) 13 return ERROR; 14 find_flag = findBTree(T, p, temp, e.key); 15 if (find_flag == FALSE) 16 { 17 return FALSE; 18 } 19 if (find_flag == TRUE) 20 { 21 //deleteBTreeBNode(p,temp); 22 if (p->ptr[temp] == NULL) //如果是叶子节点的话 23 { 24 for (index = temp;index <= p->keynum;++index) 25 { 26 p->key[index] = p->key[index + 1]; 27 p->ptr[index] = p->ptr[index + 1]; 28 } 29 p->keynum--; 30 if (p->keynum == (m + 1) / 2 - 2) 31 { 32 //调用借兄弟的函数 33 if (borrowBNode(p) == EMPTY) T = NULL; 34 else renewParent(T); 35 } 36 return OK; 37 } 38 else //不是叶子结点的话 39 { 40 //遍历 41 findMax(p->ptr[temp - 1], q, num);//返回的q一定会是叶子节点 42 p->key[temp] = q->key[num]; 43 q->key[num] = 0; 44 q->keynum--; 45 if (q->keynum == (m + 1) / 2 - 2) 46 { 47 //调用借兄弟的函数 48 if (borrowBNode(q) == EMPTY) T = NULL; 49 else renewParent(T); 50 } 51 return OK; 52 } 53 return OK; 54 } 55 return ERROR; 56 }
合并:
在此先声明,因为一开始只考虑B树的阶为4的情况,后来改为使用宏定义阶M的数值,所以这段代码存在BUG,只支持阶为3或4的B树= =。
思路还是挺清晰的,首先先向兄弟结点借元素,如果兄弟能够借给你元素的话(即借了你之后并不会小于最少的分支),那么直接从兄弟那里取元素,否则,和兄弟合并。
合并其实是分裂反过来的情况,从父亲结点那里取出一个key值介于要合并的两个结点之间的元素,插入左部分最末尾处,同时右部分插到左部分后面,然后父亲结点元素依次往前挪。从而实现合并操作。之后,也必须对父亲结点进行判断是否小于最小的分支数,如果也小于,对父亲节点进行递归操作。
1 /*** 2 * @name Status borrowBNode(BTree &T) 3 * @description 递归实现,向兄弟借元素,否则和兄弟合并 4 * @return 成功返回OK,否则返回ERROR 5 * @notice 这种情况应该是T为单元素结点 6 ***/ 7 Status borrowBNode(BTree T) 8 { 9 int mynum, bronum, index; 10 BTree b = NULL, f = NULL; 11 if (T == NULL) return ERROR; 12 f = T->parent; 13 if (f == NULL)//考虑父亲结点不存在的情况 14 { 15 if (T->keynum == 0) 16 { 17 f = T->ptr[0]; 18 if (f == NULL) 19 { 20 free(T); 21 return EMPTY; 22 } 23 for (index = 0;index <= f->keynum;index++) 24 { 25 T->key[index] = f->key[index]; 26 T->ptr[index] = f->ptr[index]; 27 } 28 T->keynum = f->keynum; 29 free(f); 30 renewParent(T); 31 } 32 return OK; 33 } 34 mynum = whichSon(T); 35 if (mynum == 0) 36 bronum = 1; 37 else 38 bronum = mynum - 1; 39 b = f->ptr[bronum]; 40 if (b->keynum == (m + 1) / 2 - 1) //如果兄弟帮不了你了 41 { 42 //那么就和这个兄弟合体 43 if (bronum < mynum) //如果我不是第一个 44 { 45 b->keynum++; 46 b->key[b->keynum] = f->key[mynum]; 47 b->ptr[b->keynum] = T->ptr[0]; 48 for (index = 1;index <= T->keynum;index++) 49 { 50 b->key[index + b->keynum] = T->key[index]; 51 b->ptr[index + b->keynum] = T->ptr[index]; 52 b->keynum++; 53 } 54 free(T); 55 for (index = mynum;index <= f->keynum;index++) 56 { 57 f->key[index] = f->key[index + 1]; 58 f->ptr[index] = f->ptr[index + 1]; 59 } 60 f->keynum--; 61 } 62 else 63 { 64 T->keynum++; 65 T->key[T->keynum] = f->key[bronum]; 66 T->ptr[T->keynum] = b->ptr[0]; 67 for (index = 1;index <= b->keynum;index++) 68 { 69 T->key[index + T->keynum] = b->key[index]; 70 T->ptr[index + T->keynum] = b->ptr[index]; 71 T->keynum++; 72 } 73 free(b); 74 for (index = bronum;index <= f->keynum;index++) 75 { 76 f->key[index] = f->key[index + 1]; 77 f->ptr[index] = f->ptr[index + 1]; 78 } 79 f->keynum--; 80 } 81 renewParent(f); 82 if (f->keynum == (m + 1) / 2 - 2) 83 { 84 //调用借兄弟的函数 85 return borrowBNode(f); 86 } 87 } 88 else//如果兄弟能够帮你 89 { 90 if (bronum < mynum) //如果我不是第一个 91 { 92 for (index = 1;index <= T->keynum;index++) 93 { 94 T->key[index + 1] = T->key[index]; 95 T->ptr[index + 1] = T->ptr[index]; 96 } 97 T->ptr[1] = T->ptr[0]; 98 T->key[1] = f->key[mynum]; 99 T->ptr[0] = b->ptr[b->keynum]; 100 T->keynum++; 101 f->key[mynum] = b->key[b->keynum]; 102 b->key[b->keynum] = 0; 103 b->ptr[b->keynum] = NULL; 104 b->keynum--; 105 106 } 107 else //如果我是第一个 108 { 109 T->keynum++; 110 T->key[T->keynum] = f->key[1]; 111 T->ptr[T->keynum] = b->ptr[0]; 112 f->key[1] = b->key[1]; 113 b->ptr[0] = b->ptr[1]; 114 for (index = 1;index <= b->keynum;index++) 115 { 116 b->key[index] = b->key[index + 1]; 117 b->ptr[index] = b->ptr[index + 1]; 118 } 119 b->keynum--; 120 } 121 } 122 return OK; 123 }
遍历,输出:
为了让B树更容易看,代码更容易调试,我同时还用队列写了个层次遍历,这个看看就好,实现起来挺麻烦的。而且可能代码实现也存在问题
1 /*** 2 * @name Status ergodic(BTree T, LinkList L, int newline, int sum) 3 * @description print需要用到的递归遍历程序 4 * @return 成功返回OK 5 * @notice 此处用到队列 6 ***/ 7 Status ergodic(BTree T, LinkList L, int newline, int sum) 8 { 9 int index; 10 BTree p; 11 if (T != NULL) 12 { 13 printf("[ "); 14 Enqueue_L(L, T->ptr[0]); 15 for (index = 1;index <= T->keynum; index++) 16 { 17 printf("%d ", T->key[index]); 18 Enqueue_L(L, T->ptr[index]); 19 } 20 sum += T->keynum + 1; 21 printf("]"); 22 if (newline == 0) 23 { 24 printf("\n"); 25 newline = sum - 1; 26 sum = 0; 27 } 28 else 29 { 30 --newline; 31 } 32 } 33 if (IfEmpty(L) == FALSE) 34 { 35 Dequeue_L(L, p); 36 ergodic(p, L, newline, sum); 37 } 38 return OK; 39 } 40 /*** 41 * @name Status print(BTree T) 42 * @description 层次遍历并分层输出B树 43 * @return 成功返回OK 44 * @notice 45 ***/ 46 Status print(BTree T) 47 { 48 LinkList L; 49 if (T == NULL) 50 { 51 printf("[ ]\n"); 52 return OK; 53 } 54 InitQueue_L(L); 55 ergodic(T, L, 0, 0); 56 DestroyQueue(L); 57 return OK; 58 }
3.测试
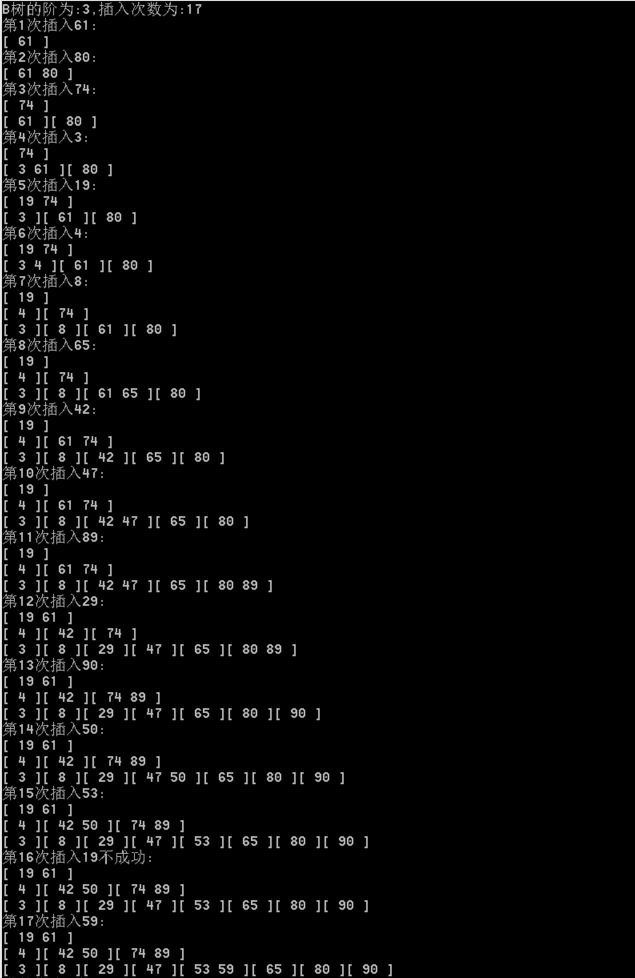
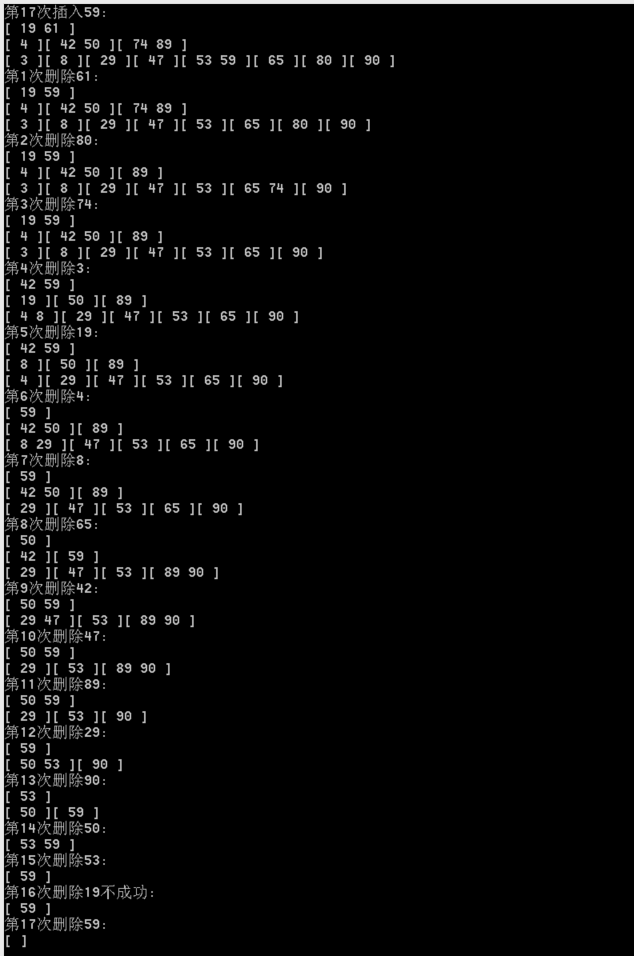
4.总结
以目前所掌握的知识,终于把B树做出来了,整个过程没有参考过其他人的代码,所以并不知道自己的一些思路是否得当,如有错误,多多包涵。在整个过程中,最难,卡的最久的也就是合并操作了,这块的代码也是乱得掉渣,以后有时间把他完善了。最后附上完整代码。

1 #define _CRT_SECURE_NO_WARNINGS 2 #include<stdio.h> 3 #include<stdlib.h> 4 #include<time.h> 5 #define BTREELENGTH 50 6 #define BTLEN (sizeof(BTNode)) 7 #define MAXINT 100 8 typedef enum status 9 { 10 TRUE, 11 FALSE, 12 OK, 13 ERROR, 14 OVERFLOW, 15 EMPTY 16 }Status; 17 typedef int KeyType; 18 19 //**********************************B树**************************************** 20 #define m 3 // B树的阶,此设为4 21 typedef struct 22 { 23 KeyType key; 24 char data; 25 } Record; 26 typedef struct BTNode 27 { 28 int keynum; // 结点中关键字个数,即结点的大小 29 struct BTNode *parent; // 指向双亲结点 30 KeyType key[m + 1]; // 关键字向量,0号单元未用 31 struct BTNode *ptr[m + 1]; // 子树指针向量 32 // Record *recptr[m + 1]; // 记录指针向量,0号单元未用 33 //在此添加其他自定义数据 34 } BTNode, *BTree; // B树结点和B树的类型 35 typedef struct 36 { 37 BTNode *pt; // 指向找到的结点 38 int i; // 1..m,在结点中的关键字序号 39 int tag; // 1:查找成功,0:查找失败 40 } Result; // 在B树的查找结果类型 41 //**********************************B树**************************************** 42 43 //**********************************队列*************************************** 44 typedef struct LNode { 45 BTree data; // 数据域 46 struct LNode *next; // 指针域 47 } LNode, *LinkList; 48 //**********************************队列*************************************** 49 50 /*** 51 * @name Status InitQueue_L(LinkList &L) 52 * @description 初始化队列 53 * @return 成功返回OK,开辟空间失败返回OVERFLOW 54 * @notice 55 ***/ 56 Status InitQueue_L(LinkList &L) 57 { // 初始化一个只含头结点的空单链表L 58 if (NULL == (L = (LNode*)malloc(sizeof(LNode)))) // 生成新结点 59 return OVERFLOW; 60 L->next = NULL; 61 return OK; 62 } 63 /*** 64 * @name LNode* MakeNode_L(BTree e) 65 * @description 构造队列结点 66 * @return 返回结点地址 67 * @notice 68 ***/ 69 LNode* MakeNode_L(BTree e) 70 { // 构造数据域为e的单链表结点 71 LNode *p; 72 p = (LNode*)malloc(sizeof(LNode)); // 分配结点空间 73 if (p != NULL) 74 { 75 p->data = e; 76 p->next = NULL; 77 } 78 return p; 79 } 80 /*** 81 * @name Status Enqueue_L(LNode *p, BTree e) 82 * @description 队列的入队 83 * @return 成功返回OK,否则返回ERROR 84 * @notice 85 ***/ 86 Status Enqueue_L(LNode *p, BTree e) 87 { //在p结点之后插入q结点 88 if (NULL == p) return ERROR; // 参数不合理 89 while (p->next != NULL) 90 p = p->next; 91 p->next = MakeNode_L(e); // 对应图4.11(b)的②,修改p结点的指针域 92 return OK; 93 } 94 95 /*** 96 * @name Status Dequeue_L(LNode *p, BTree &e) 97 * @description 队列的出队 98 * @return 成功返回OK,否则返回ERROR 99 * @notice 100 ***/ 101 Status Dequeue_L(LNode *p, BTree &e) 102 { 103 // 删除p结点的直接后继结点并用参数e返回被删结点的值 104 LNode *q; 105 if (NULL == p || NULL == p->next) return ERROR; // 删除位置不合理 106 q = p->next; 107 p->next = q->next; // 修改被删结点q的指针域 108 e = q->data; 109 free(q); // 释放结点q 110 return OK; 111 } 112 113 /*** 114 * @name void DestroyQueue(LinkList L) 115 * @description 队列的销毁 116 * @return 无返回 117 * @notice 118 ***/ 119 void DestroyQueue(LinkList L) 120 { 121 // 销毁整个链表 122 LinkList p; 123 if (L != NULL) 124 { 125 p = L; 126 L = L->next; 127 free(p); 128 DestroyQueue(L); 129 } 130 } 131 /*** 132 * @name Status IfEmpty(LinkList L) 133 * @description 判断队列是否为空 134 * @return 空返回TRUE,不空返回FALSE,否则返回ERROR 135 * @notice 136 ***/ 137 Status IfEmpty(LinkList L) 138 { 139 if (L == NULL) return ERROR; 140 if (L->next == NULL) return TRUE; 141 return FALSE; 142 } 143 /*** 144 * @name Status ergodic(BTree T, LinkList L, int newline, int sum) 145 * @description print需要用到的递归遍历程序 146 * @return 成功返回OK 147 * @notice 此处用到队列 148 ***/ 149 Status ergodic(BTree T, LinkList L, int newline, int sum) 150 { 151 int index; 152 BTree p; 153 if (T != NULL) 154 { 155 printf("[ "); 156 Enqueue_L(L, T->ptr[0]); 157 for (index = 1;index <= T->keynum; index++) 158 { 159 printf("%d ", T->key[index]); 160 Enqueue_L(L, T->ptr[index]); 161 } 162 sum += T->keynum + 1; 163 printf("]"); 164 if (newline == 0) 165 { 166 printf("\n"); 167 newline = sum - 1; 168 sum = 0; 169 } 170 else 171 { 172 --newline; 173 } 174 } 175 if (IfEmpty(L) == FALSE) 176 { 177 Dequeue_L(L, p); 178 ergodic(p, L, newline, sum); 179 } 180 return OK; 181 } 182 /*** 183 * @name Status print(BTree T) 184 * @description 层次遍历并分层输出B树 185 * @return 成功返回OK 186 * @notice 187 ***/ 188 Status print(BTree T) 189 { 190 LinkList L; 191 if (T == NULL) 192 { 193 printf("[ ]\n"); 194 return OK; 195 } 196 InitQueue_L(L); 197 ergodic(T, L, 0, 0); 198 DestroyQueue(L); 199 return OK; 200 } 201 202 /*** 203 * @name Status findMax(BTree T, BTree &p,int ans) 204 * @description 寻找最大关键字的结点,T为要寻找的树,p为返回的节点,ans为第几个 205 * @return 成功返回OK,否则返回ERROR 206 * @notice 207 ***/ 208 Status findMax(BTree T, BTree &p, int &ans) 209 { 210 if (T == NULL) 211 return ERROR; 212 p = T; 213 while (p->ptr[p->keynum] != NULL) 214 { 215 p = p->ptr[p->keynum]; 216 } 217 ans = p->keynum; 218 return OK; 219 } 220 /*** 221 * @name Status findMin(BTree T, BTree &p,int ans) 222 * @description 寻找最小关键字的结点,T为要寻找的树,p为返回的节点,ans为第几个 223 * @return 成功返回OK,否则返回ERROR 224 * @notice 225 ***/ 226 /*** 227 * @name Status findBTree(BTree T, BTree &p, int &ans, KeyType k) 228 * @description 寻找 ,T为要寻找的树,p为返回的节点,ans为第几个元素,k为要找的值 229 * @return 成功返回OK,否则返回ERROR 230 * @notice 231 ***/ 232 Status findBTree(BTree T, BTree &p, int &ans, KeyType k) 233 { 234 BTree q; 235 int index = 1; 236 KeyType keynow; 237 if (T == NULL) 238 return ERROR; 239 q = T; 240 keynow = T->key[1]; 241 while (q != NULL) //深度的遍历 242 { 243 index = 1; 244 keynow = q->key[index]; 245 while (index <= q->keynum) //节点内对各真值进行遍历 246 { 247 if (k == keynow) //找到元素 248 { 249 p = q; 250 ans = index; 251 return TRUE; 252 } 253 if (k > keynow) 254 { 255 if (index == q->keynum) 256 { 257 if (q->ptr[index] == NULL) 258 { 259 p = q; 260 ans = q->keynum + 1; 261 return FALSE; 262 } 263 q = q->ptr[index]; 264 break; 265 } 266 ++index; 267 keynow = q->key[index]; 268 continue; 269 } 270 if (k < keynow) 271 { 272 if (q->ptr[index - 1] == NULL) 273 { 274 p = q; 275 ans = index; 276 return FALSE; 277 } 278 q = q->ptr[index - 1]; 279 break; 280 } 281 } 282 } 283 284 return ERROR; 285 } 286 /*** 287 * @name Status renewParent(BTree p) 288 * @description 告诉孩子们亲身爸爸是谁 289 * @return 成功返回OK,否则返回ERROR 290 * @notice 291 ***/ 292 Status renewParent(BTree p) 293 { 294 int index; 295 if (p == NULL) return ERROR; 296 for (index = 0;index <= p->keynum;++index) 297 { 298 if (p->ptr[index] != NULL) 299 { 300 p->ptr[index]->parent = p; 301 renewParent(p->ptr[index]); 302 } 303 } 304 return OK; 305 } 306 /*** 307 * @name int whichSon(BTree T) 308 * @description 找出是父亲的第几个孩子 309 * @return 成功返回第几个孩子,否则返回-1 310 * @notice 311 ***/ 312 int whichSon(BTree T) 313 { 314 int index = -1; 315 if (T == NULL) return -1; 316 for (index = 0;index <= T->parent->keynum;++index) //找出是父亲的第几个孩子 317 { 318 if (T->parent->ptr[index] == T) return index; 319 } 320 return -1; 321 } 322 /*** 323 * @name status splitBTree(BTree T) 324 * @description 递归实现分裂节点操作 325 * @return 成功返回OK,否则返回ERROR 326 * @notice 327 ***/ 328 Status splitBTree(BTree T) //此时分裂的节点一定会是超出最大值的。 329 { 330 BTree t1, t2; 331 int index, index_1; 332 if (T->parent == NULL) 333 { 334 t1 = (BTree)malloc(BTLEN); 335 if (NULL == t1) return OVERFLOW; 336 t2 = (BTree)malloc(BTLEN); 337 if (NULL == t2) return OVERFLOW; 338 339 t1->keynum = m / 2; 340 t2->keynum = m - (m / 2) - 1; 341 t1->parent = T; 342 t2->parent = T; 343 for (index = 0;index <= m; ++index) //先全部初始化 344 { 345 t1->ptr[index] = NULL; 346 t1->key[index] = 0; 347 t2->ptr[index] = NULL; 348 t2->key[index] = 0; 349 } 350 for (index = 0;index <= m / 2; ++index) //初始化t1 351 { 352 t1->ptr[index] = T->ptr[index]; 353 t1->key[index] = T->key[index]; 354 } 355 t2->ptr[0] = T->ptr[(m / 2) + 1]; 356 for (index = (m / 2) + 2;index <= m; ++index) //初始化t2 357 { 358 t2->ptr[index - ((m / 2) + 1)] = T->ptr[index]; 359 t2->key[index - ((m / 2) + 1)] = T->key[index]; 360 } 361 T->keynum = 1; 362 T->ptr[0] = t1; 363 T->ptr[1] = t2; 364 T->key[1] = T->key[m / 2 + 1]; 365 for (index = 2;index <= m; ++index) //初始化T 366 { 367 T->ptr[index] = NULL; 368 T->key[index] = 0; 369 } 370 return OK; 371 } 372 373 index = whichSon(T); 374 for (index_1 = T->parent->keynum;index_1 > index;--index_1) //腾出父亲的位置 375 { 376 T->parent->ptr[index_1 + 1] = T->parent->ptr[index_1]; 377 T->parent->key[index_1 + 1] = T->parent->key[index_1]; 378 } 379 T->parent->keynum++; 380 T->parent->key[index + 1] = T->key[m / 2 + 1]; 381 t2 = T->parent->ptr[index + 1] = (BTree)malloc(BTLEN); 382 if (NULL == t2) return OVERFLOW; 383 for (index = 0;index <= m; ++index) //先全部初始化 384 { 385 t2->ptr[index] = NULL; 386 t2->key[index] = 0; 387 } 388 t2->keynum = m - (m / 2) - 1; 389 t2->parent = T->parent; 390 t2->ptr[0] = T->ptr[(m / 2) + 1]; 391 for (index = (m / 2) + 2;index <= m; ++index) //初始化t2 392 { 393 t2->ptr[index - ((m / 2) + 1)] = T->ptr[index]; 394 t2->key[index - ((m / 2) + 1)] = T->key[index]; 395 } 396 T->keynum = m / 2; 397 for (index = (m / 2) + 1;index <= m; ++index) //初始化t2 398 { 399 T->ptr[index] = NULL; 400 T->key[index] = 0; 401 } 402 if (T->parent->keynum == m) 403 { 404 splitBTree(T->parent); 405 } 406 return OK; 407 } 408 /*** 409 * @name Status insertBTree(BTree &T, Record e) 410 * @description 插入实现元素的插入 411 * @return 成功返回OK,如果存在则返回FALSE,否则返回ERROR 412 * @notice 413 ***/ 414 Status insertBTree(BTree &T, Record e) 415 { 416 BTree p; 417 int index, temp; 418 Status find_flag; 419 if (NULL == T) 420 { 421 T = (BTree)malloc(BTLEN); 422 if (NULL == T) return OVERFLOW; 423 T->keynum = 1; 424 T->parent = NULL; 425 for (index = 0;index <= m; ++index) 426 { 427 T->ptr[index] = NULL; 428 T->key[index] = 0; 429 } 430 T->key[1] = e.key; 431 return OK; 432 } 433 find_flag = findBTree(T, p, temp, e.key); 434 if (find_flag == TRUE) 435 { 436 return FALSE; 437 } 438 if (find_flag == FALSE) 439 { //不管怎样先直接插入 440 p->keynum++; 441 for (index = p->keynum;index > temp;--index) 442 { 443 p->key[index] = p->key[index - 1]; 444 p->ptr[index] = p->ptr[index - 1]; 445 } 446 p->ptr[temp] = NULL; 447 p->key[temp] = e.key; 448 if (p->keynum == m) //这种情况得分裂 449 { 450 splitBTree(p); 451 } 452 renewParent(T); 453 return OK; 454 } 455 return ERROR; 456 } 457 /*** 458 * @name Status borrowBNode(BTree &T) 459 * @description 递归实现,向兄弟借元素,否则和兄弟合并 460 * @return 成功返回OK,否则返回ERROR 461 * @notice 这种情况应该是T为单元素结点 462 ***/ 463 Status borrowBNode(BTree T) 464 { 465 int mynum, bronum, index; 466 BTree b = NULL, f = NULL; 467 if (T == NULL) return ERROR; 468 f = T->parent; 469 if (f == NULL)//考虑父亲结点不存在的情况 470 { 471 if (T->keynum == 0) 472 { 473 f = T->ptr[0]; 474 if (f == NULL) 475 { 476 free(T); 477 return EMPTY; 478 } 479 for (index = 0;index <= f->keynum;index++) 480 { 481 T->key[index] = f->key[index]; 482 T->ptr[index] = f->ptr[index]; 483 } 484 T->keynum = f->keynum; 485 free(f); 486 renewParent(T); 487 } 488 return OK; 489 } 490 mynum = whichSon(T); 491 if (mynum == 0) 492 bronum = 1; 493 else 494 bronum = mynum - 1; 495 b = f->ptr[bronum]; 496 if (b->keynum == (m + 1) / 2 - 1) //如果兄弟帮不了你了 497 { 498 //那么就和这个兄弟合体 499 if (bronum < mynum) //如果我不是第一个 500 { 501 b->keynum++; 502 b->key[b->keynum] = f->key[mynum]; 503 b->ptr[b->keynum] = T->ptr[0]; 504 for (index = 1;index <= T->keynum;index++) 505 { 506 b->key[index + b->keynum] = T->key[index]; 507 b->ptr[index + b->keynum] = T->ptr[index]; 508 b->keynum++; 509 } 510 free(T); 511 for (index = mynum;index <= f->keynum;index++) 512 { 513 f->key[index] = f->key[index + 1]; 514 f->ptr[index] = f->ptr[index + 1]; 515 } 516 f->keynum--; 517 } 518 else 519 { 520 T->keynum++; 521 T->key[T->keynum] = f->key[bronum]; 522 T->ptr[T->keynum] = b->ptr[0]; 523 for (index = 1;index <= b->keynum;index++) 524 { 525 T->key[index + T->keynum] = b->key[index]; 526 T->ptr[index + T->keynum] = b->ptr[index]; 527 T->keynum++; 528 } 529 free(b); 530 for (index = bronum;index <= f->keynum;index++) 531 { 532 f->key[index] = f->key[index + 1]; 533 f->ptr[index] = f->ptr[index + 1]; 534 } 535 f->keynum--; 536 } 537 renewParent(f); 538 if (f->keynum == (m + 1) / 2 - 2) 539 { 540 //调用借兄弟的函数 541 return borrowBNode(f); 542 } 543 } 544 else//如果兄弟能够帮你 545 { 546 if (bronum < mynum) //如果我不是第一个 547 { 548 for (index = 1;index <= T->keynum;index++) 549 { 550 T->key[index + 1] = T->key[index]; 551 T->ptr[index + 1] = T->ptr[index]; 552 } 553 T->ptr[1] = T->ptr[0]; 554 T->key[1] = f->key[mynum]; 555 T->ptr[0] = b->ptr[b->keynum]; 556 T->keynum++; 557 f->key[mynum] = b->key[b->keynum]; 558 b->key[b->keynum] = 0; 559 b->ptr[b->keynum] = NULL; 560 b->keynum--; 561 562 } 563 else //如果我是第一个 564 { 565 T->keynum++; 566 T->key[T->keynum] = f->key[1]; 567 T->ptr[T->keynum] = b->ptr[0]; 568 f->key[1] = b->key[1]; 569 b->ptr[0] = b->ptr[1]; 570 for (index = 1;index <= b->keynum;index++) 571 { 572 b->key[index] = b->key[index + 1]; 573 b->ptr[index] = b->ptr[index + 1]; 574 } 575 b->keynum--; 576 } 577 } 578 return OK; 579 } 580 581 /*** 582 * @name Status deleteBTreeRecord(BTree &T, Record e) 583 * @description 实现B树元素的删除 584 * @return 成功返回OK,否则返回ERROR 585 * @notice 586 ***/ 587 Status deleteBTreeRecord(BTree &T, Record e) 588 { 589 BTree p, q; 590 int num, temp, index; 591 Status find_flag; 592 if (T == NULL) 593 return ERROR; 594 find_flag = findBTree(T, p, temp, e.key); 595 if (find_flag == FALSE) 596 { 597 return FALSE; 598 } 599 if (find_flag == TRUE) 600 { 601 //deleteBTreeBNode(p,temp); 602 if (p->ptr[temp] == NULL) //如果是叶子节点的话 603 { 604 for (index = temp;index <= p->keynum;++index) 605 { 606 p->key[index] = p->key[index + 1]; 607 p->ptr[index] = p->ptr[index + 1]; 608 } 609 p->keynum--; 610 if (p->keynum == (m + 1) / 2 - 2) 611 { 612 //调用借兄弟的函数 613 if (borrowBNode(p) == EMPTY) T = NULL; 614 else renewParent(T); 615 } 616 return OK; 617 } 618 else //不是叶子结点的话 619 { 620 //遍历 621 findMax(p->ptr[temp - 1], q, num);//返回的q一定会是叶子节点 622 p->key[temp] = q->key[num]; 623 q->key[num] = 0; 624 q->keynum--; 625 if (q->keynum == (m + 1) / 2 - 2) 626 { 627 //调用借兄弟的函数 628 if (borrowBNode(q) == EMPTY) T = NULL; 629 else renewParent(T); 630 } 631 return OK; 632 } 633 return OK; 634 } 635 return ERROR; 636 } 637 /*** 638 * @name Status initBTree(BTree &t) 639 * @description 初始化一个空B树 640 * @return 成功返回OK 641 * @notice 642 ***/ 643 Status initBTree(BTree &t) 644 { 645 t = NULL; 646 return OK; 647 } 648 /*** 649 * @name Status test() 650 * @description 针对数据结构实验做的测试函数 651 * @return 成功返回OK 652 * @notice 653 ***/ 654 Status test() 655 { 656 // 测试代码 657 int n, i; 658 int arr[BTREELENGTH]; 659 BTree a; 660 Record d; 661 srand((unsigned)time(NULL)); 662 n = rand() % BTREELENGTH; 663 //scanf("%d", &n); //可以改为自己输入数据 664 printf("B树的阶为:%d,插入次数为:%d\n", m, n); 665 initBTree(a); 666 for (i = 0;i < n;i++) 667 { 668 d.key = rand() % MAXINT; 669 //scanf("%d", &d.key); //可以改为自己输入数据 670 arr[i] = d.key; 671 if (insertBTree(a, d) == OK) 672 printf("第%d次插入%d:\n", i + 1, d.key); 673 else 674 printf("第%d次插入%d不成功:\n", i + 1, d.key); 675 print(a); 676 } 677 for (i = 0;i < n;i++) 678 { 679 d.key = arr[i]; 680 if (deleteBTreeRecord(a, d) == OK) 681 printf("第%d次删除%d:\n", i + 1, d.key); 682 else 683 printf("第%d次删除%d不成功:\n", i + 1, d.key); 684 print(a); 685 } 686 return OK; 687 688 } 689 /*** 690 主函数 691 ***/ 692 int main() 693 { 694 test(); 695 return 0; 696 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号