题解：T3 世界 / CF1184D2

T3 世界 / CF1184D2

其实挺有趣的对吧，不过就是少取模导致怒调 3h，你能理解我把

f[i][j] += mod,f[i][j] %= mod;

加上后答案突然变了的绝望感吗？？？？？？？？？

首先考虑最基本的 60 分做法。

首先说赛时思路（和题解状态不太一样，不过这个做法无法优化。。。）设 \(f_{l,r}\) 为当前所在的这个点左边有 \(l\) 个点，右边有 \(r\) 个点时的期望剩余数量。

大概就是 \(1 \cdots l,k,k+1\cdots r\)。

因为发现是求期望，直接大胆设状态的值时当前状态到达目标状态的期望。

那么显然有：

\[f_{0,i}=f_{i,0}=i \]

接下来考虑怎么转移：

首先设当前点为 \(k\)，左边有 \(l\)，右边有 \(r\)。

有 \(1-\frac{l+r+1}{m}\) 的概率加入一个点。

有 \(\frac{l+1}{r+l+2}\) 的概率在 \(k\) 的左边加入一个点，贡献为 \(f_{l+1,r}\)。

有 \(\frac{r+1}{r+l+2}\) 的概率在 \(k\) 的右边加入一个点，贡献为 \(f_{l,r+1}\)。

有 \(\frac{l+r+1}{m}\) 的概率删除一个点。

在 \(k\) 的左边删除一个点，考虑枚举到底删到那个点，假设删了前 \(j\) 个点，概率均为 \(\frac{1}{l+r}\) 贡献为 \(f_{l-j,r}\)，即 \(\frac{1}{l+r}\sum_{j=1}^{l}{f_{l-j,r}}\)。

在 \(k\) 的右边删除一个点，考虑枚举到底删到那个点，假设删了后 \(j\) 个点，概率均为 \(\frac{1}{l+r}\) 贡献为 \(f_{l,r-j}\)，即 \(\frac{1}{l+r}\sum_{j=1}^{r}{f_{l,r-j}}\)。

容易发现这是有后效性的，并且后效性并不是单层的（类似于树上随机游走）。

所以朴素做法就是直接高消，复杂度 \(O(m^6)\)。

现在考虑怎么优化。

其实这个式子还是可以接着用，不过为方便以及正确性，更改一下状态。

设 \(f_{i,k}\) 表示当前有 \(i\) 个世界，处于第 \(k\) 个世界的期望值。

容易发现其实就是把 \(l\) 变为 \(k - 1\)，\(r\) 变为 \(n - k\)。

建议自己推一下，就是更改一下下标，不然及其容易假......

\[f_{i,1}=f_{i,i}=i \]

\[f_{i,k}=\frac{m-i}{m}\frac{k}{i+1}f_{i+1,k+1}+\frac{m-i}{m}\frac{i-k+1}{i+1}f_{i+1,k}+\frac{i}{m}\frac{1}{i-1}(\sum_{j=k}^{i-1}f_{j,k}+\sum_{j=1}^{k-1}f_{i-k+j,j}) \]

写出这个式子之后观察一下（其实上面的也有这样的性质）就会发现只有一项是 \(k+1\) 其余均为 \(k\)。

所以把 \(f_{i+1,k+1}\) 提到前面，变换一下得：

\[f_{i+1,k+1}=\frac{m(i+1)}{(m-i)k}f_{i,k}-\frac{i-k+1}{k}f_{i+1}{k}-\frac{i(i+1)}{(i-1)(m-i)(k)}(\sum_{j=k}^{i-1}f_{j,k}+\sum_{j=1}^{k-1}f_{i-k+j,j}) \]

惊奇地发现，后效性竟然莫名其妙消失了？吗？

如果直接使用这个式子就会发现端倪，因为如果直接代入样例 \(3,2,3\) 的 \(f_{3,2}\)，就会发现 \(2=\frac{14}{9}\)。

这是为什么呢？

考虑这个式子的本质，其实就是需要由 \(f_{i,k}\) 转移出去而从而反推出 \(f_{i+1,k+1}\)，就像是 \(2=x+1\) 可以推导出 \(x=1\) 一样。

但是有一个问题，那就是在边界处 \(f_{i,1}\) 这个式子是不适用的，而任何推出 \(f_{i+1,2}\) 的式子却都是基于 \(f_{i,1}\) 的式子是对的基础之上的，所以就爆炸了。

那既然无法推出 \(f_{i,1}\) 的形式，那就停在 \(f_{i,2}\) 就好了。

具体就是假设每个 \(f_{i,k}\) 均可表示为 \(\sum_{j=1}^{m}{c_j f_{j,2}+C}\) 的形式，这样就避免了出现错误方程的情况，因为 \(f_{i,2}\) 我们球不出来，就只好设成未知数了。

每次转移的时候处理每一项系数即可，上个前缀和优化即可。

已经表示完了，那怎么求值？

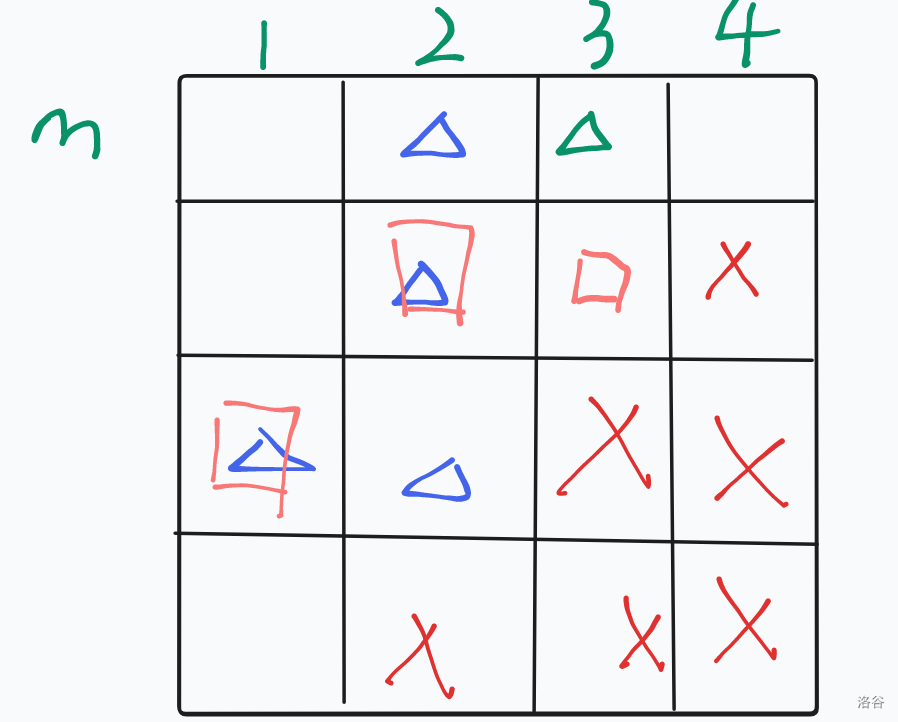
绿色的三角表示当前的 \(f_{m,k}\)，而通过前面的推导已经知道了它关于这些未知数的表达式了，但是有趣的来了，这个点还可以使用粉色正方形来转移，发现这两者的转移并不完全一致，所以可以借此列出方程从而解得所有未知数，然后使用 \(f_{n,k}\) 的转移系数算出即可。

复杂度 \(O(m^3)\)，高斯消元不用优化复杂度 \(O(m^3\log mod)\)。