线段树优化建图

线段树优化建图

远古存货，格式有问题。

适用范围

当边多到根本建不出图时，就需要线段树来助阵了。

实现方法

我们看一道例题。

一个星球上有 \(n\) 个国家和许多双向道路，国家用 \(1\sim n\) 编号。

但是道路实在太多了，不能用通常的方法表示。于是我们以如下方式表示道路：\((a,b),(c,d)\) 表>示，对于任意两个国家 \(x,y\)，如果 \(a\le x\le b,c\le y\le d\)，那么在 \(x,y\) 之间有一条道>路。

首都位于 \(P\) 号国家。你想知道 \(P\) 号国家到任意一个国家最少需要经过几条道路。保证 \(P\) 号国家能到任意一个国家。

发现暴力连边是\(O(n^2)\)的太劣了，而题目给的是区间连向区间，理所当然的想到了最擅长区间操作的分块线段树。

可以把\(m\)条中连入的边用入树维护，连出的边用出树维护。

现在来想两个重要结论。

\([l, r] \in [L, R]\)

1. 如果区间\([l, r]\)有一条连出的边，则\([L, R]\)也一定有。
2. 如果点\(x\)可以到达区间\([L, R]\)，则也一定可以到达\([l, r]\)。

在线段树上便翻译为

1. 出树上一个节点(区间)可由其儿子到达，儿子有，父亲也得有
2. 入树上一个节点(区间)可由其父亲到达，父亲能到，儿子也能到

现在我们可以构建一个虚点，这样便可以降低复杂度，由出树的点指向虚点，再有虚点指向入树的点。

现在为止，我们还差一种边，我们现在从出树出发到达入树后就走不了了TmT，而我们所有的连边都是从出树指向入树，所以我们要讲入树和出树的每一个对应区间节点都连边(入树指向出树)，这样我们就可以愉快地回来啦。

示意图如下：

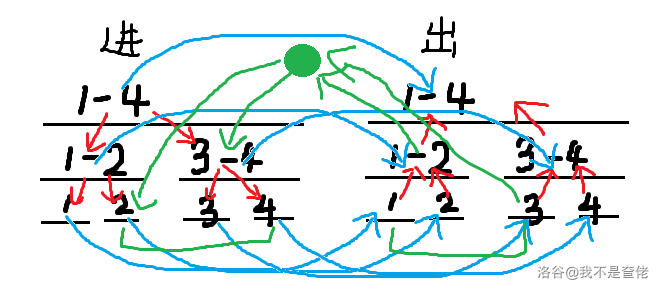
例题

luogu P6348

就是刚刚的例题

code :

#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <bitset>

using namespace std;

const int N = 5e5 + 100, mod = 1e9 + 7;

#define fi first
#define se second
#define lid id * 2
#define rid id * 2 + 1
#define emp emplace_back
#define IL inline
#define reg register
using pii = pair <int, int>;
using llt = long long int;
// #define int long long
int n, m, P;

vector <pii> G[N << 4];

IL void add(int x, int y, int w) {G[x].emp(y, w);}

int dis[N << 4], num[N];

void Build1(int id, int l, int r) // in
{
    add(id, id + n * 4, 0);
    if (l == r) return;
    add(id, lid, 0); add(id, rid, 0);
    int mid = (l + r) >> 1;
    Build1(lid, l, mid); Build1(rid, mid + 1, r);
}

void Build2(int id, int l, int r) // out
{
    if (l == r) return (num[l] = 4 * n + id), void();
    add(lid + 4 * n, id + 4 * n, 0); add(rid + 4 * n, id + 4 * n, 0);
    int mid = (l + r) >> 1;
    Build2(lid, l, mid); Build2(rid, mid + 1, r);
}

void Merge1(int id, int cl, int cr, int l, int r, int p)
{
    if (l <= cl && cr <= r) return add(4 * n + id, p, 1), add(p + 1, id, 1);
    int mid = (cl + cr) >> 1;
    if (l <= mid) Merge1(lid, cl, mid, l, r, p);
    if (r > mid) Merge1(rid, mid + 1, cr, l, r, p);
}

void Merge2(int id, int cl, int cr, int l, int r, int p)
{
    if (l <= cl && cr <= r) return add(id + n * 4, p + 1, 1), add(p, id, 1);
    int mid = (cl + cr) >> 1;
    if (l <= mid) Merge2(lid, cl, mid, l, r, p);
    if (r > mid) Merge2(rid, mid + 1, cr, l, r, p);
}

bitset <N << 4> vis;

void dij(int s)
{
    priority_queue <pii> q;
    memset(dis, 0x3f, sizeof(dis));
    dis[s] = 0;
    q.push({dis[s], s});
    while (q.size())
    {
        int x = q.top().se; q.pop();
        vis[x] = 1;
        for (auto &j : G[x])
        {
            int to = j.fi, w = j.se;
            if (dis[to] > dis[x] + w)
            {
                dis[to] = dis[x] + w;
                if (!vis[to]) q.push({-dis[to], to});
            }
        }
    }
}

signed main()
{
    // freopen("data.in", "r", stdin); freopen("data.out", "w", stdout);
    ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);

    cin >> n >> m >> P; Build1(1, 1, n); Build2(1, 1, n);
    for (int i = 1; i <= m; i++)
    {
        int a, b, c, d; cin >> a >> b >> c >> d;
        Merge1(1, 1, n, a, b, 8 * n + 2 * i);
        Merge2(1, 1, n, c, d, 8 * n + 2 * i);
    }
    dij(num[P]);
    cerr << 1 << ' ';
    for (int i = 1; i <= n; i++)
    {
        cout << dis[num[i]] / 2 << '\n';
    }
}