kruskal 重构树
kruskal 重构树
远古存货,格式有问题。
kruskal 重构树是基于最小生成树的算法,主要用于处理两点之间所有路径中经过的最大边权最小值一类的问题
先将所有边排序,就像kruskal一样,然后每次建一个虚点,由当前边的端点指向这个虚点,这个点的点权便是这条边的边权
就像这样:
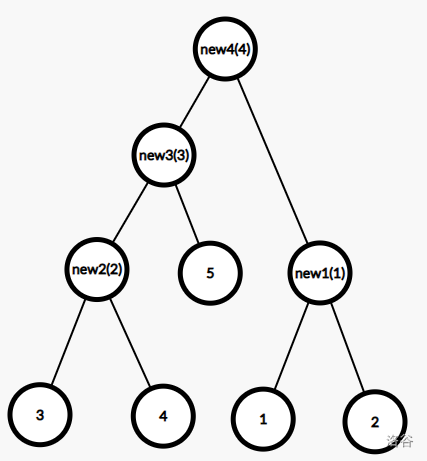
性质:
- 这是一个大根堆
- 两点间的最大边权最小值 = 最小生成树两点间简单路径最大值 = 重构树上两点的 lca
- 二叉树
关于 2 的证明:
既然最大枚举到这条边就联通,所以两点间的最大边权最小值 = 最小生成树两点间简单路径最大值
而重构树讲边权转为点权就与最小生成树完全等价,故而最小生成树两点间简单路径最大值 = 重构树上两点的 lca
code :
void Kruskal()
{
sort(e + 1, e + 1 + m);
for (int i = 1; i <= m; i++)
{
int u = Find(e[i].from), v = Find(e[i].to);
if (u != v)
{
++tot;
fa[u] = fa[v] = tot;
add_new(tot, u); add_new(u, tot);
add_new(tot, v); add_new(v, tot);
val[tot] = e[i].w;
if (tot == 2 * n - 1) break;
}
}
}
例题:
CF 1706
一开始想用可持久化并查集chao过去
但发现查询需要判断区间根是否相同,而可持久化并查集只能维护直接的fa,而不能维护root
所以考虑只查询两个点,那问题不就变成了将编号作为权值,两点之间边最大权值的最小值了吗,不就是kruskal重构树板子吗!
那现在来做区间查询,我们可以将区间\([l, r]\)都联通拆成\((l, l + 1),(l + 1, l + 2)... (r - 1, r)\)全部联通
所以可以将每个相邻点答案存入数据结构,然后每次查询都区间查询max,可以用st表做到\(O(q)\)
code:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 2e5 + 100;
// #define int long long
#define emp emplace_back
#define fi first
#define se second
#define IL inline
using pii = pair <int, int>;
struct Node
{
int nxt, from, to, w;
bool operator < (Node x)
{
return w < x.w;
}
}e[N << 1];
int head[N], cnt;
int fa[N];
int Find(int x)
{
if (fa[x] != x) fa[x] = Find(fa[x]);
return fa[x];
}
IL void add(int x, int y, int w)
{
e[++cnt] = {head[x], x, y, w};
head[x] = cnt;
}
int n, m, tot, val[N];
vector <int> G[N];
IL void add_new(int x, int y) {G[x].emp(y);}
void Kruskal()
{
sort(e + 1, e + 1 + m);
for (int i = 1; i <= m; i++)
{
int u = Find(e[i].from), v = Find(e[i].to);
if (u != v)
{
++tot;
fa[u] = fa[v] = tot;
add_new(tot, u); add_new(u, tot);
add_new(tot, v); add_new(v, tot);
val[tot] = e[i].w;
if (tot == 2 * n - 1) break;
}
}
}
class Sem_Tree
{
public :
#define lid id << 1
#define rid id << 1 | 1
int maxn[N << 2];
void PushUp(int id)
{
maxn[id] = max(maxn[lid], maxn[rid]);
}
void Build(int id, int l, int r)
{
maxn[id] = 0;
if (l == r) return (maxn[id] = 0), void();
int mid = (l + r) >> 1;
Build(lid, l, mid); Build(rid, mid + 1, r);
}
void Update(int id, int l, int r, int pos, int val)
{
if (l == r) return (maxn[id] = val), void();
int mid = (l + r) >> 1;
if (pos <= mid) Update(lid, l, mid, pos, val);
else Update(rid, mid + 1, r, pos, val);
PushUp(id);
}
int Query(int id, int cl, int cr, int l, int r)
{
if (l > r) return 0;
if (l <= cl && cr <= r) return maxn[id];
int mid = (cl + cr) >> 1, ans = 0;
if (l <= mid) ans = Query(lid, cl, mid, l, r);
if (r > mid) ans = max(ans, Query(rid, mid + 1, cr, l, r));
return ans;
}
}T;
int dep[N], top[N], siz[N], son[N], f[N], dfn[N], timer;
void dfs(int x, int fa)
{
dep[x] = dep[fa] + 1, siz[x] = 1, f[x] = fa;
int maxson = 0;
for (auto &to : G[x])
{
if (to == fa) continue;
dfs(to, x);
if (siz[to] > maxson) son[x] = to, maxson = siz[to];
siz[x] += siz[to];
}
}
void dfs2(int x, int fa)
{
top[x] = fa, dfn[x] = ++timer;
if (son[x]) dfs2(son[x], fa);
for (auto &to : G[x])
{
if (to == f[x] || to == son[x]) continue;
dfs2(to, to);
}
}
int lca(int x, int y)
{
// cerr << top[y] << ' ';
while (top[x] != top[y])
{
if (dep[top[x]] < dep[top[y]]) swap(x, y);
x = f[top[x]];
}
if (dep[x] > dep[y]) swap(x, y);
return x;
}
int main()
{
// freopen("data.in", "r", stdin); freopen("data.out", "w", stdout);
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
int QQQ; cin >> QQQ;
while (QQQ--)
{
cnt = 0;
cin >> n >> m; tot = n;
int Q; cin >> Q;
for (int i = 1; i <= m; i++)
{
int x, y; cin >> x >> y; add(x, y, i);
}
for (int i = 1; i <= 2 * n; i++) fa[i] = i;
Kruskal();
dfs(tot, 0); dfs2(tot, tot);
T.Build(1, 1, n);
for (int i = 1; i <= n - 1; i++)
{
T.Update(1, 1, n - 1, i, val[lca(i, i + 1)]);
}
while (Q--)
{
int l, r; cin >> l >> r;
cout << T.Query(1, 1, n - 1, l, r - 1) << ' ';
}
cout << '\n';
for (int i = 1; i <= tot; i++) G[i].clear(), val[i] = son[i] = f[i] = siz[i] = dep[i] = top[i] = dfn[i] = 0;
}
}
luogu P4768
没错,我第一思路还是可持久化并查集,好像也确实可以做,就是并查集维护这一颗树内dis的最小值,但我不太想写,所以就用了kruskal重构树练练手
我们先翻译题目,其实就是给定一个图,然后有一些边是可以驱车过去的,而车只要遇到水就会立马报爆炸,我们可以坐车前往所有只经过未被积水侵蚀的边所能到达的点(长难句qwq)
而我们到达驱车到达一个点后,答案不就是这个点到1号点的最短路吗,最后给每个点去个min就过了~
but 枚举点复杂度 \(O(n)\)
所以考虑怎么优化一下,我们发现两个之间点可以驱车到达当且仅当两点之间存在一条路径使得其最小边权大于水位线,这不就是 kruskal 重构树最擅长的吗?
所以我们理所当然的建出了重构树
由于所有实点都是叶子节点所以不用考虑子树内的情况
我们发现两个非常有用的性质
-
从一个点向上走点权一定单调不增
-
在一个点的子树内的任意两点的lca都在其子树内,即任意两点lca的点权都大于这个点的点权
由这两个性质可以很容易发现,答案其实就是深度最小的大于水位线的点所对应的其子树内dis的最小值。
于是一个二分+预处理每个点最小的dis即可轻松通过。
细节:
二分的时候可以二分深度,然后用倍增向上跳来找到这个点
code :
// 1. dij
// 2. kruskal
// 3. brainy sreach
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <queue>
#include <bitset>
using namespace std;
const int N = 4e5 + 100;
#define fi first
#define se second
#define lid id << 1
#define rid id << 1 | 1
#define emp emplace_back
#define IL inline
#define reg register
using pii = pair <int, int>;
using llt = long long int;
int dis[N], w[N], n, m, fa[N << 1], f[N << 1][32], dep[N << 1], cnt, tot, head[N], val[N], ans[N];
bitset <N> vis;
vector <pii> G[N];
vector <int> E[N];
struct Star
{
int nxt, from, to, w;
bool operator < (Star y)
{
return w > y.w;
}
}e[N << 1];
IL void add(int x, int y, int w)
{
e[++cnt] = {head[x], x, y, w};
head[x] = cnt;
}
void dij()
{
priority_queue <pii> q;
memset(dis, 0x3f, sizeof(dis));
vis.reset();
q.push({0, 1});
dis[1] = 0;
while (q.size())
{
int x = q.top().se; q.pop();
vis[x] = 1;
for (auto &j : G[x])
{
int to = j.fi, w = j.se;
if (dis[to] > dis[x] + w)
{
dis[to] = dis[x] + w;
if (vis[to]) continue;
q.push({-dis[to], to});
}
}
}
}
IL int Find(int x)
{
if (x != fa[x]) fa[x] = Find(fa[x]);
return fa[x];
}
IL void add_e(int x, int y)
{
E[x].emp(y);
}
void Kruskal()
{
sort(e + 1, e + 1 + cnt);
for (int i = 1; i <= cnt; i++)
{
int u = Find(e[i].from), v = Find(e[i].to);
if (Find(u) == Find(v)) continue;
++tot;
fa[u] = tot, fa[v] = tot, val[tot] = e[i].w;
add_e(u, tot), add_e(tot, u);
add_e(v, tot), add_e(tot, v);
if (tot == 2 * n - 1) break;
}
}
void dfs(int x, int fa)
{
dep[x] = dep[fa] + 1, f[x][0] = fa, ans[x] = dis[x];
for (reg int i = 1; i <= 20; i++)
{
f[x][i] = f[f[x][i - 1]][i - 1];
}
for (auto & to : E[x])
{
if (to == fa) continue;
dfs(to, x);
ans[x] = min(ans[x], ans[to]);
}
}
IL int Query(int x, int depth)
{
for (reg int i = 18; ~i; --i)
{
if (depth & (1 << i)) x = f[x][i];
}
return x;
}
IL int calc(int x, int w)
{
int l = 1, r = dep[x], mid, pos = 1;
while (l <= r)
{
mid = (l + r) >> 1;
if (val[Query(x, dep[x] - mid)] > w) r = mid - 1, pos = mid;
else l = mid + 1;
}
// cerr << pos << ' ';
return ans[Query(x, dep[x] - pos)];
}
int main()
{
// freopen("data.in", "r", stdin); freopen("data.out", "w", stdout);
ios :: sync_with_stdio(false), cin.tie(0), cout.tie(0);
int T; cin >> T;
while (T--)
{
cin >> n >> m;
tot = n;
for (int i = 1; i <= (n << 1); i++) fa[i] = i;
for (int i = 1, x, y, w, h; i <= m; i++)
{
cin >> x >> y >> w >> h;
add(x, y, h);
G[x].emp(y, w); G[y].emp(x, w);
}
memset(val, 0x3f, sizeof(val));
dij(); Kruskal(); dfs(tot, 0);
int Q, K, S, lastans = 0; cin >> Q >> K >> S;
while (Q--)
{
int pos, w; cin >> pos >> w;
if (K == 1) pos = (pos + K * lastans - 1) % n + 1, w = (w + K * lastans) % (S + 1);
// cerr << pos << ' ' << w << '\n';
cout << (lastans = calc(pos, w)) << '\n';
}
for (int i = 1; i <= (n << 1); i++)
{
dep[i] = ans[i] = 0;
G[i].clear(); E[i].clear();
cnt = 0;
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号