ACM notes
写在前面
提醒
复杂度带 \(log\) 考虑 二分
看到 \(mex\),中位数考虑 二分
看到分数式子求和考虑 整除分块
区间不单调且单峰考虑 三分
看到位运算考虑 拆位
求方案数 考虑 组合数,卡特兰数
构造 考虑 贪心,取余(如四色问题(mod 4), 二分图(mod 2))
DP 考虑 DS
对一个区间内部改变 考虑 该区间的值只由区间端点决定 (如 01 串中 \(n_{10}\) - \(n_{01}\))
考虑 裴蜀定理
考虑 倍增,倍减,分治
考虑 图论
init
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
const double pi = acos(-1);
const double E = exp(1);
constexpr ll mod = 1e9 + 7;
// constexpr int inf = 0x3f3f3f3f;
constexpr ll inf = 0x3f3f3f3f3f3f3f3f;
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int tt = 1;
cin >> tt;
while (tt--) {
}
}
对拍
run.bat
@echo off
set p=a
set l=1
set r=3
cd %p%
g++ -std=c++2a %p%.cpp -o a.out
for /l %%i in (%l%, 1, %r%) do (
a.out < %%i.in > %%i.out
fc /A %%i.out %%i.ans
if errorlevel 1 (
echo TC %%i Failed ======================================== %%i
) else (
echo TC %%i Passed
)
)
cd ..
beat.bat
@echo off
set p=a
set t=10
set len=100
set l=100
set /a r=%l%+%len%
cd %p%
g++ -std=c++2a %p%.cpp -o a.out
g++ -std=c++2a gen.cpp -o gen.out
g++ -std=c++2a ok.cpp -o ok.out
for /l %%i in (%l%, 1, %r%) do (
gen.out > %%i.in
a.out < %%i.in > %%i.out
ok.out < %%i.in > %%i.ans
fc /A %%i.out %%i.ans
if errorlevel 1 (
echo TC %%i Failed ======================================== %%i
@REM 把错误数据放到既定顺序的测试点
copy %%i.in %t%.in
copy %%i.out %t%.out
copy %%i.ans %t%.ans
cd ..
GOTO :RM
) else (
echo TC %%i Passed
)
)
@REM 删除对拍生成的临时文件
:RM
for /l %%i in (%l%, 1, %r%) do (
del %%i.in
del %%i.out
del %%i.ans
)
cd ..
目录结构
Competition
a
*.in
*.out
*.ans
a.cpp
gen.cpp
ok.cpprun.bat
beat.bat
实操视频
check
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
void Data()
{
ofstream fout(".\\Competition\\00check\\1input.txt");
random_device rd;
uniform_int_distribution<ll> dist(1, 100000000);
cout << 1 << "\n";
int n = 7, q = dist(rd) % 4 + 1;
cout << n << "\n";
for (int i = 1; i <= n; ++ i) {
int ai = dist(rd) % n + 1;
cout << ai << " \n"[i == n];
}
vector<int> p(n + 1);
iota(p.begin() + 1, p.end(), 0);
random_shuffle(p.begin() + 1, p.end());
for (int i = 1; i <= n; ++ i) {
// int ai = rng() % n;
cout << p[i] << " \n"[i == n];
}
fout.close();
}
int main() {
srand((unsigned)time(nullptr));
for (int i = 0; i < 10000; ++i) {
printf("Case: %d\n", i);
Data();
system(".\\Competition\\00check\\AC.exe < .\\Competition\\00check\\1input.txt > .\\Competition\\00check\\ACout.txt");
system(".\\Competition\\00check\\WA.exe < .\\Competition\\00check\\1input.txt > .\\Competition\\00check\\WAout.txt");
// getchar(); // 单步回车
// system("fc WAout.txt ACout.txt");
if (system("fc .\\Competition\\00check\\WAout.txt .\\Competition\\00check\\ACout.txt")) { // 自动比较
puts("WA!!!");
break;
}
}
return 0;
}
gen
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
const double pi = acos(-1);
const double E = exp(1);
constexpr ll mod = 1e9 + 7;
// constexpr int inf = 0x3f3f3f3f;
constexpr ll inf = 0x3f3f3f3f3f3f3f3f;
std::mt19937 rng(std::chrono::steady_clock::now().time_since_epoch().count());
int du(ll l, ll r) {
ll len = r - l;
return l + rng() % (len + 1ll);
}
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
int N1 = 100;
int N2 = 25;
int N3 = 50;
int n = du(2, N1);
int m = du(0, N2);
int k = du(1, N3);
cout << n << " ";
cout << m << " ";
cout << k << "\n";
}
交互
int tt = 1;
cin >> tt;
while (tt--) {
int n, x;
cin >> n;
vector<vector<int>> adj(n + 1, vector<int>(0));
vector<int> intr(n + 1), sta(n + 1);
iota(sta.begin(), sta.end(), 0);
int top = n;
auto query = [&](int u, int v) {
cout << "? " << u << " " << v << endl;
cin >> x;
return x;
};
int maxq = 15 * n;
int cnt = 0;
intr[1] = 1;
while (top > 0) {
int m = sta[top]; top --;
if (intr[m] == 1) continue;
int l = 1, r = m;
while (1) {
int cur = query(l, r);
cnt++;
assert(cnt > maxq);
if (cur == l) {
intr[r] = 1;
add(l, r);
break;
}
if (intr[cur] == 1) {
l = cur;
} else {
r = cur;
}
}
top++;
sta[top] = m;
}
}
语言基础
输入输出
getline()输入
cin 和 getline()同时用时需要ignore
string s1,s2;
cin >> s1;
cin.ignore();
getline(cin, s2);
cout << s1 << " " << s2 << "\n";
格式输出
double ans = 0;
cout << fixed << setprecision(9) << ans << "\n"; //保留9位
cout << setfill(' ') << setw(10) << ans << "\n"; //前面填充
for(int i = 0; i < 10; ++i) { //行末无空格
cout << i << " \n"[i == 9];
}
全排列
sort(p.begin(), p.end());
do {
} while (next_permutation(p.begin(), p.end()));
STL容器
将il数组赋初值从 base 开始每位等于前一位加一
iota(il.begin(), il.end(), base);
vector 向量数组
定义 vector
vector<int> ver1(n); // 开了一个容量为n的vector数组
vector<vector<int>> ver3(n); // 二维向量数组,开了n个vector数组
vector<vector<vector<int>>> ver4(n); // 三维向量数组
定义时赋值
vector<int> ver6(n, 1); // 将vector内的初值全部置为1
vector<vector<char>> ver7(n, vector<char>(m, 'a')); // 将二维数组内的值全部置为'a'
对vector进行操作
以下定义时必须保证数据类型相同
// 定义了一个长度为4, 类型为int,内容为{23, 3, 4, 56}数组
vector ver8 = {23, 3, 4, 56};
// 定义了一个长度为3, 类型为pair,内容为{pair{1, 3}, pair{2, 4}, pair{2, 3}}数组
vector ver9 = {pair{1, 3}, pair{2, 4}, pair{2, 3}};
vector ver10 = {vector{1, 2}, vector{23, 43}};
// 在ver8数组中插入n个vector{-1, -2, -3}的数组
vector<vector<int>> ver11(n, vector{-1, -2, -3});
在数组末尾插入一个数
v.push_back(20), v2.push_back({1, 1});
v.emplace_back(21), v2.emplace_back(2, 2); // 与上一个操作相同但速度更快
v.pop_back(); // 删除v数组中的最后一个元素, 时间复杂度O(1)
v.erase(v.begin()); // 删除v数组中的第一个元素,时间复杂O(n)
cout << "返回数组长度:" << v.size() << ' ' << size(v) << '\n';
cout << "返回数组第一个元素" << v[0] << ' ' << v.begin()[0] << "\n";
cout << "返回数组最后一个元素" << v.back() << ' ' << v.rbegin()[0] << "\n";
v.assign(3, 2); // 更改v数组的容量大小和初值,时间复杂度为O(n), 谨慎使用
vector<int> sv;
v.swap(sv); // 交换sv和v中的内容,时间复杂度为O(1)
v = sv; // 赋值操作,将v变为sv
v.insert(v.end(), v.begin(), v.end()); // 在v的末尾插入v数组, 时间复制O(n)
v.insert(v.begin() + 1, sv.end(), sv.end()); // 在v下班为1的位置开始插入sv数组
v.erase(v.begin() + 1, v.end()); // 将v数组从下标1开始全部删除,常用在去重
v.clear(); // 将v数组清空
函数操作
int k = 1;
vector a = {1, 3, 3, 8, 5, 6, 7, 7};
random_shuffle(a.begin(), a.end()); // 将数组随机打乱
sort(a.begin(), a.end()); // 对a数组从小到大进行排序
sort(a.rbegin(), a.rend()); // 对a数组从大到小进行排序
stable_sort(a.begin(), a.end()); // 稳定排序,复杂度O(nlogn);
a.erase(unique(a.begin(), a.end()), a.end()); // 对a数组进行去重,首先保证a数组有序
nth_element(a.begin(), a.begin() + k, a.end()); // 数组可以不有序, 查找数组中第k小的元素
iota(a.begin(), a.end(), 1); // 将a数组从1开始赋值
next_permutation(a.begin(), a.end()); // 将当前序列更换为全排列中的下一个序列
reverse(a.begin(), a.end()); // 将a数组倒置
vector 二分
二分查找,返回数组中第一个大于等于k的位置
int pos1 = lower_bound(a.begin(), a.end(), k) - a.begin();
二分查找,返回数组中第一个大于k的位置
int pos2 = upper_bound(a.begin(), a.end(), k) - a.begin();
二分查找,返回数组中第一个小于k的位置
int pos3 = (--lower_bound(a.begin(), a.end(), k)) - a.begin();
二分查找,返回数组中第一个小于等于k的位置
int pos4 = (--upper_bound(a.begin(), a.end(), k)) - a.begin();
返回a数组所有值的合, 其中0为初值,可以自行更改
int sum = accumulate(a.begin(), a.end(), 0LL);
string
定义string类型, 下标从0开始
int n = 10, start = 1, len = 2;
string str; // 定义一个空字符串
string str1 = "abcd"; // 定义一个字符串"abcd"
string str2(10, '1'); // 定义一个长度为n且每个字符都为’1‘的字符串
string str3(str2, start); // 定义一个字符串为str2[start: ], 即str3是从str2的下标start开始的字符拷贝
string str4(str2, start, len); // 定义一个字符串为str2[start: start + len], 即str4是从str2的下标start开始的len个字符的拷贝
对string进行操作
s[x] = 'b'; // 将x位置的值修改为'b'
s += 'c'; // 在s末尾插入一个字符'c'
s = 'a' + s; // 在s开头插入一个'a'
cout << "返回字符串长度: " << s.size() << ' ' << size(s) << '\n';
cout << "返回字符串第一个元素: " << s[0] << ' ' << s.begin()[0] << "\n";
cout << "返回字符串最后一个元素: " << s.back() << ' ' << s.rbegin()[0] << "\n";
cout << "获取字符串从x位置开始的p个字符: " << s.substr(x, p) << "\n";
cout << "获取字符串从x位置开始的所有字符: " << s.substr(x) << "\n";
// 字符串拼接,时间复杂度O(n), 将t插入到s的x位置:
cout << s.substr(0, x) + t + s.substr(x) << '\n';
// 字符串拼接,时间复杂度O(n), 字符串\"1111\"s的x位置:
cout << s.substr(0, x) + string(4, '1') + s.substr(x) << '\n';
s.erase(x); //从字符串s的第x + 1位开始删去所有字符
s.insert(x, t); //从字符串s的第x + 1位处插入字符串t
s.insert(x, p, u); // 从字符串的第x + 1位处连续插入p次字符u
s.replace(0, x, t); //将字符串s的0~x-1位替换成字符串t
s.replace(s.begin(), s.begin() + x, t); //将字符串s的0~x-1位替换成字符串t
// 在字符串s中查找字符串t, 如果找到返回首字母下标,否则返回string::npos, 即-1
int pos = s.find(t);
int rpos = s.rfind(t); // 与find相同,只不过查找的是t最后一次出现的位置
int poss = s.find(t, pos); // 在 s 中自 pos 位置起字符串 t 第一次出现的位置
s = t; // 使s = t
s.swap(t); // 交换s和t的内容
// cout << "判断t串是否为s串的前缀" << s.starts_with(t) << "\n";
// cout << "判断t串是否为s串的后缀" << s.ends_with(t) << "\n";
与字符操作有关的函数
transform(s.begin(), s.end(), s.begin(), ::tolower); // 将字符串全部转为小写
transform(s.begin(), s.end(), s.begin(), ::toupper); // 将字符串全部转为大写
char c = 'a';
cout << "检查字符c是否是字母和数字: " << isalnum(c) << "\n";
cout << "检查字符c是否是字母: " << isalpha(c) << "\n";
cout << "检查字符c是否是数字: " << isdigit(c) << "\n";
cout << "检查字符c是否是小写字母: " << islower(c) << "\n";
cout << "检查字符c是否是大写字母: " << isupper(c) << "\n";
cout << "检查字符c是否是标点符号: " << ispunct(c) << "\n";
int w = 1233;
string sw = "1233", s16 = "FAB", sx = "12A";
cout << "将数字转换为字符串" << to_string(w) << '\n';
cout << "将字符串转化为int类型" << stoi(sw) << '\n';
cout << "将字符串转化为long long类型" << stoll(sw) << '\n';
cout << "将字符串转化为double类型" << stod(sw) << '\n';
cout << "将十六进制字符串转化为long long类型" << stoll(s16, nullptr, 16) << '\n';
x = 12;
cout << "将x进制字符串转化为long long类型" << stoll(sx, nullptr, x) << '\n';
以下操作和用法同vector一样,不再过多赘述,可以将string看成vector
// 将数组随机打乱
random_shuffle(a.begin(), a.end());
// 对a数组从小到大进行排序
sort(a.begin(), a.end());
// 对a数组从大到小进行排序
sort(a.rbegin(), a.rend());
// 稳定排序,复杂度O(nlogn);
stable_sort(a.begin(), a.end());
// 对a数组进行去重,首先保证a数组有序
a.erase(unique(a.begin(), a.end()), a.end());
// 数组可以不有序, 查找数组中第k大的元素
nth_element(a.begin(), a.begin() + k, a.end());
// 将a数组从1开始赋值
iota(a.begin(), a.end(), 1);
// 将当前序列更换为全排列中的下一个序列
next_permutation(a.begin(), a.end());
// 将a数组倒置
reverse(a.begin(), a.end());
// 二分查找,返回数组中第一个大于等于k的位置
int pos1 = lower_bound(a.begin(), a.end(), k) - a.begin();
// 二分查找,返回数组中第一个大于k的位置
int pos2 = upper_bound(a.begin(), a.end(), k) - a.begin();
// 二分查找,返回数组中第一个小于k的位置
int pos3 = (--lower_bound(a.begin(), a.end(), k)) - a.begin();
// 二分查找,返回数组中第一个小于于等于k的位置
int pos4 = (--upper_bound(a.begin(), a.end(), k)) - a.begin();
// 顺序查找,返回第一个为k的值的位置
int pos5 = find(a.begin(), a.end(), k) - a.begin();
// 返回a数组中最大值的位置
int maxa = max_element(a.begin(), a.end()) - a.begin();
// 返回a数组中最小值的位置
int mina = min_element(a.begin(), a.end()) - a.begin();
// 返回数组中的最大值和最小值
cout << ranges::max(a) << " " << ranges::min(a) << '\n';
// 返回a数组所有值的合, 其中0为初值,可以自行更改
int sum = accumulate(a.begin(), a.end(), 0LL);
map
定义,与set一样,内部升序,键值唯一
constexpr int N = 11;
map<int, int> mp1; // 变量映射变量
map<int, vector<int>> mp2; // 变量映射STL容器,不可以是数组
map<map<int, int>, int> mp3; // STL容器映射变量
map<set<int>, vector<int>> mp4; // STL容器映射STL容器
map<string, int, greater<>> mp5; // 定义一个内部降序的映射
vector<map<int, pair<int, int>>> mp6(N); // 定义N个map
map<pair<int, int>, int> mp7[N]; // 定义N个map, 全局
map<int, string> mp8{{1, "a"}, {2, "b"}}; // 定义时初始化
修改, O(logn),操作与set类似,获取到的键值为pair类型
map<int, string> mp;
mp[0] = "STL", mp[1] = "ABC"; // 添加
mp[0] = "pp"; // 修改
mp.erase(mp.begin()); // 删除第一个元素
mp.erase(1); // 删除键为1的元素
mp.clear(); // 清楚map中的元素
for (int i = 3; i <= N; ++i) { mp[i] = to_string(i * i); }
map<int, string> cmp = mp; // 使cmp等于mp
swap(cmp, mp); // 交换cmp和mp
获取 O(logn)
int x = 0;
mp[0] = "STL";
cout << "输出map中有多少个键值对" << mp.size() << '\n';
cout << "判断map中x键有多少个" << mp.count(x) << '\n';
cout << "判断map中x键是否存在" << mp.contains(x) << '\n'; // 返回bool类型
auto [a, b] = *mp.begin(); // 获取map中第一个元素的键和值
int aa = mp.begin()->first; // 获取map中第一个元素的键
string bb = mp.begin()->second; // 获取map中第一个元素的值
auto pp = --mp.end();
auto pre = prev(pp); // 获取当前地址的前一个地址,不改变当前地址
pp--; //地址前移,改变当前地址
auto ne = next(pp); // 获取当前地址的后一个地址,不改变当前地址
pp++; //地址后移,改变当前地址
遍历
for (auto [c, str] : mp) { cout << c << ' ' << str << '\n'; }
for (auto v : mp) { cout << v.first << ' ' << v.second << '\n'; }
for (auto it = mp.begin(); it != mp.end(); ++it) {
cout << it->first << ' ' << it->second << '\n';
cout << (*it).first << ' ' << (*it).first << '\n';
}
// lower_bound, upper_bound 函数与set相同,map中查找的为键,这里不重打一遍了,参照set即可
// 判断时的注意事项
// 如果键111不存在,则会自动创建一个键{111, ""}, 这样判断会增加时间复杂度, 建议采用以下方法判断键值是否存在
if (mp[111] != "HT") {}
if (mp.contains(111)) {} //
if (mp.count(111)) {} //
// 获取两个元素之间的距离,时间复杂度O(n),使用算一下时间复杂度
cout << distance(mp.begin(), mp.end()) << '\n';
pair
定义
// 简化版结构体,即可以将不同的数据类型绑定在一起pair<first, second>
pair<int, double> pid; // 绑定变量
pair<int, int> pii{1, 1}; // 初始化值
pair<set<int>, vector<int>> psv; // 绑定STL容器,默认为空
pair<int, pair<int, string>> piis; // 绑定pair自身
调用
int n = 10;
vector<pair<int, int>> a(n);
for (int i = 0; i < n; ++i) { // 赋值
a[i] = pair{i * i, i * i}; // 统一修改
a[i].first = i * i; // .first即修改pair的第一个健值
a[i].second = i * i; // .first即修改pair的第一个健值
}
// 末尾插入操作格式
a.push_back({-1, -1}), a.emplace_back(-1, -1);
// 默认按第一个键值为关键词进行升序排序
sort(a.begin(), a.end());
// 二分查找a数组中第一个键值大于1的位置
int pos = lower_bound(a.begin(), a.end(), pair{1, -1}) - a.begin();
pair<int, pair<int, int>> piii{1, {-1, -1}};
piii.second.first = 0; // 将piii的第二个健值的第一个键值设为0
// 解包,用两个变量将pair中的值取出来
pair<int, int> s{4, 5};
int x, y;
tie(x, y) = s;
auto [xx, yy] = s;
cout << x << ' ' << y << '\n';
cout << xx << ' ' << yy << '\n';
tuple 元组
vector< tuple< int, int>>取法
int a,b;
vector<tuple<int,int>>tl;
for(int i=0; i<7; ++i) { cin>>a>>b; tl.emplace_back(a+b,-(i+1)); }
sort(tl.begin(),tl.end());
if (get<0>(tl[6]) > 8) { cout<<-get<1>(tl[6])<<"\n"; }
else { cout << 0 << "\n"; }
针对 tuple
// 定义
// 可以看成pair的推广,与pair不同的是可以绑定更多的异类值
tuple<int, int, int> tiii;
tuple<int, string, vector<int>, int> tisvi;
// 调用
tuple<int, int, int> tup{1, 2, 4};
cout << "输出tup元组的第一个值: " << get<0>(tup) << "\n";
cout << "输出tup元组的所有值: \n";
for (int i = 0; i < 3; ++i) { cout << get<0>(tup) << " \n"[i == 2]; }
// 其余操作与pair同理,不再过多赘述
vector<tuple<int, int, int>> tl;
int n = 5;
for (int i = 0; i < n; ++ i) {
int a, b, c;
cin >> a >> b >> c;
tl.emplace_back(a, b, c);
}
int len = tl.size();
for (int i = 0; i < len; ++ i) {
int a = get<0>(tl[i]);
int b = get<1>(tl[i]);
}
for (auto [a, b, c] : tl) {cout << a<<" " << b<<" " << c<<"\n";}
set
定义,内部默认单调升序
constexpr int N = 11;
set<int> st1; // 定义一个int类型的集合
set<vector<int>> st2; // 定义一个vector<int>类型的集合
set<pair<int, int>> st3; // 定义一个pair<int, int>类型的集合
set<int> st4{{1, 2, 2, 4}}; // 定义一个st4, 并插入元素1, 2, 2, 4
vector a = {1, 2, 2, 4};
set st5 = set{a}; // 定义一个st5, 将数组a中的元素全部放入set
vector<set<int>> st6(N); // 定义了N个set
set<int> st7[N]; // 定义了N个set,这么定义建议在全局定义
set<int, greater<>> st8; // 定义一个单调降序的set
插入操作
set<int> sti;
set<pair<int, int>> stp;
sti.insert(1), sti.emplace(1); // 插入一个元素
stp.insert({1, 2}), stp.emplace(1, 2); // 插入一个元素
sti.insert({1, 2, 3, 4, 5, 7}); // 一次插入多个元素
stp.insert({{1, 2}, {3, 4}, {5, 7}}); // 一次插入多个元素
获取值
auto posi1 = sti.begin(); // 获取sti中第一个元素的地址
int vali1 = *posi1; // 获取sti中第一个元素的值
auto posi2 = sti.rbegin();
auto posi3 = --sti.end();
auto posi4 = prev(sti.end()); // 获取sti中最后一个元素的地址
int vali2 = *posi2; // 获取sti中最后一个元素的值
auto posp1 = stp.begin(); // 获取stp中第一个元素的地址
auto valp1 = *posp1; // 获取stp中第一个元素的值, 类型为pair<int, int>
auto [x, y] = *posp1;
int xx = posp1->first, yy = posp1->second; // 将pair中的两个值取出
cout << x << ' ' << y << '\n';
cout << xx << ' ' << yy << '\n';
auto pp = --stp.end();
auto pre = prev(pp); // 获取当前地址的前一个地址,不改变当前地址
pp--; //地址前移,改变当前地址
auto ne = next(pp); // 获取当前地址的后一个地址,不改变当前地址
pp++; //地址后移,改变当前地址
删除
int n = 10;
set<int> st;
for (int i = 0; i < n; ++i) {
st.insert(i);
}
st.erase(st.begin()); // 删除第一个元素
st.erase(--st.end()); // 删除最后一个元素
st.erase(1); // 将1这个值删除
st.clear(); // 清空集合
// 遍历set, 集合元素中的值无法被修改
for (auto x : st) {
cout << x << ' ';
}
cout << '\n';
for (auto it = st.begin(); it != st.end(); ++it) {
cout << (*it) << "\n";
}
cout << '\n';
查询操作
int query = 20;
cout << st.count(query) << "\n"; // 查寻st集合中query元素数量
// cout << st.contains(query) << "\n"; // 查寻st集合中query元素是否存在,返回类型为bool
cout << st.size() << "\n"; // 返回集合大小
cout << st.empty() << '\n'; // 判断集合和是否为空
二分查找
constexpr int INF = 1e9;
st.insert({-INF, INF}); // 未插入边界时,使用||前面的方法,插入边界后可以使用||后面的方法
auto pos1 = st.lower_bound(query); // 查找集合中大于等于query的元素的地址
auto pos2 = st.upper_bound(query); // 查找集合中大于query的元素的地址
auto pos3 = --st.lower_bound(query); // 查找集合中小于query的元素的地址
auto pos4 = --st.upper_bound(query); // 查找集合中小于等于query的元素的地址
// 判断边界,
// !!!注意如果要进行删除操作,优先将pos为位置的值存下再删除,否则先删除后再取不是原来的值
if (pos1 == st.end() || *pos1 == INF) { cout << "st中不存在大于等于query的元素" << '\n'; }
if (pos2 == st.end() || *pos2 == INF) { cout << "st中不存在大于query的元素" << '\n'; }
if (query <= *st.begin() || *pos3 == -INF) { cout << "st中不存在小于query的元素" << '\n'; }
if (query < *st.begin() || *pos4 == -INF) { cout << "st中不存在小于等于query的元素" << '\n'; }
// eg.将st中的2改成5,只能通过先删除再添加的方式修改
st.erase(2);
st.insert(5);
// 更改操作
set<int> cst;
st = cst; // 将cst复制给st
st.swap(cst); // 交换cst和st
// 获取两个元素之间的距离,时间复杂度O(n),使用算一下时间复杂度
cout << distance(st.begin(), st.end()) << '\n';
queue
定义
queue<int> que; // 定义一个名为que的队列
queue<int> q{{1, 2, 3, 4}}; // 在q队列中插入初值
// 插入操作
que.push(1), que.emplace(2); // 单个插入
// 查询
cout << "返回队头元素: " << q.front() << "\n";
cout << "查询队内元素个数: " << q.size() << '\n';
cout << "查询队列是否为空: " << q.empty() << "\n"; // 返回bool类型
// 出队
q.pop(); // 将队头元素删除
// 清空队列
// 方法一: 单个出队,直至队列为空
while (q.size()) {
q.pop();
}
// 方法二:定义一个空队列,使其覆盖原队列
queue<int> cq;
q = cq;
优先队列
priority_queue<ll, vector<ll>, greater<ll>> q; // 升序
priority_queue<ll, vector<ll>> q; // 降序
deque
定义
deque<int> que; // 定义一个名为que的双端队列
deque<int> q{{1, 2, 3, 4}}; // 在q队列中插入初值
// 插入操作
que.push_front(1), que.emplace_front(2); // 单个队头插入
que.push_back(1), que.emplace_back(2); // 单个队尾插入
// 查询
cout << "返回队头元素: " << q.front() << "\n";
cout << "返回队尾元素: " << q.back() << "\n";
cout << "查询队内元素个数: " << q.size() << '\n';
cout << "查询队列是否为空: " << q.empty() << "\n"; // 返回bool类型
// 出队
q.pop_front(); // 将队头元素删除
q.pop_back(); // 将队尾元素删除
// 清空队列
// 方法一: 单个出队,直至队列为空
while (q.size()) {
q.pop_back();
}
// 方法二:定义一个空队列,使其覆盖原队列
deque<int> cq;
q = cq;
stack
定义
stack<int> stk; // 定义一个名为stk的队列
stack<int> s{{1, 2, 3, 4}}; // 在s栈中插入初值
// 插入操作
stk.push(1), stk.emplace(2); // 单个插入
// 查询
cout << "返回栈头元素: " << s.top() << "\n";
cout << "查询栈内元素个数: " << s.size() << '\n';
cout << "查询栈是否为空: " << s.empty() << "\n"; // 返回bool类型
// 出栈
s.pop(); // 将栈顶元素删除
// 清空栈
// 方法一: 单个出栈,直至栈为空
while (s.size()) {
s.pop();
}
// 方法二:定义一个空栈,使其覆盖原栈
stack<int> cs;
s = cs;
bitset
bitset 定义
constexpr int N = 22, num = 15;
const string str = "101010111";
bitset<N> bit1;// 指定大小时必须为常量
vector<bitset<N>> bit2(N); // 定义N个长度为N的bitset
bitset<N> bit3(num); // 将十进制数num放入bit3容器转换为二进制数
bitset<N> bit4(str); // 将01字符串str放入bit4容器转换为二进制数
// 运算符
// operator<> : 流运算符,这意味着你可以通过 cin / cout 进行输入输出
bitset<N> bit(31);
cin >> bit;
cout << bit << '\n';
// operator []: 访问其特定的一位。
for (int i = 0; i < N; ++i) { cout << bit[i]; } cout << '\n';
// operator== / != : 比较两个 bitset 内容是否完全一样。
cout << (bit == bit1) << " " << (bit != bit1) << '\n';
// operator &/&=/|/| =/^/^=/~: 进行按位与/或/异或/取反操作。
// bitset 只能与 bitset 进行位运算,若要和整型进行位运算,要先将整型转换为 bitset。
cout << (bit & bit1) << "\n";
cout << (bit | bit1) << "\n";
cout << (bit ^ bit1) << "\n";
cout << (~bit) << "\n";
bit &= bit1;
cout << "按位与: " << bit << '\n';
bit |= bit1;
cout << "按位或: " << bit << '\n';
bit ^= bit1;
cout << "按位异或: " << bit << '\n';
// operator <>/<<=/>>=: 进行二进制左移/右移。
cout << "左移: " << (bit << 1) << " 右移: " << (bit >> 1) << '\n';
bit >>= 1; cout << bit << "\n";
bit <<= 1; cout << bit << "\n";
成员函数
int pos = 1;
bool flag = false;
cout << "返回true的数量" << bit.count() << "\n";
cout << "返回bitset的大小" << bit.size() << '\n';
cout << "查询pos位置的值" << bit.test(pos) << '\n';
cout << "查询是否存在true" << bit.any() << '\n';
cout << "查询是否全为false" << bit.none() << '\n';
cout << "查询是否全为true" << bit.all() << '\n';
bit.set(); // 将bit全部设置为true
bit.set(pos, flag); // 将pos位置设置为flag
bit.reset(); // 将bit全部设置为false
bit.reset(pos); // 将pos位置设置为false
bit.flip(); // 翻转每一位
bit.flip(pos); // 翻转pos上的数
string sbit = bit.to_string(); // 转换成的字符串表达
LL ubit = bit.to_ullong(); // 转换成unsigned long long类型
// 返回 bitset 第一个 true 的下标,若没有 true 则返回 bitset 的大小
int fpos = bit._Find_first();
// 返回 pos 后面(下标严格大于 pos 的位置)第一个 true 的下标,
// 若 pos 后面没有 true 则返回 bitset 的大小
int npos = bit._Find_next(pos);
// 第k位数,下面三种等效
int n=5,k=1,x=0;
n>>k&1;
// lowbit(x);
x&(-1);
x&(~x+1);
算法基础
前缀和 & 差分
一维前缀和
auto prefix = [&](vector<ll> &a, int lena) {
vector<ll> sa(lena + 1);
for (int i = 1; i <= lena; ++ i) {
sa[i] = sa[i - 1] + a[i];
}
return sa;
};
auto get = [&](vector<ll> &sa, int xb, int xe) {
ll res = sa[xe] - sa[xb - 1];
return res;
};
一维差分
auto dif = [&](vector<ll> &a, int lena) {
vector<ll> da(lena + 1);
for (int i = 1; i <= lena; ++ i) {
da[i] = a[i] - a[i - 1];
}
return da;
};
auto add = [&](vector<ll> &da, int s, int t, ll n) {
da[s] += n;
da[t + 1] -= n;
};
二维前缀和
auto prefix = [&](vector<vector<ll>> &a, int lena, int lenai) {
vector<vector<ll>> sa(lena + 1, vector<ll>(lenai + 1));
for (int i = 1; i <= lena; ++ i) {
for (int j = 1; j <= lenai; ++ j) {
sa[i][j] = a[i][j] + sa[i - 1][j] + sa[i][j - 1] - sa[i - 1][j - 1];
}
}
return sa;
};
auto get = [&](vector<vector<ll>> &sa, int xb, int yb, int xe, int ye) {
ll res = sa[xe][ye] - sa[xe][yb - 1] - sa[xb - 1][ye] + sa[xb - 1][yb - 1];
return res;
};
二维差分
auto dif = [&](vector<vector<ll>> &a, int lena, int lenai) {
vector<vector<ll>> da(lena + 1, vector<ll>(lenai + 1));
for (int i = 1; i <= lena; ++ i) {
for (int j = 1; j <= lenai; ++ j) {
da[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
}
}
return da;
};
auto add = [&](vector<vector<ll>> &da, int si, int sj, int ti, int tj, ll x) {
int n = da.size(), m = da[si].size();
da[si][sj] += x;
if (tj + 1 < m) da[si][tj + 1] -= x;
if (ti + 1 < n) da[ti + 1][sj] -= x;
if (ti + 1 < n && tj + 1 < m)da[ti + 1][tj + 1] += x;
};
二分
ll l = 1, r = inf;
while (l <= r) {
ll mid = (l + r) >> 1;
if (check(mid)) {
r = mid - 1;
} else {
l = mid + 1;
}
}
三分
ll n, b;
cin >> n >> b;
ll x = 0;
auto f = [&](ll x) {
ll left = (b + b + x - 1ll) * x / 2ll;
ll right = (b + b + n - 1ll) * n / 2ll - left;
return abs(left - right);
};
ll l = 0, r = n;
ll d1 = inf, d2 = inf;
while (l <= r) {
ll lm = l + (r - l) / 3;
ll rm = r - (r - l) / 3;
d1 = f(lm);
d2 = f(rm);
if (d1 <= d2) {
r = rm - 1;
} else {
l = lm + 1;
}
}
ll ans = min(d1, d2);
cout << ans << "\n";
struct BigInt {
std::vector<char> v;
BigInt(int x = 0) : v{} {
do v.push_back(x % 10); while (x /= 10);
}
BigInt(std::string &x) : v{} {
assert(size(x) != 0);
for (int i = (int)size(x) - 1; i >= 0; --i) {
v.push_back(x[i] - '0');
}
}
BigInt &operator=(int x) {
v.clear();
do v.push_back(x % 10); while (x /= 10);
return *this;
}
BigInt &operator=(const BigInt &x) {
v.resize(x.v.size());
memcpy(const_cast<char *>(v.data()), x.v.data(), x.v.size() * sizeof(char));
return *this;
}
friend bool operator==(const BigInt &a, const BigInt &b) {
if (size(a.v) == size(b.v)) {
int idx = 0;
while (idx < (int)size(a.v) && a.v[idx] == b.v[idx]) idx++;
return idx < (int)size(a.v);
} else {
return false;
}
}
friend bool operator!=(const BigInt &a, const BigInt &b) {
return !(a == b);
}
friend bool operator<(const BigInt &a, const BigInt &b) {
if (size(a.v) == size(b.v)) {
int idx = size(a.v) - 1;
while (idx >= 0 && a.v[idx] == b.v[idx]) idx--;
return idx >= 0 && a.v[idx] < b.v[idx];
}
return size(a.v) < size(b.v);
}
friend bool operator<=(const BigInt &a, const BigInt &b) {
if (size(a.v) == size(b.v)) {
int idx = size(a.v) - 1;
while (idx >= 0 && a.v[idx] == b.v[idx]) idx--;
return idx == -1 || a.v[idx] <= b.v[idx];
}
return size(a.v) < size(b.v);
}
friend bool operator>(const BigInt &a, const BigInt &b) {
if (size(a.v) == size(b.v)) {
int idx = size(a.v) - 1;
while (idx >= 0 && a.v[idx] == b.v[idx]) idx--;
return idx >= 0 && a.v[idx] > b.v[idx];
}
return size(a.v) > size(b.v);
}
friend bool operator>=(const BigInt &a, const BigInt &b) {
if (size(a.v) == size(b.v)) {
int idx = size(a.v);
while (idx >= 0 && a.v[idx] == b.v[idx]) idx--;
return idx == -1 || a.v[idx] >= b.v[idx];
}
return size(a.v) > size(b.v);
}
BigInt &operator+=(const BigInt &x) & {
int n = std::max<int>(size(v), size(x.v)), tmp = 0;
bool flag = false;
for (int i = 0; i < n; ++i) {
if (i >= (int)size(v)) v.push_back(0);
if (i < (int)size(x.v)) v[i] += x.v[i];
if (flag) v[i] += 1, flag = false;
if (v[i] >= 10) v[i] %= 10, flag = true;
}
if (flag) v.push_back(1);
return *this;
}
BigInt &operator-=(const BigInt &x) & {
assert(*this >= x);
bool flag = false;
for (int i = 0; i < (int)size(v); ++i) {
if (i < (int)size(x.v)) v[i] -= x.v[i];
if (flag) v[i] -= 1, flag = false;
if (v[i] < 0) v[i] += 10, flag = true;
}
while (size(v) > 1 && v.back() == 0) v.pop_back();
return *this;
}
BigInt &operator*=(const int &x) & {
int tmp = 0;
for (int i = 0; i < size(v); ++i) {
tmp += (int)x * v[i];
v[i] = tmp % 10;
tmp /= 10;
}
while (tmp) {
v.push_back(tmp % 10);
tmp /= 10;
}
return *this;
}
BigInt &operator*=(const BigInt &x) & {
BigInt result;
result.v.resize(size(v) + size(x.v));
for (int i = 0; i < (int)size(v); ++i) {
for (int j = 0; j < (int)size(x.v); ++j) {
result.v[i + j] += v[i] * x.v[j];
result.v[i + j + 1] += result.v[i + j] / 10;
result.v[i + j] %= 10;
}
}
while (size(result.v) > 1 && result.v.back() == 0) result.v.pop_back();
return *this = result;
}
BigInt &operator/=(const int &x) & {
int r = 0;
for (int i = size(v) - 1; i >= 0; --i) {
r = r * 10 + v[i];
v[i] = r / x;
r %= x;
}
while (size(v) > 1 && v.back() == 0) v.pop_back();
return *this;
}
int operator%=(const int &x) {
int r = 0;
for (int i = size(v) - 1; i >= 0; --i) {
r = r * 10 + v[i];
r %= x;
}
return r;
}
friend BigInt operator+(BigInt a, const BigInt &b) {
return a += b;
}
friend BigInt operator-(BigInt a, const BigInt &b) {
return a -= b;
}
friend BigInt operator*(BigInt a, const int &b) {
return a *= b;
}
friend BigInt operator*(BigInt a, const BigInt &b) {
return a *= b;
}
friend BigInt operator/(BigInt a, const int &b) {
return a /= b;
}
friend int operator%(BigInt a, const int &b) {
return a %= b;
}
friend std::istream &operator>>(std::istream &is, BigInt &a) {
std::string str;
is >> str;
a = BigInt(str);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const BigInt &a) {
for (int i = a.v.size() - 1; i >= 0; --i) os << (char)(a.v[i] + '0');
return os;
}
};
搜索
BFS
Breadth First Search 广度优先搜索
每次都尝试访问同一层的节点。 如果同一层都访问完了,再访问下一层。
class Point { // 点类,重载了点的加减法和输入输出,并且可以直接sort
public:
int x, y;
Point () {}
Point (int x, int y) : x(x), y(y) {}
// 重载见计算几何
};
int main() {
vector<Point> d = {{-1,0},{1,0},{0,-1},{0,1}};
int n, m; cin >> n >> m;
Point be, ed;
vector<vector<int>> g(n + 1, vector<int>(m + 1, 1));
vector<vector<int>> dp(n + 1, vector<int>(m + 1)); // dp[i][j]等于1表示该点能到
auto check = [&](Point p) { };// 用于判断点是否在范围内
auto bfs = [&](Point be) {
queue<Point> q; dp[be.x][be.y] = 1; q.push(be);
while (q.size()) {
auto t = q.front(); q.pop();
for (int i = 0; i < 4; i ++ ) {
Point p = t + d[i];
if (check(p) && g[p.x][p.y] && dp[p.x][p.y] == 0)
dp[p.x][p.y] = 1; q.push(p);
}
}
};
bfs(be);
}
动态规划(DP)
动态规划基础
最大子段和 mss
auto mss = [&](vector<ll> &il, int l, int r) { // O(n)
ll res = -1e9, sum = 0;
for (int i=l; i<r; ++i) {
if (sum < 0) {
sum = il[i];
} else {
sum += il[i];
}
res = max(sum, res);
}
return res;
};
最长上升子序列 lis
auto lis =[&](vector<int> &il) { // O(nlogn)
int fn = il.size();
vector<int> q(fn);
int len = 0;
q[0] = -2e9;
for (int i = 0; i < fn; ++i) {
int l = 0, r = len ;
while (l <= r) {
int mid = (l + r) >> 1;
if (q[mid] < il[i]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
len = max(len, l);
q[l] = il[i];
}
return len;
};
最长公共子序列 lcs
auto lcs = [&](string &a, string &b) { // O(n**2)
int lena = a.size();
int lenb = b.size();
vector<vector<int>> f(lena + 1, vector<int>(lenb + 1));
vector<vector<int>> pre(lena + 1, vector<int>(lenb + 1));
for (int i = 0; i < lena; ++ i) {
for (int j = 0; j < lenb; ++ j) {
if (a[i] == b[j]) {
f[i + 1][j + 1] = f[i][j] + 1;
pre[i + 1][j + 1] = 1;
} else {
if (f[i + 1][j] > f[i][j + 1]) { // left
pre[i + 1][j + 1] = 2;
} else { // up
pre[i + 1][j + 1] = 3;
}
f[i + 1][j + 1] = max(f[i + 1][j], f[i][j + 1]);
}
}
}
// return f[lena][lenb];
int nans = f[lena][lenb];
string sans = "";
int i = lena, j = lenb;
while (i > 0 && j > 0) {
if (pre[i][j] == 1) {
sans = a[i - 1] + sans;
i--;
j--;
} else if (pre[i][j] == 2) {
j--;
} else if (pre[i][j] == 3) {
i--;
}
}
return sans;
};
最长公共子串
string lcs(string &a, string &b) {
int lena = a.size();
int lenb = b.size();
vector<vector<int>> f(lena + 1, vector<int>(lenb + 1));
vector<vector<int>> pre(lena + 1, vector<int>(lenb + 1));
int maxlen = 0, mi, mj;
for (int i = 0; i < lena; ++ i) {
for (int j = 0; j < lenb; ++ j) {
if (a[i] == b[j]) {
f[i + 1][j + 1] = f[i][j] + 1;
pre[i + 1][j + 1] = 1;
if (f[i + 1][j + 1] > maxlen) {
mi = i + 1;
mj = j + 1;
}
} else {
if (f[i + 1][j] > f[i][j + 1]) { // left
pre[i + 1][j + 1] = 2;
} else { // up
pre[i + 1][j + 1] = 3;
}
// f[i + 1][j + 1] = max(f[i + 1][j], f[i][j + 1]);
}
}
}
int nans = f[lena][lenb];
string res = "";
int i = mi, j = mj;
while (i > 0 && j > 0) {
if (pre[i][j] == 1) {
res = a[i - 1] + res;
i--; j--;
} else if (pre[i][j] == 2) {
j--;
} else if (pre[i][j] == 3) {
i--;
}
if (f[i][j] == 0) break;
}
return res;
};
背包
01背包
for (int i = 1; i <= n; i++)
for (int l = W; l >= w[i]; l--)
f[l] = max(f[l], f[l - w[i]] + v[i]);
完全背包
#include <iostream>
using namespace std;
constexpr int MAXN = 1e4 + 5;
constexpr int MAXW = 1e7 + 5;
int n, W, w[MAXN], v[MAXN];
long long f[MAXW];
int main() {
cin >> W >> n;
for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
for (int i = 1; i <= n; i++)
for (int l = w[i]; l <= W; l++)
if (f[l - w[i]] + v[i] > f[l]) f[l] = f[l - w[i]] + v[i]; // 核心状态方程
cout << f[W];
return 0;
}
分组背包
for (int k = 1; k <= ts; k++) // 循环每一组
for (int i = m; i >= 0; i--) // 循环背包容量
for (int j = 1; j <= cnt[k]; j++) // 循环该组的每一个物品
if (i >= w[t[k][j]]) // 背包容量充足
dp[i] = max(dp[i],
dp[i - w[t[k][j]]] + c[t[k][j]]); // 像0-1背包一样状态转移
多重背包
for (int i = 1; i <= n; i++) {
for (int weight = W; weight >= w[i]; weight--) {
// 多遍历一层物品数量
for (int k = 1; k * w[i] <= weight && k <= cnt[i]; k++) {
dp[weight] = max(dp[weight], dp[weight - k * w[i]] + k * v[i]);
}
}
}
树形DP
通过 dfs,在返回上一层时更新当前结点的最优解。
vector<ll> w(n + 1); // w[i] 表示节点 i 的 点权
vector<ll> dp(n + 1, N); // dp[i] 表示当前节点所能达到的 最大值
vector<vector<int>> adj(n + 1, vector<int>(0)); // 邻接表
auto transition = [&](int child, int father) {
if (dp[child] > w[father]) {
dp[father] = min(dp[father], (w[father] + dp[child]) / 2ll);
} else {
dp[father] = min(dp[father], dp[child]);
}
};
auto dfs = [&](auto self, int cur, int father) -> void {
for (auto child : adj[cur]) {
if (child == father) continue; // 防止往回遍历
self(self, child, cur);
transition(child, cur);
}
};
dfs(dfs, 1, -1);
字符串
字符串哈希
constexpr ll P = 131; // 基底,即多项式哈希的进制数
constexpr int lem = 2; // 多值哈希的模数个数
class Hash { public: vector<ll> n = vector<ll> (lem + 1); };
int main() {
vector<ll> mod = {0ll, (ll)1e9 + 7, (ll)1e9 + 9}; // 模数
vector<vector<ll>> p(lent + 1, vector<ll>(lem + 1, 1)); // 位权
for (int i = 1; i <= lent; ++ i)
for (int j = 1; j <= lem; ++ j)
p[i][j] = (p[i - 1][j] * P) % mod[j];
auto hashing = [&](string a, int len) { // 哈希化
vector<Hash> h(len + 1);
for (int i = 1; i <= len; ++ i)
for (int j = 1; j <= lem; ++ j)
h[i].n[j] = (h[i - 1].n[j] * P + a[i - 1]) % mod[j];
return h;
};
auto get = [&](const vector<Hash> &h, int l, int r) { // 得到哈希值,注意是闭区间
Hash res;
for (int j = 1; j <= lem; ++ j) {
res.n[j] = (h[r].n[j] - h[l - 1].n[j] * p[r - l + 1][j] % mod[j] + mod[j]) % mod[j];
}
return res;
};
auto equal = [&](Hash h1, Hash h2) { // 判断两个哈希值是否相等
for (int j = 1; j <= lem; ++ j) { if (h1.n[j] != h2.n[j]) return 0; }
return 1;
};
}
KMP
int n = 0;
string s, t;
cin >> s >> t;
int lens = s.size(), lent = t.size();
string res = s, ret = t;
reverse(res.begin(), res.end());
reverse(ret.begin(), ret.end());
string str = s + '#' + t;
string restr = res + '#' + ret;
int lenst = str.size();
vector<int> pre(lenst + 1), repre(lenst + 1);
vector<tuple<int, char>> ans;
auto f = [&](string &s, vector<int> &pre, int lenall) {
for (int i = 1; i < lenall; ++ i) {
int len = pre[i - 1];
while (len != 0 && s[i] != s[len]) {
len = pre[len - 1];
}
if (s[i] == s[len]) {
pre[i] = len + 1;
}
}
};
f(str, pre, lenst);
f(restr, repre, lenst);
for (int i = lens; i < lenst - 1; ++ i) {
int cur = i - lens;
int j = lenst - cur - 2;
if (pre[i] + repre[j] == lens) {
n++;
ans.emplace_back(cur, str[i + 1]);
}
}
cout << n << "\n";
sort(ans.begin(), ans.end());
for (auto [a, b] : ans) {
cout << a << " " << b << "\n";
}
function<vector<int>(string)> kmp = [&](string s) {
int n = s.size();
s = ' ' + s;
vector<int> nxt(n + 1);
for(int i = 2, j = 0; i <= n; i++ ) {
while(j && s[j + 1] != s[i]) {
j = nxt[j];
}
if(s[j + 1] == s[i]) {
j++;
}
nxt[i] = j;
}
return nxt;
};
数学
位运算
异或
异或及其性质
异或在C++中的运算符是 ^ (Shift + 6)
异或可以理解为按位不进位加法
1.异或的逆运算就是异或本身 如果 a $ \otimes $ b = c ,那么 c $ \otimes $ b = a
2.异或满足交换律 即 a $ \otimes $ b == b $ \otimes $ a
3.异或满足结合律 即 (a $ \otimes $ b) $ \otimes $ c == a $ \otimes $ (b $ \otimes $ c)
4.异或满足分配律 即 a $ \otimes $ (b & c) == (a $ \otimes $ b) & (a $ \otimes $ c)
对于普通加法可以用高斯定律 sn = (1 + n) * n / 2 快速计算1~n的值
对于异或运算来说也有快速计算1~n各数的异或和的方法,即:
异或前缀和
\( s(n)为1到n的数的异或和 \)
\( s(n) = \begin{cases} 1, ~~~ n \% 4 == 1 \\ 0, ~~~ n \% 4 == 3 \\ n, ~~~ n \% 4 == 0 \\ n + 1, ~~~ n \% 4 == 2 \\ \end{cases} \)
代码实现如下:
auto xorprefix = [&](ll n) {
int flag = n % 4;
if (flag == 0) {
return n;
} else if (flag == 1) {
return 1;
} else if (flag == 2) {
return n + 1;
} else if (flag == 3) {
return 0;
}
};
快速幂
ll power(ll a, ll b, ll mod = mod) {
ll res = 1;
while (b) {
if (b & 1) {
res = (ll)res * a % mod;
}
a = (ll)a * a % mod;
b >>= 1;
}
return res;
}
数论
简化公式
\( \sum\limits_{k = 1}^{n} k = \frac{n(n + 1)}{2} \)
\( \sum\limits_{k = 1}^{n} k^{2} = \frac{n(n + 1)(2 n + 1)}{6} \)
\( \sum\limits_{k = 1}^{n} k^{3} = (\sum\limits_{k = 1}^{n} k)^{2} = \frac{ n^{2} (n + 1)^{2} }{4} \)
\( \sum\limits_{k = 1}^{n} k^{4} = \frac{n(n+1)(2n+1)(3n^2+3n-1)}{30} \)
数论基础
整除
\( a \vert b ,表示a是b的因子,即b可被a整除 \)
积性函数
定义
\( 若函数f(n), 满足f(1) = 1, 且 \forall x, y \in N^{*}, gcd(x, y) = 1 都有 f(xy) = f(x)f(y),则 f(n)\)为积性函数
\( 若函数f(n), 满足f(1) = 1, 且 \forall x, y \in N^{*} 都有 f(xy) = f(x)f(y),则 f(n)\)为完全积性函数
性质
\( 若 f(x) 和 g(x) 均为积性函数,则以下函数也为积性函数: \)
\( h(x) = f(x^{p}) \)
\( h(x) = f^{p}(x) \)
\( h(x) = f(x)g(x) \)
\( h(x) = \sum\limits_{d \vert x} f(d)g(\frac{x}{d}) \)
质数
Miller–Rabin 素性测试
二次探测定理
\( 如果 p 是奇质数,则 x^{2} \equiv 1 ~ (mod ~ p) 的解为 x \equiv 1 ~ (mod ~ p)或者 x \equiv p - 1 ~ (mod ~ p) \)
bool Miller_Rabin(long long p) { // 判断素数
if (p < 2) return 0;
if (p == 2) return 1;
if (p == 3) return 1;
long long d = p - 1, r = 0;
while (!(d & 1)) ++r, d >>= 1; // 将d处理为奇数
for (long long k = 0; k < 10; ++k) {
long long a = rand() % (p - 2) + 2;
long long x = power(a, d, p);
if (x == 1 || x == p - 1) continue;
for (int i = 0; i < r - 1; ++i) {
x = (__int128)x * x % p;
if (x == p - 1) break;
}
if (x != p - 1) return 0;
}
return 1;
}
long long Pollard_Rho(long long x) {
long long s = 0, t = 0;
long long c = (long long)rand() % (x - 1) + 1;
int step = 0, goal = 1;
long long val = 1;
for (goal = 1;; goal *= 2, s = t, val = 1) { // 倍增优化
for (step = 1; step <= goal; ++step) {
t = ((__int128)t * t + c) % x;
val = (__int128)val * abs(t - s) % x;
if ((step % 127) == 0) {
long long d = gcd(val, x);
if (d > 1) return d;
}
}
long long d = gcd(val, x);
if (d > 1) return d;
}
}
求最大质因子
ll max_factor = 0;
void fac(ll x) {
if (x <= max_factor || x < 2) return;
if (Miller_Rabin(x)) { // 如果x为质数
max_factor = max(max_factor, x); // 更新答案
return;
}
long long p = x;
while (p >= x) p = Pollard_Rho(x); // 使用该算法
while ((x % p) == 0) x /= p;
fac(x), fac(p); // 继续向下分解x和p
}
求所有质因子
std::vector<long long> factor(long long n) {
if (n == 1) return {};
std::vector<long long> g, d;
d.push_back(n);
while (!d.empty()) {
auto v = d.back();
d.pop_back();
auto rho = pollard_rho(v);
if (rho == v) {
g.push_back(rho);
} else {
d.push_back(rho);
d.push_back(v / rho);
}
}
std::sort(g.begin(), g.end());
return g;
}
最大公约数
扩展欧几里得算法
扩展欧几里得算法(Extended Euclidean algorithm, EXGCD),常用于求 ax+by=gcd(a,b) 的一组可行解。
ll exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1, y = 0;
return a;
} else {
ll d = exgcd(b, b%a, x, y);
ll t = x;
x = y;
y = t - a / b * y1;
return d;
}
}
欧拉函数
定义
欧拉函数,即 $ \phi(n) $,表示的是小于等于n的和n互质的数的个数。
性质
- $ 欧拉函数,是积性函数。$
$ 即对任意满足gcd(a,b) == 1的整数a,b,有 \phi(ab) = \phi(a)\phi(b) $
$ 特别的,当n是奇数时 \phi(2n) = \phi(n) $ - $ n = \sum\limits_{d \vert n} \phi(d)$
- \(若 n = p^{k},其中p是质数,那么 \phi(n) = p^{k} - p^{k-1}\)
- $ 由唯一分解定理,设 n = \prod\limits_{i = 1}^{s} (p_{i}^{k_{i}}) ,其中p_{i}是质数,有 \phi(i) = n * \prod\limits_{i = 1}^{s} \frac{p_{i} - 1}{p_{i}}$
- $ 对任意不全为0的整数m,n,\phi(mn)\phi(gcd(m, n)) = \phi(m)\phi(n)\phi(gcd(m, n)) $
ll phi(ll n) {
ll ans = n;
for (ll i = 2; i * i <= n; i++) {
if (n % i == 0) {
ans = ans / i * (i - 1ll);
while (n % i == 0) n /= i;
}
}
if (n > 1ll) ans = ans / n * (n - 1ll);
return ans;
}
如果是多个数的欧拉函数值,可以利用后面会提到的线性筛法来求得。 详见:筛法求欧拉函数
欧拉定理
与欧拉函数紧密相关的一个定理就是欧拉定理。其描述如下:
$ 若gcd(a, m) = 1,则 a^{\phi(m)} \equiv 1 (mod m)$
扩展欧拉定理
筛法
线性筛法
constexpr int maxn = 1e6;
int pnl[maxn + 10], cnt;//pnl
bool st[maxn + 10]; //索引为质数值就是0
void init_primes() {
st[0] = 1;
st[1] = 1;
for (int i = 2; i <= maxn; ++ i) {
if (st[i] == 0) pnl[cnt++] = i;
for (int j = 0; pnl[j] <= maxn / i; ++j) {
st[pnl[j] * i] = 1;
if (i % pnl[j] == 0) break;
}
}
}
注意到这个筛法还能求每个数的最小质因子
int minp[maxn]; //值为该索引的最小的质因子
void init_primes() {
iota(minp, minp + maxn, 0);
for (int i=2; i <= maxn; ++i) {
if (minp[i] == i) { pnl[cnt++] = i; }
for (int j=0; pnl[j] <= maxn / i; ++j) {
minp[pnl[j] * i] = min(minp[pnl[j] * i], pnl[j]);
if (i % pnl[j] == 0) { break; }
}
}
}
筛法求欧拉函数
constexpr int N = 1e5;
vector<int> pri;
bool not_prime[N];
int phi[N];
void pre(int n) {
phi[1] = 1;
for (int i = 2; i <= n; i++) {
if (!not_prime[i]) {
pri.push_back(i);
phi[i] = i - 1;
}
for (int pri_j : pri) {
if (i * pri_j > n) break;
not_prime[i * pri_j] = true;
if (i % pri_j == 0) {
phi[i * pri_j] = phi[i] * pri_j;
break;
}
phi[i * pri_j] = phi[i] * phi[pri_j];
}
}
}
裴蜀定理
\( 对于二元方程ax + by = c \)
\( 当且仅当c = gcd(a, b)时 \)
\( x, y 存在整数解 \)
\( 当c \neq gcd(a, b) \)
\( x, y 不存在整数解,但有非整数解 \)
推广:
\(
一定存在整数x, y, 满足ax + by = gcd(a, b) * n
\)
再推广:
\(
一定存在整数\{ x_{i} \vert i \in [1, n] \},满足
\)
莫比乌斯反演
莫比乌斯函数
定义
\( \mu (n) = \begin{cases} 1 ~~~~~~~~~~~ n = 1 \\ (-1)^{s} ~~~ s为n的质因子个数 \\ 0 ~~~~~~~~~~~ n含有相同质因子 \\ \end{cases} \)
性质
\( \sum\limits_{d \vert n} \mu (d) = [n = 1] \)
\( \sum\limits_{d \vert gcd(i, j)} \mu (d) = [gcd(i, j) = 1] \)
\( \sum\limits_{d \vert n} \mu (d) \frac{n}{d} = \phi(n) \)
生成莫比乌斯函数的代码
constexpr ll N = 1e6;
int mu[N + 1];
int p[N + 1];
bool vis[N + 1];
int cnt;
void initmu () {
mu[1] = 1;
for (int i = 2; i <= N; ++ i) {
if (!vis[i]) {
p[++cnt] = i;
mu[i] = -1;
}
for (int j = 1; j <= cnt && i * p[j] <= N; ++ j) {
vis[i * p[j]] = 1;
if (i % p[j] == 0) {
mu[i % p[j]] = 0;
break;
}
mu[i * p[j]] = -mu[i];
}
}
}
例题
\( 已知n, m求\sum\limits_{i = 1}^{n} \sum\limits_{j = 1}^{m} lcm(i, j) (mod) \)
\( = \sum\limits_{d = 1}^{n} d \sum\limits_{k = 1}^{\lfloor \frac{n}{d} \rfloor} \mu(k) k^{2} \sum\limits_{i = 1}^{\lfloor \frac{n}{dk} \rfloor} i \sum\limits_{j = 1}^{\lfloor \frac{m}{dk} \rfloor} j \)
设
\( F(n, m) = \sum\limits_{k = 1}^{n} \mu(k) k^{2} \sum\limits_{i = 1}^{\lfloor \frac{n}{k} \rfloor} i \sum\limits_{j = 1}^{\lfloor \frac{m}{k} \rfloor} j \)
\( G(n, m) = \sum\limits_{i = 1}^{n} i \sum\limits_{j = 1}^{m} j \)
constexpr ll N = 1e7 + 10;
int mu[N + 1];
int p[N + 1];
ll s[N + 1];
bool vis[N + 1];
int cnt;
void initmu () {
mu[1] = 1;
for (int i = 2; i <= N; ++ i) {
if (!vis[i]) {
p[++cnt] = i;
mu[i] = -1;
}
for (int j = 1; j <= cnt && i * p[j] <= N; ++ j) {
vis[i * p[j]] = 1;
if (i % p[j] == 0) {
mu[i % p[j]] = 0;
break;
}
mu[i * p[j]] = -mu[i];
}
}
for (int i = 1; i <= N; ++ i) {
s[i] = (s[i - 1] + (ll)mu[i] * i * i % mod + mod) % mod;
}
}
ll G(ll n, ll m) {
return (n * (n + 1ll) / 2ll % mod) * (m * (m + 1ll) / 2ll % mod) % mod;
}
ll F(ll n, ll m) {
ll res = 0;
for (int l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
res = (res + (ll)(s[r] - s[l - 1]) * G(n / l, m / l) % mod + mod) % mod;
}
return res;
}
int calc (ll n, ll m) {
ll res = 0;
if (n > m) swap(n, m);
for (ll l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
res = (res + (ll)(r - l + 1) * (l + r) / 2ll % mod * F(n / l, m / l) % mod) % mod;
}
return res;
}
BSGS 大步小步算法 求离散对数
int gcd(int a, int b) { return a ? gcd(b % a, a) : b; }
int powmod(int a, int b, int p) {
int res = 1;
while (b > 0) {
if (b & 1) res = res * a % p;
a = a * a % p, b >>= 1;
}
return res;
}
// Finds the primitive root modulo p
int generator(int p) {
vector<int> fact;
int phi = p - 1, n = phi;
for (int i = 2; i * i <= n; ++i) {
if (n % i == 0) {
fact.push_back(i);
while (n % i == 0) n /= i;
}
}
if (n > 1) fact.push_back(n);
for (int res = 2; res <= p; ++res) {
bool ok = true;
for (int factor : fact) {
if (powmod(res, phi / factor, p) == 1) {
ok = false;
break;
}
}
if (ok) return res;
}
return -1;
}
// This program finds all numbers x such that x^k=a (mod n)
int main() {
int n, k, a;
scanf("%d %d %d", &n, &k, &a);
if (a == 0) return puts("1\n0"), 0;
int g = generator(n);
// Baby-step giant-step discrete logarithm algorithm
int sq = (int)sqrt(n + .0) + 1;
vector<pair<int, int>> dec(sq);
for (int i = 1; i <= sq; ++i)
dec[i - 1] = {powmod(g, i * sq * k % (n - 1), n), i};
sort(dec.begin(), dec.end());
int any_ans = -1;
for (int i = 0; i < sq; ++i) {
int my = powmod(g, i * k % (n - 1), n) * a % n;
auto it = lower_bound(dec.begin(), dec.end(), make_pair(my, 0));
if (it != dec.end() && it->first == my) {
any_ans = it->second * sq - i;
break;
}
}
if (any_ans == -1) return puts("0"), 0;
// Print all possible answers
int delta = (n - 1) / gcd(k, n - 1);
vector<int> ans;
for (int cur = any_ans % delta; cur < n - 1; cur += delta)
ans.push_back(powmod(g, cur, n));
sort(ans.begin(), ans.end());
printf("%zu\n", ans.size());
for (int answer : ans) printf("%d ", answer);
}
多项式与生成函数
普通生成函数
广义二项式定理
指数生成函数
有序数列的生成函数
狄利克雷生成函数(DGF)
定义
(即分子下标相乘等于分母的底数)
f(n), g(n)是两个积性函数,
\( (f * g)(n) = \sum\limits_{d \vert} \)
三个常用函数
\( 1.元函数 \epsilon(n) = [n = 1] \)
\( 2.常数函数 1(n) = 1 \)
\( 3.恒等函数 id(n) = n \)
常用卷积关系
\( 1.\sum\limits_{d \vert n} \mu(d) = [n = 1] ~~~ \Leftrightarrow ~~~ \mu * 1 = \epsilon \)
\( 2.\sum\limits_{d \vert n} \phi(d) = n ~~~~~~~~~~~~~ \Leftrightarrow ~~~ \phi * 1 = id \)
\( 3.\sum\limits_{d \vert n} \mu(d) \frac{n}{d} ~~~~~~~~~~~~~~~~~~ \Leftrightarrow ~~~ \mu * id = \phi \)
\( 4.f * \epsilon = f \)
\( 5.f * 1 \neq f \)
组合数学
排列组合
排列组合基础
下面介绍求组合数的方法
1.杨辉三角法
\( 根据 C_{n}^{m} = C_{n - 1}^{m} + C_{n - 1}^{m - 1} ~~~ 可O(n^{2})预处理C_{n}^{m}的值 \)
constexpr ll CN = 10000;
ll C[CN + 10][CN + 10];
// ll A[CN + 7][CN + 7];
// ll fact[CN + 7];
ll H[CN + 7];
void initc() { // combinatorics
// fact[1] = 1ll;
for (ll i = 0; i <= CN; ++i) {
// if (i > 1) fact[i] = fact[i - 1] % mod * i % mod;
for (int j = 0; j <= i; ++j) {
if (!j) {
C[i][j] = 1ll;
} else {
C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
}
// A[i][j] = C[i][j] % mod * fact[j] % mod;
}
}
}
2.公式法
\( 根据 C_{n}^{m} = \frac{n!}{m!(n-m)!} ~~~ 可O(n)预处理阶乘,再通过公式计算 \)
constexpr ll maxn = 10000;
ll fact[maxn + 2];
ll inv[maxn + 2];
void initfact() {
fact[0] = 1;
for (ll i = 1; i <= maxn; ++ i) {
fact[i] = fact[i - 1] * i % mod;
}
inv[maxn] = power(fact[maxn], mod - 2);
for (ll i = maxn - 1; i >= 1; -- i) {
inv[i] = inv[i + 1] * (i + 1ll) % mod;
}
}
ll C(int n, int m) {
if (m > n) {
return 0;
} else if (m == 0 || n == m) {
return 1;
} else {
if (n > maxn) {
ll res = 1, inv = 1;
for (ll k = 1; k <= m; ++ k) {
res = res * (n - k + 1ll) % mod;
inv = inv * k % mod;
}
res = res * power(inv, mod - 2) % mod;
return res;
} else {
return fact[n] * inv[m] % mod * inv[n - m] % mod;
}
}
}
\( C_{n}^{m} = C_{n - 1}^{m - 1} + C_{n - 1}^{m} \)
\(\sum\limits_{k = m}^{n} C_{k}^{m} = C_{n + 1}^{m + 1}\)
结论:对于C(n,k),若n&k == k 则c(n,k)为奇数,否则为偶数。
多重集
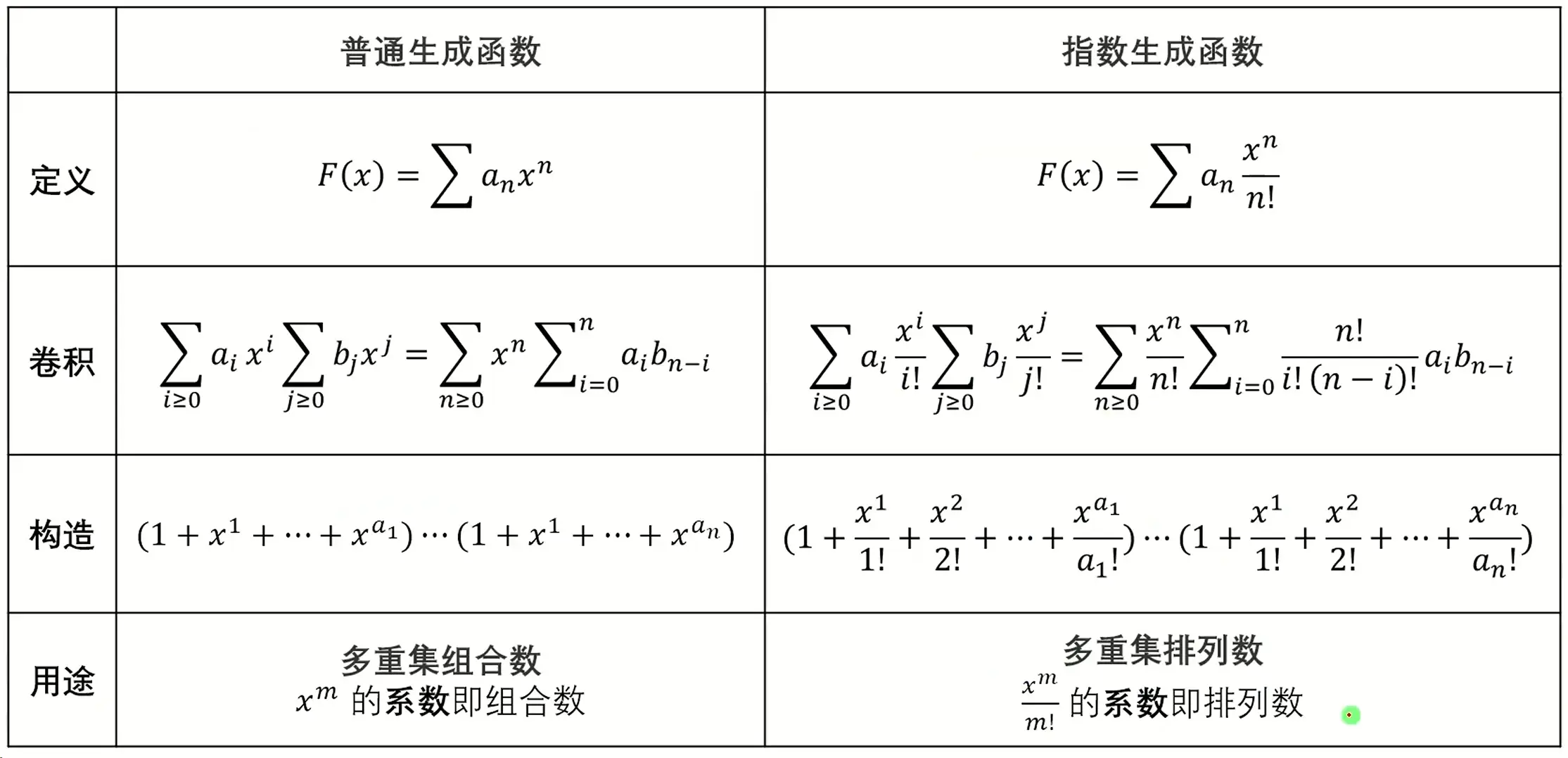
二项式定理
\( \tbinom{n}{m} = C_{n}^{m} = \frac{n!}{m!(n-m)!} \)
n个空位,分配m个人进去(可重复)
广义二项式定理
容斥原理
例题:求分母不超过n的所有最简真分数的个数与他们的和 (n <= 1e6)
显然有:
\( ans = \sum\limits_{a = 1}^{n} \sum\limits_{b = 1}^{a} ([b < a] * [gcd(a, b) == 1]) = (\sum\limits_{a = 1}^{n} \sum\limits_{b = 1}^{n} [gcd(a, b) == 1]) / 2 \)
那么只需求出n以内的互质对即可。即以1为最大公约数的数对
由容斥原理可以得知,先找到所有以1为公约数的数对,再从中剔除所有以1的倍数为公约数的数对,余下的数对就是以1为最大公约数的数对。即f(k)=以1为公约数的数对个数 - 以1的倍数为 公约数 的数对个数。
可以注意到,当(x,y)为互质时,(y-x,y)也互质。那么有这些最简真分数的和就是它们的个数除以2。
代码实现如下:
ll nn = 2e6;
cin >> nn;
vector<ll> f(nn + 1);// f[i] 表示 gcd == i 的情况有几种
for (ll k = nn; k >= 1; k--) {
f[k] = (nn / k) * (nn / k);//以k为公约数的数对
for (ll i = k + k; i <= nn; i += k) { //减去以k的倍数为公约数的数对
f[k] -= f[i];
}
}
ans1 = f[1] / 2;
ans2 = (double)ans1 / 2.0;
cout << ans1 << " " << ans2 << "\n";
卡特兰数
通项公式:
递推公式:
Catalan 特征:
从(0,0)到(n,n),不越过对角线,即任何时候,向上走的步数不能超过向右走的步数。
一种操作数不能超过另一种操作数,或者两种操作数不能有交集,这些操作的方案数通常是卡特兰数
Catalan 应用:
1.一个有n个0和n个1组成的字串,且所有的前缀字串满足1的个数不超过0的个数。这样的字串个数是多少?
2.包含n组括号的合法运算式的个数有多少?
3.一个栈的进栈序列为1,2,3,~,n,有多少个不同的出栈序列?
4.n个结点可构造多少个不同的二叉树?
5.在圆上选择2n个点,将这些点成对连接起来使得所得到的n条弦不相交的方法数?
6.通过连结顶点而将n+2边的凸多边形分成n个三角形的方法数?
博弈论
Bash Game
只有一堆 \(n\) 个物品,两个人轮流从这堆物品中取物,每次取 \([1, m]\),取走最后一个物品的人获胜。
若 \(n \% (m + 1) == 0\),先手必败,否则先手必胜
Nim Game
\(n\) 堆物品,每堆有 \(a_i\) 个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。取走最后一个物品的人获胜。
当且仅当
\(\oplus ai = 0\)
先手必败,否则先手必胜
K-Nim

Fibonacci Nim

Wythoff Game

有向图博弈
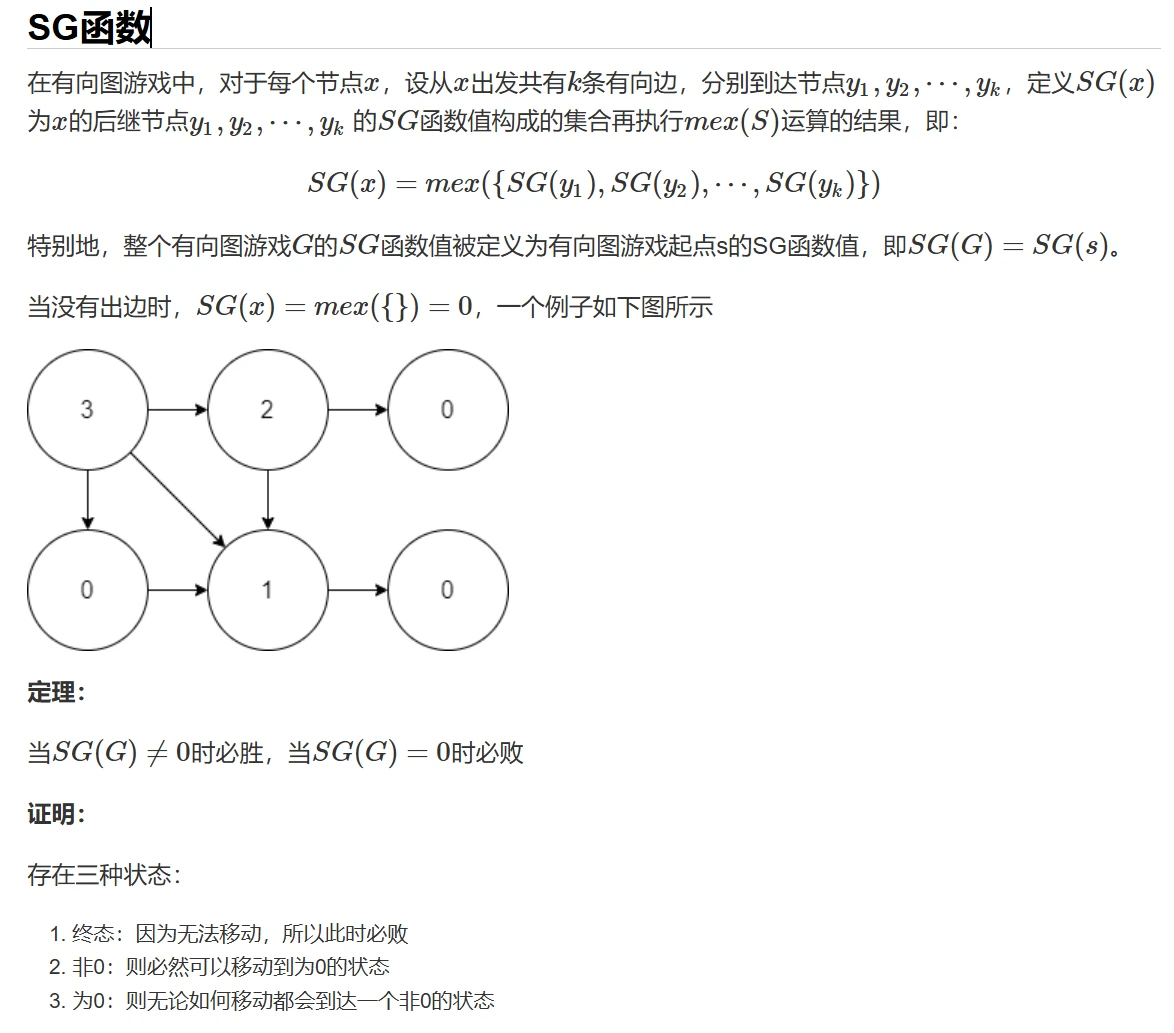

int SG[N];
int k;
int sg(int x) {
if (x < 0) return -1;
if (SG[x]) return SG[x];
set<int> s;
s.insert(sg(x - 1));
s.insert(sg(x - 2));
s.insert(sg(x - k));
for (int i = 0; ; i++) {
if (!s.count(i)) {
return SG[x] = i;
}
}
}
https://www.acwing.com/blog/content/13279/
线性代数
行列式
Double
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const int MAXN = 501;
const double EPS = 1e-5;
int n;
double A[MAXN][MAXN];
int main(void) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j)
scanf("%lf", &A[i][j]);
scanf("%lf", &A[i][n + 1]);
}
//Gauss 消元主体
for(int i = 1; i <= n; ++i) {
int tmp = i; //tmp 表示主元系数绝对值最大的行
for(int j = i + 1; j <= n; ++j)
if(fabs(A[tmp][i]) < fabs(A[j][i])) //打擂台找到绝对值最大的系数
tmp = j;
for(int j = 1; j <= n + 1; ++j)
swap(A[i][j], A[tmp][j]); //将该行与当前行交换
if(fabs(A[i][i]) <= EPS) {
//如果主元的绝对值最大也只是 0,则代表该元
//可以被前面的几个方程消去,矩阵不满秩,则无解
//注意 double 类型不能直接进行比较,可以用 EPS 比较法
printf("No Solution");
return 0;
}
double cur = A[i][i];
for(int j = 1; j <= n + 1; ++j) A[i][j] /= cur; //将该行主元系数化为 1
//枚举每一行,消去该行的主元
for(int j = 1; j <= n; ++j) {
if(j == i) continue;
double div = A[j][i];
for(int k = 1; k <= n + 1; ++k)
A[j][k] -= div * A[i][k];
}
}
for(int i = 1; i <= n; ++i)
printf("%.2f\n", A[i][n + 1]);
return 0;
}
Mod
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long ll;
const int MAXN = 1001;
const ll MOD = 1000000007;
ll inv(ll x) { //Fermat 小定理求逆元
ll ans = 1, p = MOD - 2;
while(p) {
if(p & 1) ans = (ans * x) % MOD;
x = (x * x) % MOD; p >>= 1;
}
return ans;
}
int n;
ll A[MAXN][MAXN];
int main(void) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j)
scanf("%lld", &A[i][j]);
A[i][n + i] = 1;
}
//Gauss 消元求矩阵的逆
for(int i = 1; i <= n; ++i) {
int tmp = i;
for(int j = i + 1; j <= (n << 1); ++j)
if(A[tmp][i] < A[j][i]) //打擂台找到绝对值最大的系数
tmp = j;
//判定矩阵不可逆,不解释
if(A[i][i] == 0) {
printf("No Solution");
return 0;
}
ll cur = inv(A[i][i]);
for(int j = 1; j <= (n << 1); ++j)
A[i][j] = (A[i][j] * cur) % MOD; //该行主元系数化为 1
//和 Gauss 消元一毛一样的套路 =v=
for(int j = 1; j <= n; ++j) {
if(i == j) continue;
ll div = A[j][i];
for(int k = 1; k <= (n << 1); ++k)
A[j][k] = ((A[j][k] - div * A[i][k]) % MOD + MOD) % MOD;
}
}
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j)
printf("%lld ", A[i][n + j]);
printf("\n");
}
return 0;
}
高斯消元
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
const double pi = acos(-1);
const double E = exp(1);
constexpr ll mod = 1e9 + 7;
// constexpr int inf = 0x3f3f3f3f;
constexpr ll inf = 0x3f3f3f3f3f3f3f3f;
bool sgn(ll n) {
return n < 0 ? 1 : 0;
}
class frac {
public:
ll n, d = 1; // 分子,分母
frac () {}
frac (ll n, ll d) : n(n), d(d) {}
frac operator+(const frac &f) const {
ll nn = n * f.d + d * f.n, dd = d * f.d;
ll g = gcd(nn, dd);
nn /= g, dd /= g;
return frac(nn, dd);
}
frac operator-(const frac &f) const {
ll nn = n * f.d - d * f.n, dd = d * f.d;
ll g = gcd(nn, dd);
nn /= g, dd /= g;
return frac(nn, dd);
}
frac operator*(const frac &f) const {
ll nn = n * f.n, dd = d * f.d;
ll g = gcd(nn, dd);
nn /= g, dd /= g;
return frac(nn, dd);
}
frac operator/(const frac &f) const {
ll nn = n * f.d, dd = d * f.n;
ll g = gcd(nn, dd);
if (sgn(dd)) g *= -1ll;
nn /= g, dd /= g;
return frac(nn, dd);
}
bool operator<(const frac &f) const { return n * f.d < d * f.n; }
bool operator==(const frac &f) const { return n == f.n && d == f.d; }
bool operator!=(const frac &f) const { return n != f.n || d != f.d; }
friend istream &operator>>(istream &is, frac &rhs) { return is >> rhs.n; }
friend ostream &operator<<(ostream &os, const frac &rhs) { return os << rhs.n << '/' << rhs.d; }
};
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n;
cin >> n;
vector<vector<frac>> a(n + 1, vector<frac>(n + 2));
for (int i = 1; i <= n; ++ i) {
for (int j = 1; j <= n + 1; ++ j) {
cin >> a[i][j];
}
}
auto gauss =[&](vector<vector<frac>> &a) {
for (int i = 1; i <= n; ++ i) {
int r = i;
for (int k = i; k <= n; ++ k) {
if (a[k][i].n == 0) {
r = k;
break;
}
}
if (r != i) swap(a[r], a[i]);
if (a[i][i].n == 0) return 0;
for (int j = n + 1; j >= i; -- j) {
a[i][j] = a[i][j] / a[i][i];
}
for (int k = i + 1; k <= n; ++ k) {
for (int j = n + 1; j >= i; -- j) {
a[k][j] = a[k][j] - a[k][i] * a[i][j];
}
}
}
for (int i = n - 1; i >= 1; -- i) {
for (int j = i + 1; j <= n; ++ j) {
a[i][n + 1] = a[i][n + 1] - a[i][j] * a[j][n + 1];
}
}
return 1;
};
if (gauss(a)) {
cout << "Yes\n";
for (int i = 1; i <= n; ++ i) {
cout << a[i][n + 1] << " \n"[i == n];
}
} else {
cout << "No\n";
}
}
数据结构(DS)
单调栈
class MS { // Monotone stack
public:
int n, top;
vector<ll> sta;
MS() {}
MS(int n) { init(n); };
void init(int n) {
this -> n = n;
top = 0;
sta.resize(n + 1, inf);
sta[0] = 0;
}
void insert(ll x) {
while (x <= sta[top]) {
top --;
}
sta[++top] = x;
}
void show() {
for (int i = 1; i <= top; ++ i) {
cout << sta[i] << " \n"[i == top];
}
}
};
并查集
class DSU {
public:
int n;
vector<int> dsu, dsus;
// dsu[i]存是 i 的祖宗结点
// dsus[i]存 i 所在图的大小
DSU() {}
DSU(int n) { init(n); }
void init(int n) {
this -> n = n;
dsu.resize(n + 1);
dsus.resize(n + 1, 1);
iota(dsu.begin(), dsu.end(), 0);
}
int find(int a) {
if (a == dsu[a]) {
return a;
} else {
dsu[a] = find(dsu[a]);
return dsu[a];
}
}
void merge(int a, int b) {
int x = find(a);
int y = find(b);
if (x != y) {
if (dsus[x] < dsus[y]) { swap(x, y); }
dsu[y] = x; dsus[x] += dsus[y];
}
}
// 由于未必路径压缩好了,所以求祖宗结点需调用find函数或者使用reboot()函数路径压缩
void reboot() {
for (int i = 1; i <= n; ++ i) {
int fa = find(dsu[i]);
dsu[i] = fa; dsus[i] = dsus[fa];
}
}
};
树状数组
树状数组是一种支持 单点修改 和 区间查询 的,代码量小的数据结构。
普通树状数组维护的信息及运算要满足 结合律 且 可差分 如加法(和)、乘法(积)、异或等。
\( \bullet 结合律:(x \circ y) \circ z = x \circ (y \circ z),其中 \circ 是一个二元运算符 \)
\( \bullet 可差分:具有逆运算的运算,即已知 x \circ y 和 x 可以求出 y。 \)
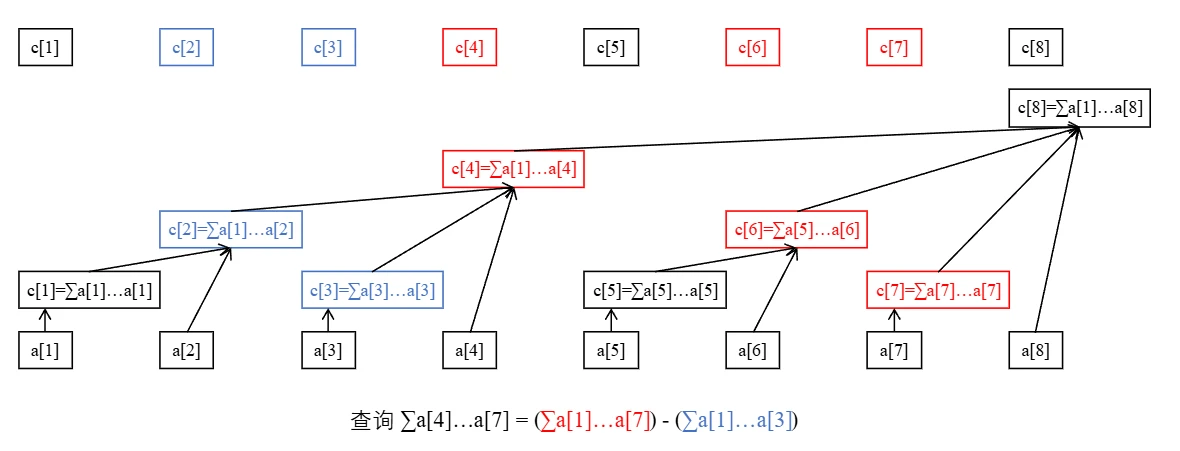
class BIT {
public:
int n;
vector<ll> t;
BIT() {}
BIT(int n) { init(n); }
void init(int n) {
this -> n = n;
t.resize(n + 1);
}
int lowbit(int x) {return x & (- x);};
// O(n)建树
void build(int n, vector<ll> &s) {
for (int i = 1; i <= n; ++ i) {
t[i] += s[i];
int fa = i + lowbit(i);
if (fa <= n) {
t[fa] += t[i];
}
}
}
void add (int x, int y) {
for (int pos = x; pos <= n; pos += lowbit(pos)) {
t[pos] += y;
}
}
ll query (int x) {
ll res = 0;
for(int pos = x; pos; pos -= lowbit(pos)) {
res += t[pos];
}
return res;
}
ll query (ll l, ll r) {
return query(r) - query(l - 1);
}
};
点修区查
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
int n, m;
cin >> n >> m;
vector<ll> a(n + 1);
for (int i = 1; i <= n; ++ i) cin >> a[i];
BIT bit(n);
bit.build(n, a);
for (int i = 1; i <= m; ++ i) {
int op;
cin >> op;
if (op == 1) {
ll x, k;
cin >> x >> k;
bit.add(x, k);
} else {
ll x, y;
cin >> x >> y;
ll ans = bit.query(x, y);
cout << ans << "\n";
}
}
}
区修点查
auto dif = [&](vector<ll> &a, int lena) {
vector<ll> da(lena + 1);
for (int i = 1; i <= lena; ++ i) {
da[i] = a[i] - a[i - 1];
}
return da;
};
int n, m;
cin >> n >> m;
vector<ll> a(n + 1);
for (int i = 1; i <= n; ++ i) cin >> a[i];
vector<ll> da = dif(a, n);
BIT bit(n);
bit.build(n, da);
for (int i = 1; i <= m; ++ i) {
int op;
cin >> op;
if (op == 1) {
ll x, y, k;
cin >> x >> y >> k;
bit.add(x, k);
bit.add(y + 1, -k);
} else {
ll x;
cin >> x;
ll ans = bit.query(x);
cout << ans << "\n";
}
}
线段树
class info {
public:
int l, r;
ll max;
ll min;
ll sum;
ll mss;
ll lmss;
ll rmss;
info () {}
info (int l, int r, ll m) { init(l, r, m); }
void init(int l, int r, ll m) {
this -> l = l;
this -> r = r;
this -> max = m;
this -> min = m;
this -> sum = m;
this -> mss = m;
this -> lmss = m;
this -> rmss = m;
}
};
class ST {
public:
int n;
vector<info> tr;
int ls(int x) { return x << 1; };
int rs(int x) { return x << 1 | 1; };
void pushup(info &t, info l, info r) {
t.max = max(l.max, r.max);
t.min = min(l.min, r.min);
t.sum = l.sum + r.sum;
t.lmss = max(l.lmss, l.sum + r.lmss);
t.rmss = max(r.rmss, r.sum + l.rmss);
t.mss = max(max(l.mss, r.mss), l.rmss + r.lmss);
};
ST() {}
ST(int n) { init(n); }
void init(int n) {
this -> n = n;
tr.resize(4 * n + 16);
}
void build(int l, int r, int p, vector<info> &s) {
tr[p] = info(l, r, s[l].max);
if (l == r) return ;
int mid = (l + r) >> 1;
build(l, mid, ls(p), s);
build(mid + 1, r, rs(p), s);
pushup(tr[p], tr[ls(p)], tr[rs(p)]);
}
void build(vector<info> &s) {
build(1, n, 1, s);
}
void change0(int u, int x, ll w) {
if (tr[u].l == tr[u].r) {
tr[u] = info(x, x, w);
return ;
}
int mid = (tr[u].l + tr[u].r) >> 1;
if (x <= mid) {
change0(ls(u), x, w);
} else {
change0(rs(u), x, w);
}
pushup(tr[u], tr[ls(u)], tr[rs(u)]);
}
void change(int x, int w) { change0(1, x, w); };
info query0(int u, int l, int r) {
if (l <= tr[u].l && tr[u].r <= r) return tr[u];
int mid = (tr[u].l + tr[u].r) >> 1;
if (r <= mid) return query0(ls(u), l, r);
if (l > mid) return query0(rs(u), l, r);
info T;
pushup(T, query0(ls(u), l, mid), query0(rs(u), mid + 1, r));
return T;
};
info query(int l, int r) { return query0(1, l, r); };
info inquire0(int u, ll x) {
if (tr[u].l == tr[u].r) {
return tr[u];
}
if (tr[ls(u)].max >= x) {
return inquire0(ls(u), x);
} else {
return inquire0(rs(u), x);
}
}
info inquire(ll x) {
return inquire0(1, x);
}
void show() {
for (int i = 1; i <= 2 * n - 1; ++ i) {
cout << tr[i].l << " ";
cout << tr[i].r << " ";
cout << tr[i].max << "\n";
}
}
};
int main() {
int n, q;
cin >> n >> q;
vector<ll> a(n + 1, 1);
vector<info> s(n + 1);
ST t(n);
t.build(s);
}
主席树
int idx = 1;
class info {
public:
int ls = 0, rs = 0;
int n = 0;
ll sum = 0;
};
class PST {
public:
int n = 0;
vector<info> tr;
vector<int> roots;
PST () {}
PST (int n) { init(n); }
void init(int n) {
this -> n = n;
roots.resize(n + 10);
tr.resize(30 * (n + 30));
}
void build(int &x, int l, int r) {
x = idx;
idx ++;
if (l == r) return ;
int m = (l + r) >> 1;
build(tr[x].ls, l, m);
build(tr[x].rs, m + 1, r);
}
void insert0(int x, int &y, int l, int r, int v, ll rv) {
y = idx;
idx ++;
tr[y] = tr[x];
tr[y].n ++;
tr[y].sum += rv;
if (l == r) return ;
int m = (l + r) >> 1;
if (v <= m) {
insert0(tr[x].ls, tr[y].ls, l, m, v, rv);
} else {
insert0(tr[x].rs, tr[y].rs, m + 1, r, v, rv);
}
}
void insert(int &i, int v, ll rv) {
insert0(roots[i - 1], roots[i], 1, n, v, rv);
}
ll query0(int x, int y, int l, int r, int k) {
if (l == r) return l;
int m = (l + r) >> 1;
int s = tr[tr[y].ls].n - tr[tr[x].ls].n;
if (k <= s) {
return query0(tr[x].ls, tr[y].ls, l, m, k);
} else {
return query0(tr[x].rs, tr[y].rs, m + 1, r, k - s);
}
};
ll query(int l, int r, int k) {
return query0(roots[l - 1], roots[r], 1, n, k);
}
ll querysum0(int x, int y, int l, int r, int k) {
if (l == r) {
ll t = (tr[y].sum - tr[x].sum) / ((ll)tr[y].n - tr[x].n);
return (ll)t * k;
}
int m = (l + r) >> 1;
int s = tr[tr[y].rs].n - tr[tr[x].rs].n;
if (s >= k) {
return querysum0(tr[x].rs, tr[y].rs, m + 1, r, k);
} else {
return querysum0(tr[x].ls, tr[y].ls, l, m, k - s) + tr[tr[y].rs].sum - tr[tr[x].rs].sum;
}
}
ll querysum(int l, int r, int k) {
return querysum0(roots[l - 1], roots[r], 1, n, k);
}
void show() {
for (int i = 0; i <= n; ++ i) {
if (roots[i] == 0) break;
cout << i << " " << roots[i] << "\n";
}
for (int i = 1; i <= idx; ++ i) {
cout << i << " [";
cout << tr[i].ls << ", ";
cout << tr[i].rs << "] ";
cout << tr[i].n << " ";
cout << tr[i].sum << " ";
cout << "\n";
}
}
};
ll f(ll n) { return n * (n + 1ll) * (n * 2ll + 1ll) / 6ll; }
constexpr int N = 1e5;
PST t(N);
int main() {
cin.tie(nullptr)->sync_with_stdio(false);
cout.tie(nullptr)->sync_with_stdio(false);
int tt = 1;
cin >> tt;
while (tt--) {
ll n;
cin >> n;
for (int i = 1; i <= idx; ++ i) {
t.tr[i] = {0, 0, 0, 0};
}
idx = 1;
vector<ll> a(n + 1);
vector<ll> sa(n + 1);
vector<ll> vec(0);
for (int i = 1; i <= n; ++ i) {
cin >> a[i];
vec.emplace_back(a[i]);
sa[i] = sa[i - 1] + a[i];
}
sort(vec.begin(), vec.end());
vec.erase(unique(vec.begin() + 1, vec.end()), vec.end());
auto find = [&](ll x) -> int {
return lower_bound(vec.begin(), vec.end(), x) - vec.begin() + 1;
};
int m = vec.size();
t.build(t.roots[0], 1, m);
for (int i = 1; i <= n; ++ i) {
int v = find(a[i]);
ll rv = vec[v - 1];
t.insert0(t.roots[i - 1], t.roots[i], 1, m, v, rv);
}
int q; cin >> q;
while (q--) {
ll l, r, k;
cin >> l >> r >> k;
int len = r - l + 1;
ll ans = f(len);
if (len == k) {
ans += sa[r] - sa[l - 1];
} else {
ans += t.querysum0(t.roots[l - 1], t.roots[r], 1, m, k);
}
cout << ans << "\n";
}
}
}
图论(graph)
二分图
int n, m, e;
std::cin >> n >> m >> e;
std::vector<std::vector<int>> g(n);
while (e--) {
int u, v;
std::cin >> u >> v;
u--, v--;
g[u].emplace_back(v);
}
std::vector<int> match(m, -1);
std::vector<bool> st(m, false);
auto find = [&](auto &&self, int u)->bool {
for (auto v : g[u]) if (!st[v]) {
st[v] = true;
if (match[v] == -1 || self(self, match[v])) {
match[v] = u;
return true;
}
}
return false;
};
int ans = 0;
for (int i = 0; i < n; ++i) {
st.assign(m, false);
ans += find(find, i);
}
std::cout << ans << '\n';
树上问题
最近公共祖先
int n, root, q, logn = 32;
vector<int> dep(n + 10); // 点的深度
vector<vector<int>> adj(n + 10, vector<int>(0)); // 图
vector<vector<int>> fa(n + 10, vector<int>(logn + 1)); // fa[u][i]表示从u点向上跳2^i层的祖先结点
dep[root] = 0;
//不同于树形DP,根节点还需要有一个超级原点,即0,故需要处理根节点和0
auto dfs = [&](auto self, int x, int father) -> void {
fa[x][0] = father;
dep[x] = dep[father] + 1;
for (int i = 1; i <= logn; ++ i) {
fa[x][i] = fa[ fa[x][i - 1] ][i - 1];
}
for (auto y : adj[x]) {
if (y == father) continue;
self(self, y, x);
}
};
dfs(dfs, root, 0);
auto lca = [&](int x, int y) {
if (dep[x] > dep[y]) swap(x, y);
for (int i = logn; i >= 0; -- i) {
if (dep[fa[y][i]] >= dep[x]) y = fa[y][i];
}
if (y == x) return x;
for (int i = logn; i >= 0; -- i) {
if (fa[y][i] != fa[x][i]) {
y = fa[y][i];
x = fa[x][i];
}
}
return fa[y][0];
};
树链剖分
重链剖分
class HLD { // Heavy-light Decomposition
public:
int n;
vector<int> top, fa, dep, siz, son, dfn, rnk;
vector<vector<int>> adj;
int cnt;
HLD() {}
HLD(int n) { init(n); }
void init(int n) {
this -> n = n;
top.resize(n + 1); // top[u] 存 u 所在重链的顶点
fa.resize(n + 1); // fa[u] 存 u 的父结点
dep.resize(n + 1); // dep[u] 存 u 的深度
siz.resize(n + 1); // siz[u] 存 u 的子树结点数
son.resize(n + 1); // son[u] 存 u 的重儿子
dfn.resize(n + 1); // dfn[u] 存 u 的 DFS 序,也是其在线段树中的编号
rnk.resize(n + 1); // rnk[u] 存 u 的 DFS 序对应的结点编号,有rnk[dfn[u]] = u
adj.resize(n + 1, {}); // 树
cnt = 0;
}
void addEdge(int u, int v) {
adj[u].emplace_back(v);
adj[v].emplace_back(u);
}
void build(int root = 1) {
top[root] = root;
dfs1(root, 0);
dfs2(root, root);
}
void dfs1(int u, int father) {
fa[u] = father;
dep[u] = dep[father] + 1;
siz[u] = 1;
for (auto &v : adj[u]) {
if (v == father) continue;
dfs1(v, u);
siz[u] += siz[v];
if (siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t;
dfn[u] = ++cnt;
rnk[cnt] = u;
if (!son[u]) return ;
dfs2(son[u], t);
for (auto &v : adj[u]) {
if (v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
int lca(int u, int v) { // 最近公共祖先
while (top[u] != top[v]) {
if (dep[top[u]] > dep[top[v]]) {
u = fa[top[u]];
} else {
v = fa[top[v]];
}
}
return dep[u] < dep[v] ? u : v;
}
int dist(int u, int v) { // 树上两点最短距离
return dep[u] + dep[v] - 2 * dep[lca(u, v)];
}
};
拓扑排序
有向图
vector<vector<int>> adj(n + 1, vector<int>());
vector<int> tp; // 拓扑序数组
vector<int> din(n + 1); // 入度,即指向该点的箭头数
auto toposort = [&]() {
queue<int> q;
for (int i = 1; i <= n; ++ i) {
if (din[i] == 0) q.push(i);
}
while (q.size()) {
int x = q.front();
q.pop();
tp.push_back(x);
for (auto y : adj[x]) {
din[y]--;
if (din[y] == 0) q.push(y);
}
}
return tp.size() == n;
};
无向图
int ans = 1;
int n;
cin >> n;
vector<vector<int>> adj(n + 2, vector<int>());
vector<int> tp; // 拓扑序数组
vector<int> din(n + 2); // 入度,即指向该点的箭头数
for (int i = 1; i <= n; ++ i) {
int l, r;
cin >> l >> r;
din[l] ++;
din[r + 1] ++;
adj[l].emplace_back(r + 1);
adj[r + 1].emplace_back(l);
}
auto toposort = [&](vector<vector<int>> &adj) {
queue<int> q;
vector<int> vis(n + 2);
for (int i = 1; i <= n + 1; ++ i) {
if (din[i] == 1) q.push(i);
}
while (q.size()) {
int x = q.front();
vis[x] = 1;
q.pop();
tp.push_back(x);
for (auto y : adj[x]) {
if (vis[y]) continue;
din[y] --;
if (din[y] == 1) q.push(y);
}
}
return tp.size() == n + 1;
};
if (toposort(adj)) {
ans = 1;
} else {
ans = 0;
}
cout << ans << "\n";
最短路
Dijkstra 算法
求解非负权图上单源最短路径的算法。
class edge {
public:
ll v, w;
};
struct node {
ll dis, u;
bool operator>(const node& a) const { return dis > a.dis; }
};
复杂度O(mlog(m))版本:
vector<vector<edge>> g(n + 1, vector<edge>(0));
vector<ll> pre(n + 1);
vector<int> path(n + 1);
auto dij = [&](int begin, int end) {
vector<ll> dis(n + 1, inf);
vector<ll> vis(n + 1);
priority_queue<node, vector<node>, greater<node>> q;
dis[begin] = 0;
q.push({0, begin});
while (!q.empty()) {
int u = q.top().u;
q.pop();
if (vis[u]) continue;
vis[u] = 1;
for (auto ed : g[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
pre[v] = u;
q.push({dis[v], v});
}
}
}
return dis[end];
};
auto dfs_path = [&](auto &self, int s, int t) -> void {
path[t] = 1;
if (t == s) {
return ;
} else {
self(self, s, pre[t]);
debug(t);
}
};
复杂度O(n^2)版本:
vector<vector<edge>> g(n + 1, vector<edge>(0));
auto dij = [&](int begin, int end) {
vector<ll> dis(n + 1, inf);
vector<ll> vis(n + 1);
dis[begin] = 0;
for (int i = 1; i <= n; ++ i) {
ll u = 0, mind = inf;
for (int j = 1; j <= n; ++ j) {
if (!vis[j] && dis[j] < mind) {
u = j;
mind = dis[j];
}
}
vis[u] = 1;
for (auto ed : g[u]) {
int v = ed.v, w = ed.w;
if (dis[v] > dis[u] + w) dis[v] = dis[u] + w;
}
}
return dis[end];
};
最小生成树(MST)
edge
class edge {
public:
ll u, v, w;
edge() {}
edge(ll u, ll v, ll w) : u(u), v(v), w(w) {}
bool operator<(const edge& a) const { return w < a.w; }
};
Kruskal算法
class DSU;
int main() {
int n, m;
cin >> n >> m;
vector<vector<edge>> adj(n + 1, vector<edge>(0));
vector<edge> g(m + 1);
DSU a(n);
for (int i = 1; i <= m; ++ i) {
ll u, v, w;
cin >> u >> v >> w;
g[i] = edge(u, v, w);
}
auto Kruskal = [&]() {
sort(g.begin() + 1, g.end());
ll cnt = 0, res = 0;
for (int i = 1; i <= m; ++ i) {
int xr = a.find(g[i].u), yr = a.find(g[i].v);
if (xr != yr) {
a.merge(xr, yr);
cnt ++;
res += g[i].w;
}
}
if (cnt == n) {
return res;
} else {
return -1ll;
}
};
Kruskal();
}
Prim算法
struct node {
ll u, dis;
node() {}
node(ll u, ll dis) : u(u), dis(dis) {}
bool operator<(const node& a) const { return dis > a.dis; }
};
int main() {
int n, m;
vector<vector<edge>> adj(n + 1, vector<edge>(0));
vector<ll> dis(n + 1);
vector<int> vis(n + 1, 0);
priority_queue<node> q;
auto addEdge = [&](ll u, ll v, ll w) {
adj[u].emplace_back(edge(u, v, w));
adj[v].emplace_back(edge(v, u, w));
};
auto Prim = [&](int root = 1) {
ll res = 0, cnt = 0;
for (int i = 1; i <= n; ++ i) dis[i] = inf;
dis[root] = 0;
q.push(node(root, 0));
while (!q.empty()) {
if (cnt >= n) break;
ll u = q.top().u, d = q.top().dis;
q.pop();
if (vis[u]) continue;
vis[u] = true;
cnt ++;
res += d;
for (auto ed : adj[u]) {
ll v = ed.v, w = ed.w;
if (w < dis[v]) {
dis[v] = w;
q.push({v, w});
}
}
}
if (cnt == n) {
return res;
} else {
return -1ll;
}
};
Prim(root);
}
计算几何
二维
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using DB = double;
const DB eps = 1e-9, pi = acos(-1), inf = 1e100;
int dcmp(DB x, DB y) { return fabs(x - y) < eps ? 0 : x > y ? 1 : -1; } // 比较大小
int sgn(DB d) { return fabs(d) < eps ? 0 : d > 0 ? 1 : -1; } // 判断正负
struct Point { // 定义点
DB x = 0, y = 0;
Point () {}
Point (DB x, DB y) : x(x), y(y) {}
Point operator+(const Point &P) const { return Point(x + P.x, y + P.y); }
Point operator-(const Point &P) const { return Point(x - P.x, y - P.y); }
Point operator*(DB p) const { return Point(x * p, y * p); }
Point operator/(DB p) const { return Point(x / p, y / p); }
DB operator&(const Point &P) const { return x * P.x + y * P.y; } // 点积 |A||B|cosθ
DB operator^(const Point &P) const { // 叉积 |A||B|sinθ
return x * P.y - y * P.x;
}
bool operator<(const Point &P) const {
return sgn(x - P.x) < 0 || (sgn(x - P.x) == 0 && sgn(y - P.y) < 0);
}
bool operator==(const Point &P) const { return !sgn(x - P.x) && !sgn(y - P.y); }
bool operator!=(const Point &P) const { return sgn(x - P.x) || sgn(y - P.y); }
friend istream &operator>>(istream &is, Point &rhs) {
return is >> rhs.x >> rhs.y;
}
friend ostream &operator<<(ostream &os, const Point &rhs) {
return os << '(' << rhs.x << ',' << rhs.y << ')';
}
};
using Vector = Point;
const Point O = {0, 0}; // 原点
// 向量A长度
DB Len(const Vector &A) { return sqrt(A & A); }
// 向量A长度的平方
DB Len2(const Vector &A) { return A & A; }
// 向量A,B夹角
DB Angle(const Vector &A, const Vector &B) { return acos((A & B) / Len(A) / Len(B)); }
// 两点间距离
DB Distance(const Point &A, const Point &B) { return Len(A - B); }
// ab在ac上的投影长度
DB Project(const Point &A, const Point &B, const Point &C) {
return (B - A & C - A) / Len(B - A);
}
// 向量A,B构成的平行四边形的有向面积
DB Area2(const Point &A, const Point &B, const Point &C) { return B - A ^ C - A; }
// 斜率
DB Slope(const Point &A, const Point &B) { return (A.y - B.y) / (A.x - B.x); }
// 向量A逆时针转动rad(弧度)
Vector Rotate(const Vector &A, DB rad) {
return Vector(A.x * cos(rad) - A.y * sin(rad), A.x * sin(rad) + A.y * cos(rad));
}
// 返回A的单位向量
Vector Norm(const Vector &P) { return P / Len(P); }
// 求凸包
vector<Point> Convex_hull(vector<Point> &p) {
sort(p.begin(), p.end());
p.erase(unique(p.begin(), p.end()), p.end());
int n = size(p);
vector<Point> ch;
// set<Point> st;
for (int i = 0; i < n; ++ i) {
while (size(ch) > 1 && sgn(Area2(ch.rbegin()[1], ch.rbegin()[0], p[i])) <= 0) {
// st.erase(prev(st.end()));
ch.pop_back();
}
ch.push_back(p[i]);
// st.insert(p[i]);
}
// st.erase(st.begin());
for (int i = n - 1, j = size(ch); i >= 0; -- i) {
// if (st.count(p[i])) continue;
while (size(ch) > 1 && sgn(Area2(ch.rbegin()[1], ch.rbegin()[0], p[i])) <= 0) {
ch.pop_back();
}
ch.push_back(p[i]);
}
if (size(ch) > 1) ch.pop_back();
return ch;
}
// 平面最近点对
DB Closest_pair(const vector<Point> &p, int l, int r) {
DB dist = inf;
if (l == r) return dist;
if (l + 1 == r) return Distance(p[l], p[r]);
int mid = l + r >> 1;
DB d1 = Closest_pair(p, l, mid), d2 = Closest_pair(p, mid + 1, r);
dist = min(d1, d2);
vector<Point> tmp;
for (int i = l; i <= r; ++ i)
if (fabs(p[mid].x - p[i].x) <= dist) tmp.push_back(p[i]);
for (int i = 0; i < tmp.size(); ++ i)
for (int j = i + 1; j < tmp.size(); ++ j) {
if (tmp[j].y - tmp[i].y >= dist) break;
dist = min(dist, Distance(tmp[i], tmp[j]));
}
return dist;
}
// 旋转卡壳,凸包直径
DB Rotating_calipers_point_pair_min(const vector<Point> &P) {
if (size(P) <= 2) return Distance(P[0], P[1]);
DB ans = 0;
for (int i = 0, j = 2, n = size(P); i < n; ++ i) {
auto a = P[i], b = P[(i + 1) % n];
while (dcmp(Area2(a, b, P[j]), Area2(a, b, P[(j + 1) % n])) < 0) j = (j + 1) % n;
ans = max({ans, Distance(a, P[j]), Distance(b, P[j])});
}
return ans;
}
// 旋转卡壳,返回最小矩形面积和矩形四点
DB Rotaring_calipers_area_min(const vector<Point> &p, array<Point, 4> &ans) {
int n = size(p);
DB min_area = inf;
for (int i = 0, a = 2, b = 1, c = 2; i < n; ++ i) {
auto d = p[i], e = p[(i + 1) % n];
while (dcmp(Area2(d, e, p[a]), Area2(d, e, p[(a + 1) % n])) < 0) a = (a + 1) % n;
while (dcmp(Project(d, e, p[b]), Project(d, e, p[(b + 1) % n])) < 0) b = (b + 1) % n;
if (i == 0) c = a;
while (dcmp(Project(d, e, p[c]), Project(d, e, p[(c + 1) % n])) > 0) c = (c + 1) % n;
auto x = p[a], y = p[b], z = p[c];
auto h = Area2(d, e, x) / Len(e - d);
auto w = ((y - z) & (e - d)) / Len(e - d);
if (h * w < min_area) {
min_area = h * w;
ans[0] = d + Norm(e - d) * Project(d, e, y);
ans[3] = d + Norm(e - d) * Project(d, e, z);
auto u = Norm(Rotate(e - d, pi / 2));
ans[1] = ans[0] + u * h;
ans[2] = ans[3] + u * h;
}
}
return min_area;
}
struct Line { // 定义直线
Point p1, p2;
Line() {}
Line(const Point &p1, const Point &p2) : p1(p1), p2(p2) {}
Line (const Point &p, DB angle) { // 根据点和倾斜角angle确定直线,0 <= angle <= pi
p1 = p;
if (sgn(angle - pi / 2) == 0) p2 = p1 + Point(0, 1);
else p2 = p1 + Point(1, tan(angle));
}
Line(DB a, DB b, DB c) { // ax + by + c = 0
if (sgn(a) == 0) p1 = Point(0, -c / b), p2 = Point(1, -c / b);
else if (sgn(b) == 0) p1 = Point(-c / a, 0), p2 = Point(-c / a, 1);
else p1 = Point(0, -c / b), p2 = Point(1, (-c - a) / b);
}
};
using Segment = Line;
const Line Ox = {O, {1, 0}}, Oy = {O, {1, 0}};
// 点和线的位置关系
int Point_line_relation(const Point &p, const Line &v) {
int c = sgn(p - v.p1 ^ v.p2 - v.p1);
return c == 0 ? 0 : c < 0 ? 1 : 2; // 0:p在v上,1:p在v左侧,2:p在v右侧
}
// 点到直线的距离
DB Dis_point_line(const Point &p, const Line &v) {
return fabs(p - v.p1 ^ v.p2 - v.p1) / Distance(v.p1, v.p2);
}
// 点到线段的距离
DB Dis_point_seg(const Point &p, const Segment &v) {
if (sgn(p - v.p1 & v.p2 - v.p1) < 0 || sgn(p - v.p2 & v.p1 - v.p2) < 0) {
return min(Distance(p, v.p1), Distance(p, v.p2));
}
// 点的投影在线段上
return Dis_point_line(p, v);
}
// 返回线段上的某一点
Point Point_on_seg(const Point &A, const Point &B, DB d) {
return A + (B - A) * d / Distance(A, B);
}
// 判断点是否在线段上
bool Point_on_seg(const Point &p, const Segment &v) {
return !sgn(p - v.p1 ^ v.p2 - v.p1) && sgn(p - v.p1 & p - v.p2) <= 0;
}
// 判断线段ab和cd是否相交(包括端点,去掉等于即不包括端点)
bool Corss_segment(const Point &a, const Point &b, const Point &c, const Point &d) {
DB c1 = b - a ^ c - a, c2 = b - a ^ d - a;
DB d1 = d - c ^ a - c, d2 = d - c ^ b - c;
return sgn(c1) * sgn(c2) <= 0 && sgn(d1) * sgn(d2) <= 0; // 1相交,0,不相交
}
int Line_relation(const Line &v1, const Line &v2) { // 两条直线的位置关系
if (sgn(v1.p2 - v1.p1 ^ v2.p2 - v2.p1) == 0) {
if (Point_line_relation(v1.p1, v2) == 0) return 1; // 重合
return 0; // 平行
}
return 2; // 相交
}
// 直线与线段是否相交
bool Line_Segment_relation(const Line &v1, const Segment &v2) {
// return sgn(Cross(v1.p2 - v1.p1, v2.p1 - v1.p1)
* Cross(v1.p2 - v1.p1, v2.p2 - v1.p1)) <= 0;
return sgn(Area2(v1.p1, v1.p2, v2.p1) * Area2(v1.p1, v1.p2, v2.p2)) <= 0;
}
// 两条直线的交点,线段1:AB,线段2:CD
// 使用前保证直线AB,CD不共线且不平行
Point Cross_point(const Point &A, const Point &B, const Point &C, const Point &D) {
DB s1 = B - A ^ C - A, s2 = B - A ^ D - A;
return Point(C.x * s2 - D.x * s1, C.y * s2 - D.y * s1) / (s2 - s1);
}
// 点在直线上的投影
Point Point_line_proj(const Point &p, const Line &v) {
DB k = (v.p2 - v.p1 & p - v.p1) / Len2(v.p2 - v.p1);
return v.p1 + (v.p2 - v.p1) * k;
}
// 点关于直线的对称点
Point Point_line_symmetry(const Point &p, const Line &v) {
Point q = Point_line_proj(p, v);
return Point(2 * q.x - p.x, 2 * q.y - p.y);
}
// 求多边形面积
DB Polygon_area(const vector<Point> &p) {
DB area = 0;
for (int i = 0, n = size(p); i < n; ++ i)
area += p[i] ^ p[(i + 1) % n];
return area / 2;
}
// 判断点跟多边形的位置关系
int Point_in_polygon(Point &p, vector<Point> &poly) {
for (auto &x : poly)
if (x == p) return 3; // 点在多边形的顶点上
int n = poly.size();
for (int i = 0; i < n; ++ i) // 点在多边形的边上
if (Point_on_seg(p, Line(poly[i], poly[(i + 1) % n]))) return 2;
int num = 0;
for (int i = 0; i < n; ++ i) {
int c = sgn((p - poly[i]) ^ (p - poly[(i + 1) % n]));
int u = sgn(poly[i].y - p.y), v = sgn(poly[(i + 1) % n].y - p.y);
if (c > 0 && u < 0 && v >= 0) num ++ ;
if (c < 0 && u >= 0 && v < 0) num -- ;
}
return num != 0; // 1:点在外部,0:点在内部
}
Point Polygon_center(const vector<Point> &p) { // 返回多边形的重心
int n = p.size();
Point ans = Point(0, 0);
if (Polygon_area(p) == 0) return ans ;
for (int i = 0; i < n; ++ i)
ans = ans + (p[i] + p[(i + 1) % n]) * (p[i] ^ p[(i + 1) % n]);
return ans / Polygon_area(p) / 6;
}
// 多边形上的格点个数
int Grid_onedge(const vector<Point> &p) {
int cnt = 0;
for (int i = 0, n = size(p); i < n; ++ i)
cnt += gcd((int)abs(p[i].x - p[(i + 1) % n].x), (int)abs(p[i].x - p[(i + 1) % n].y));
return cnt;
}
int Gird_inside(const vector<Point> &p) {
int cnt = 0;
for (int i = 0, n = size(p); i < n; ++ i)
cnt += p[(i + 1) % n].y * (p[i].x - p[(i + 2) % n].x);
return (abs(cnt) - Grid_onedge(p)) / 2 + 1;
}
/*
struct Line { // 有向直线,它的左边就是对应的半平面
Point p; // 直线上任意一点
Vector v; // 方向向量,左边就是对应的半平面
DB deg; // 极角,从x正半轴旋转到v的角度
Line (const Point &p, const Vector &v) : p(p), v(v) { deg = atan2(v.y, v.x); }
bool operator<(const Line &L) { return deg < L.deg; } // 极角排序
};
using Segment = Line;
// 点是否在直线上(y = kx + b)
bool Point_line_relation(const Point &p, const Line &L) {
DB y = L.p.y + (p.x - L.p.x) * L.v.y / L.v.x;
return dcmp(y, p.y) == 0;
}
// 点p在线L左边,即点p在线L外面
bool OnLeft(const Line &L, const Point &p) { return sgn(L.v ^ (p - L.p)) < 0; }
Point Cross_point(const Line &a, const Line &b) { // 两直线交点(点线式)
double t = (b.v ^ (a.p - b.p)) / (a.v ^ b.v);
return a.p + a.v * t;
}
vector<Point> half_plane_intersection(vector<Line> &L) {// 求半平面交,返回凸多边形
sort(L.begin(), L.end()); // 极角排序
int n = size(L), hh = 0, tt = 0;
vector<Point> p(n);
vector<Line> q(n);
q[0] = L[0];
for (int i = 1; i < n; ++ i) {
while (hh < tt && !OnLeft(L[i], p[tt - 1])) tt -- ; // 删除尾部半平面
while (hh < tt && !OnLeft(L[i], p[hh])) hh ++ ; // 删除首部半平面
q[ ++ tt] = L[i];
if (sgn(q[tt].v ^ q[tt - 1].v) == 0) { // 极角相同的两个半平面,保留左边
tt -- ;
if (OnLeft(q[tt], L[i].p)) q[tt] = L[i];
}
if (hh < tt) p[tt - 1] = Cross_point(q[tt - 1], q[tt]); // 计算队尾半平面交点
}
while (hh < tt && !OnLeft(q[hh], p[tt - 1])) tt -- ;
if (tt - hh <= 1) return {};
p[tt] = Cross_point(q[tt], q[hh]); // 计算队尾半平面交点
return vector<Point>(p.begin() + hh, p.begin() + tt + 1);
}
*/
struct Circle { // 定义圆
Point c;
DB r;
Circle() {}
Circle(const Point &c, DB r = 0) : c(c), r(r) {}
Point Oxy(DB a) { // 通过圆心角求坐标
return Point(c.x + cos(a) * r, c.y + sin(a) * r);
}
};
int Point_circle_relation(const Point &p, const Circle &C) { // 点与圆的关系
DB dist = Distance(p, C.c);
if (sgn(dist - C.r) < 0) return 0; // 点在圆内
if (sgn(dist - C.r) == 0) return 1; // 点在圆上
return 2; // 点在圆外
}
int Line_circle_relation(const Line v, const Circle &C) { // 直线和圆的关系
DB dist = Dis_point_line(C.c, v);
if (sgn(dist - C.r) < 0) return 0; // 直线和圆相交
if (sgn(dist - C.r) == 0) return 1; // 直线和圆相切
return 2; // 直线在圆外
}
int Seg_circle_relation(const Segment &v, const Circle &C) { //线段和圆的关系
DB dist = Dis_point_seg(C.c, v);
if (sgn(dist - C.r) < 0) return 0; // 线段在圆内
if (sgn(dist - C.r) == 0) return 1; // 线段与圆相切
return 2; // 线段在圆外
}
int Circle_circle_relation(const Circle &c1, const Circle &c2) { // 圆和圆的关系
DB dist = Distance(c1.c, c2.c);
if (sgn(dist) == 0) {
if (c1.r == c2.r) return -1; // 两圆重合
return 0; // 两圆圆心相同
}
if (dcmp(dist, c1.r + c2.r) == 0) return 1; // 两圆相切
if (dcmp(dist, c1.r + c2.r) < 0) return 2; // 两圆相交
return 3; //两圆相离
}
Point Dot_circle(const Point &p, const Circle &C) { // 计算圆上到点p的最近点
Point u, v, c = C.c;
DB dist = Distance(c, p), r = C.r;
if (sgn(dist)) return p;
u.x = c.x + r * fabs(c.x - p.x) / dist;
u.y = c.y + r * fabs(c.y - p.y) / dist * sgn((c.x - p.x) * (c.y - p.y));
v.x = c.x - r * fabs(c.x - p.x) / dist;
v.y = c.y - r * fabs(c.y - p.y) / dist * sgn((c.x - p.x) * (c.y - p.y));
return Distance(u, p) < Distance(v, p) ? u : v;
}
// 返回直线与圆的交点(线段的话判断点是否在线段上即可)
vector<Point> Line_cross_circle(const Line &v, const Circle &C) {
if (Line_circle_relation(v, C) == 2) return {};
Point q = Point_line_proj(C.c, v); // 圆心在直线上的投影
DB d = Dis_point_line(C.c, v), k = hypot(C.r, d), len = sqrt(C.r * C.r - d * d); // 圆心到直线的距离
if (sgn(k) == 0) return {q};
// if (!Point_on_segment(q, v)) {
// DB mind = min(Distance(C.c, v.p1), Distance(C.c, v.p2));
// if(dcmp(C.r, mind) <= 0) return {};
// }
return {q + Norm(v.p1 - v.p2) * len, q + Norm(v.p2 - v.p1) * len};
}
Point Circle_center(const Point &A, const Point &B, const Point &C) { //返回三角形垂心(外接圆圆心)
Vector AB = B - A, AC = C - A;
DB lenb = (AB & AB) / 2, lenc = (AC & AC) / 2, d = AB & AC;
return A + Point(lenb * AC.y - lenc * AB.y, lenc * AB.x - lenb * AC.x) / d;
}
// 返回三角形内接圆
Circle Circle_center_incircle(const Point &p1, const Point &p2, const Point &p3) {
DB a = Len(p2 - p3), b = Len(p3 - p1), c = Len(p1 - p2);
Point p = (p1 * a + p2 * b + p3 * c) / (a + b + c);
return Circle(p, Dis_point_line(p, Line(p1, p2)));
}
Circle Min_cover_circle(vector<Point> &p) {
random_shuffle(p.begin(), p.end());
Point c = p[0];
DB r = 0.0;
for (int i = 1; i < size(p); ++ i) {
if (sgn(Distance(p[i], c) - r) > 0) {
c = p[i], r = 0.0;
for (int j = 0; j < i; ++ j) {
if (sgn(Distance(p[j], c) - r) > 0) {
c = (p[i] + p[j]) / 2;
r = Distance(p[j], c);
for (int k = 0; k < j; ++ k) {
if (sgn(Distance(p[k], c) - r) > 0) {
c = Circle_center(p[i], p[j], p[k]);
r = Distance(p[i], c);
}
}
}
}
}
}
return Circle(c, r);
}
// 返回两圆交点
vector<Point> Circle_circle_intersection(Circle &c1, Circle &c2) {
DB d = Len(c1.c - c2.c);
if (sgn(d) == 0) return {}; // 可能出现两圆重合需特判
if (sgn(c1.r + c2.r - d) < 0 || sgn(fabs(c1.r - c2.r) - d) > 0) return {}; //相离或包含
Point c = c2.c - c1.c;
DB a = atan2(c.y, c.x);
DB da = acos((c1.r * c1.r + d * d - c2.r * c2.r) / (2 * c1.r * d));
Point p1 = c1.Oxy(a - da), p2 = c1.Oxy(a + da);
if (p1 == p2) return vector<Point>{p1};
return vector<Point>{p1, p2};
}
// 点到圆的切线
vector<Point> Point_circle_tangents(const Point &p, const Circle &C) {
Vector u = C.c - p;
DB dist = Len(u);
if (dist < C.r) return {};
else if (sgn(dist - C.r) == 0) {
return vector<Point>{Rotate(u, pi / 2)};
} else {
DB ang = asin(C.r / dist);
return vector<Point>{Rotate(u, -ang), Rotate(u, ang)};
}
}
// 两圆的公切线
int Circle_circle_tangents(Circle &A, Circle &B, vector<Point> &a, vector<Point> &b) {
if (A.r < B.r) swap(A, B), swap(a, b);
DB d2 = Len2(A.c - B.c), rdiff = A.r - B.r, rsum = A.r + B.r;
if (dcmp(d2, rdiff + rsum) < 0) return 0; // 内含
DB base = atan2(B.c.y - A.c.y, B.c.x - A.c.x);
if (d2 == 0 && A.r == B.r) return -1; // 无限多条切线
if (dcmp(d2, rdiff * rdiff) == 0) {
a.push_back(A.Oxy(base)), b.push_back(B.Oxy(base));
return 1;
}
DB ang = acos(rdiff / sqrt(d2));
a.push_back(A.Oxy(base + ang)), b.push_back(B.Oxy(base + ang));
a.push_back(A.Oxy(base - ang)), b.push_back(B.Oxy(base - ang));
if (dcmp(d2, rsum * rsum) == 0) {
a.push_back(A.Oxy(base)), b.push_back(B.Oxy(pi + base));
} else if (dcmp(d2, rsum * rsum) > 0) {
DB ang = acos((A.r + B.r) / sqrt(d2));
a.push_back(A.Oxy(base + ang)), b.push_back(B.Oxy(pi + base + ang));
a.push_back(A.Oxy(base - ang)), b.push_back(B.Oxy(pi + base - ang));
}
return size(a);
}
//两圆相交面积
DB Circle_circle_Area(const Circle &c1, const Circle &c2) {
DB d = Len(c1.c - c2.c);
if (dcmp(c1.r + c2.r, d) <= 0) return 0;
if (dcmp(d, fabs(c1.r - c2.r)) <= 0) return pi * min(c1.r, c2.r) * min(c1.r, c2.r);
DB x = (d * d + c1.r * c1.r - c2.r * c2.r) / (2 * d);
DB p = (c1.r + c2.r + d) / 2;
DB t1 = acos(x / c1.r), t2 = acos((d - x) / c2.r);
DB s1 = c1.r * c1.r * t1, s2 = c2.r * c2.r * t2, s3 = 2 * sqrt(p * (p - c1.r) * (p - c2.r) * (p - d));
return s1 + s2 - s3;
}
// 返回扇形面积
DB Sector_area(const Circle &C, const Point &a, const Point &b) {
DB angle = Angle(a - C.c, b - C.c);
if (sgn(a ^ b) < 0) angle = -angle;
return C.r * C.r * angle / 2;
}
// 圆和三角形相交面积
DB Circle_triangle_area(const Circle &C, const Point &a, const Point &b) {
auto da = Distance(C.c, a), db = Distance(C.c, b);
if (dcmp(C.r, da) >= 0 && dcmp(C.r, db) >= 0) return (a ^ b) / 2;
if (!sgn(a ^ b)) return 0;
auto p = Line_cross_circle(Line(a, b), C);
if (size(p) == 0) return Sector_area(C, a, b);
if (dcmp(C.r, db) >= 0) return (p[0] ^ b) / 2 + Sector_area(C, a, p[0]);
if (dcmp(C.r, da) >= 0) return (a ^ p[1]) / 2 + Sector_area(C, p[1], b);
return Sector_area(C, a, p[0]) + (p[0] ^ p[1]) / 2 + Sector_area(C, p[1], b);
}
struct Matrix {
Point p1, p2;
Matrix() {}
Matrix(const Point &p1, const Point &p2) : p1(p1), p2(p2) {}
};
// 扫描线求矩形面积并
DB Atlantis(const vector<Matrix> &mt) {
vector<DB> ver;
int n = size(mt);
for (int i = 0; i < n; ++ i) {
ver.push_back(mt[i].p1.x);
ver.push_back(mt[i].p2.x);
}
sort(ver.begin(), ver.end());
ver.erase(unique(ver.begin(), ver.end()), ver.end());
DB area = 0;
for (int i = 1; i < size(ver); ++ i) {
int x1 = ver[i - 1], x2 = ver[i];
vector<pair<DB, DB>> strip;
for (int j = 0; j < n; ++ j) {
if (mt[j].p1.x <= x1 && mt[j].p2.x >= x2) {
strip.push_back({mt[j].p1.y, mt[j].p2.y});
}
}
sort(strip.begin(), strip.end());
DB len = 0;
for (int j = 0, k = -1e9; j < size(strip); ++ j) {
if (strip[j].second >= k) {
len += strip[j].second - max((DB)k, strip[j].first);
k = strip[j].second;
}
}
area += len * (x2 - x1);
}
return area;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
cin>>n;
std::vector<Point> a(n);
for (int i = 0; i < n; ++i) {
std::cin >> a[i];
}
for (int i = 0; i < n; ++i) {
std::cout << a[i] << " \n"[i == n - 1];
}
}
三维
#include <bits/stdc++.h>
using namespace std;
using DB = double;
const DB eps = 1e-12, inf = 1e100, pi = acos(-1);
DB dcmp(DB x, DB y) { return fabs(x - y) < eps ? 0 : x < y ? -1 : 1; }
DB sgn(DB x) { return fabs(x) < 0 ? 0 : x < 0 ? -1 : 1; }
DB rand_eps() { return ((DB)rand() / RAND_MAX - 0.5) * eps; }
struct Point3 {
DB x, y, z;
Point3 () {}
Point3 (DB x, DB y, DB z) : x(x), y(y), z(z) {}
void shake() { x += rand_eps(), y += rand_eps(), z += rand_eps(); }
Point3 operator+(const Point3 &P) const {
return Point3(x + P.x, y + P.y, z + P.z);
}
Point3 operator-(const Point3 &P) const {
return Point3(x - P.x, y - P.y, z - P.z);
}
Point3 operator*(DB p) const { return Point3(x * p, y * p, z * p); }
Point3 operator/(DB p) const { return Point3(x / p, y / p, z / p); }
DB operator&(const Point3 &P) const { return x * P.x + y * P.y + z * P.z; }
Point3 operator^(const Point3 &P) const {
return Point3(y * P.z - z - P.y, z * P.x - x * P.z, x * P.y - y * P.x);
}
friend istream &operator>>(istream &is, Point3 &rhs) {
return is >> rhs.x >> rhs.y >> rhs.z;
}
friend ostream &operator<<(ostream &os, const Point3 &rhs) {
return os << '(' << rhs.x << ',' << rhs.y << ',' << rhs.z << ')';
}
};
using Vector3 = Point3;
bool cmp(const Point3 &a, const Point3 &b) {
if (a.x == b.x) {
if (a.y == b.y) { return a.z < b.z; }
else { return a.y < b.y; }
} else { return a.x < b.x; }
}
// 最近点对
DB Closest_pair(const vector<Point3> &p, int l, int r) {
DB dist = inf;
if (l == r) return dist;
if (l + 1 == r) return Distance(p[l], p[r]);
int mid = l + r >> 1;
DB d1 = Closest_pair(p, l, mid), d2 = Closest_pair(p, mid + 1, r);
dist = min(d1, d2);
vector<Point3> tmp;
for (int i = l; i <= r; ++ i)
if (fabs(p[mid].x - p[i].x) <= dist) tmp.push_back(p[i]);
for (int i = 0; i < tmp.size(); ++ i)
for (int j = i + 1; j < tmp.size(); ++ j) {
dist = min(dist, Distance(tmp[i], tmp[j]));
}
return dist;
}
DB Len(const Vector3 &A) { return sqrt(A & A); }
DB Len2(const Vector3 &A) { return A & A; }
DB Distance(const Vector3 &A, const Vector3 &B) { return Len(A - B); }
// 三角形面积的两倍
DB Area2(const Point3 &A, const Point3 &B, const Point3 &C) { return Len(B - A ^ C - A); }
DB Angle(const Vector3 &A, const Vector3 &B) { return acos((A & A) / Len(A) / Len(B)); }
// 判断点是否在三角形中
bool Point_in_triangle(const Point3 &A, const Point3 &B, const Point3 &C, const Point3 p) {
return dcmp(Area2(p, A, B) + Area2(p, A, C) + Area2(p, B, C), Area2(A, B, C)) == 0;
}
// 四面体有向面积*6
DB volume4(const Point3 &A, const Point3 &B, const Point3 &C, const Point3 &D) {
return ((B - A) ^ (C - A)) & (D - A);
}
// 四面体的重心
Point3 Centroid(const Point3 &A, const Point3 &B, const Point3 &C, const Point3 &D) {
return (A + B + C + D) / 4.0;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号