P2184 贪婪大陆

Luogu 题目传送门

洛谷打完卡(运势 § 小吉 § ) 后，打算做一道线段树的题，ranho并来到了这道题。

\(\;\)

题目大意

小 FF 在一条长度为 \(N\) 的战壕上布置防御，面对蚂蚁进攻。他有无数种地雷，每次操作让 SCV 在区间 [\(L\), \(R\)] 内埋放一种新型地雷（不同于已埋的）。有时，他会查询区间 [\(L'\), \(R'\)] 内不同地雷种类的数量。我们需要回答每个查询该区间内独特地雷类型的总数。

输入样例：

5 4
1 1 3
2 2 5
1 2 4
2 3 5

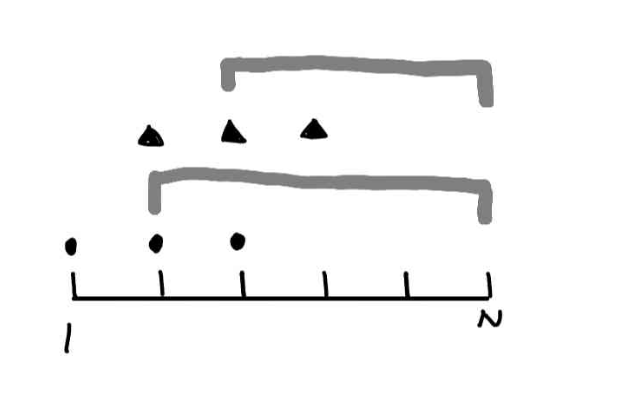
每一个图形是一种地雷

输出为:

1
2

\(\;\)

算法!

这里可以选择用线段树，或者选择树状数组。
树状数组有点难理解，所以我选择了线段树

Part 1 (Update 函数)

在这个更新函数，我用了差分数组来处理地雷的放置操作。对于每次放置一种新型地雷于区间 [L, R]，我们在起始位置 L 的起始树 tree_start 中增加 1，并在结束位置 R 的结束树 tree_end 中增加 1。这样我们无需直接修改整个区间。
更新函数遵循经典的线段树单点更新模板：

• 当递归到达叶子节点（即 \(l\) == \(r\) 时）时，对该节点的值增加 1
• 否则，根据目标位置 \(ql\) 递归至左子树或右子树

并在返回时通过 pushup 函数合并子节点信息。

Part 2 (Query 函数)

我的查询函数也是一个经典线段树的查询模板:
查询起始树中从 1 到 \(R'\) 的前缀和，减去结束树中从 1 到 \(L'-1\) 的前缀和 (若 \(L'\) 为 1，则后者为 0)。

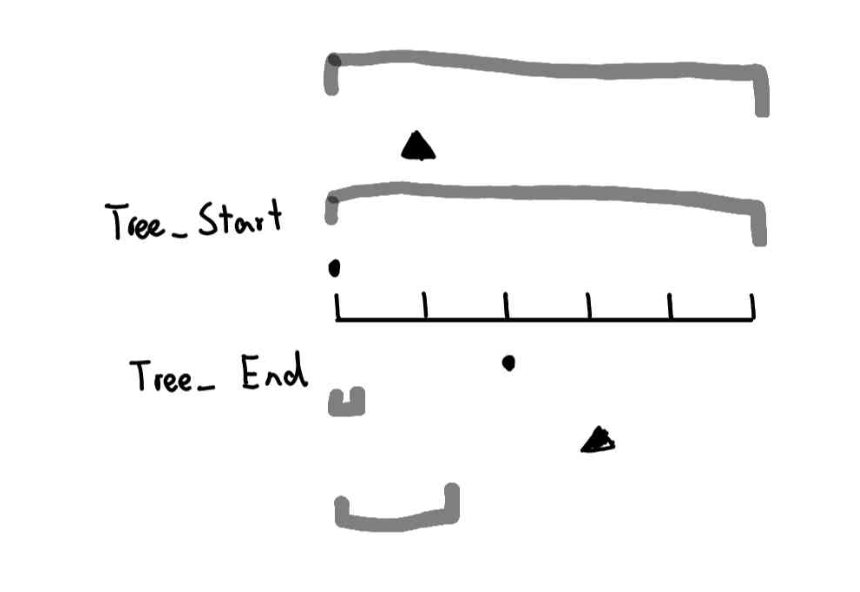
上面的图是对于测试数据。我们可以看到第一次查询的时候，我们会查询 \(tree\_start\) 从\(1 \sim 5\) 的地雷数量 (1)，再查询 \(tree\_end\) 从 \(1 \sim 1\) 的地雷数量 (0)。
他们的差就是区间地雷的"品牌" (1-0=0)。
第二次查询的时候：
查询 tree_start 从 \(1 \sim 5\) 的地雷数量 (2)。
查询 tree_end 从 \(1 \sim 2\) 的地雷数量 (0)
差: 2-0=2 就是答案

\(\;\)

时间复杂度：O(M log N)

废话不多说，代码直接上

完整代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define pa pair<int,int>
const int maxn=1e5;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0' && ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;}

int n,m,l,r,op;
int tree_start[maxn<<2],tree_end[maxn<<2];
void pushup(int rt,int tree[]) {tree[rt]=tree[rt<<1]+tree[rt<<1|1];}
void update(int l,int r,int rt,int ql,int tree[]) {
    if (l==r) return tree[rt]+=1,void();
    int mid=(l+r)>>1;
    if (ql<=mid) update(l,mid,rt<<1,ql,tree);
    else update(mid+1,r,rt<<1|1,ql,tree);
    pushup(rt,tree);
    return void();
}
int query(int l,int r,int rt,int ql,int qr,int tree[]) {
    if (ql<=l && qr>=r) return tree[rt];
    int mid=(l+r)>>1, tmp=0;
    if (ql<=mid) tmp+=query(l,mid,rt<<1,ql,qr,tree);
    if (mid<qr) tmp+=query(mid+1,r,rt<<1|1,ql,qr,tree);
    return tmp;
}

signed main(){
    n=read();m=read();
    memset(tree_start,0,sizeof(tree_start));
    memset(tree_end,0,sizeof(tree_end));
    for(int i=1;i<=m;i++) {
        op=read(); l=read(); r=read();
        if (op==1){
            update(1,n,1,l,tree_start);
            update(1,n,1,r,tree_end);
        }
        else
            cout<<query(1,n,1,1,r,tree_start)-(l==1?0:query(1,n,1,1,l-1,tree_end))<<endl;
    }
    return 0;
}

警示后人

1. 每一次放的地雷品牌都不一样
2. 同一个位置可以放多个地雷
3. Tree的大小要 maxn<<2 (=maxn*4)