2021寒假ACM集训队第一次训练-搜索(一)
A-小宋银行的贷款漏洞

PZ's solution
1.贷款利率\(\frac{a_1}{t}\)是不变的,例如\(x=100\quad t=2\),则贷款利率为\(\frac{1}{2}\),最终连本带息须还的金额为\(100*(1+\frac{1}{2})^2=225\),所以得到\(ans=x*(1+\frac{a_1}{t})^t\);
2.对于\(t=ZERO\)的情况,会发现没有贷款利率,直接得到\(ans=x\);
3.对于\(t=+INF\)的情况,在《高等数学上册》,有一重要极限:
对于本题,当\(t\)趋近于无限时,可以发现最终答案为
应用重要极限,得到:
则可以得到\(ans=x*e^{a_1}\)
ps.本题对\(e\)的精度有要求,代码中为最低精度,且答案向下取整;
- TAG:数学
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
using namespace std;
#define e (double)2.71828182845904
string x,t;
long long T,res,a1;
double ans,new_ans;
int main(){
scanf("%lld",&T);
for(int j=1;j<=T;++j){
res=ans=0;
cin>>x>>t;
a1=x[0]-'0';
for(int i=0;i<x.size();++i)
ans=ans*10+x[i]-'0';
new_ans=1;
if('0'<=t[0]&&t[0]<='9'){
for(int i=0;i<t.size();++i)
res=res*10+t[i]-'0';
for(int i=1;i<=res;++i)
new_ans*=(1+a1*1.0/res*1.0);
ans=ans*new_ans;
cout<<"#Case "<<j<<" : "<<(long long)(ans)<<endl;
} else if(t=="ZERO"){
cout<<"#Case "<<j<<" : "<<x<<endl;
} else if(t=="+INF"){
for(long long i=1;i<=a1;++i)
new_ans*=e;
ans=ans*new_ans;
cout<<"#Case "<<j<<" : "<<(long long)(ans)<<endl;
}
}
return 0;
}
B-三明治

Solution
思路借鉴于skylee的[JOISC2016]サンドイッチ
1.通过观察,可以发现,只有如图的四角的三明治才有机会再开始时被吃掉;
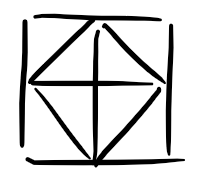
2.且经过简单分析,可以得出,当一个大三明治中的一个小三明治被吃时,另一个也同时被吃掉一定使答案最优;
3.但通过思考发现,如果从四角开始搜索,尝试吃三明治,会发现两个问题:
1).如何防止不会吃到原先吃过的三明治;
2).如何防止不会因为走被吃过三明治的道路导致现在答案过小,或是没有按照最优道路吃三明治而导致当前答案过大;
4.可以发现,从四角搜索具有局限性,所以转换思维,考虑从每个大三明治向四周去吃(时间限制为5s,可以提醒时间复杂度可以宽松考虑);
5.观察样例和进行分析,可以发现,三明治一定会先一直往一个方向吃,直到不能吃当前方向的三明治才开始考虑换方向吃;
抽象来说,即为吃三明治的路径具有某种单调性,且因为枚举每个被吃的位置,所以可以实现得出最优解;
1).如当前三明治切法为\(N\),那么如果其为从左侧吃到当前三明治,则其来的方向只能为左和下;
2).如当前三明治切法为\(N\),那么如果其为从右侧吃到当前三明治,则其来的方向只能为右和上;
3).如当前三明治切法为\(Z\),那么如果其为从左侧吃到当前三明治,则其来的方向只能为左和上;
4).如当前三明治切法为\(Z\),那么如果其为从右侧吃到当前三明治,则其来的方向只能为右和上;
5).通过这种性质,可以使当前吃法借助前面的吃法,直接从前面的吃法铺路过来吃,进行答案的累加;
6.具体方法上,可以枚举每个大三明治位置,且因为有四角作为起始和单调性质的缘故,需要正序和倒序遍历两遍;
7.在搜索时,我们强制判断能吃其相应来的地方,判断其是否能吃到合法边界;
1).如果相邻的位置被吃掉,则相邻位置对应的来的方向的边界上的三明治也要被吃;
2).此时,如果吃不到边界,或者出现吃成闭环(需要吃已经被吃的三明治)时,说明这个位置永远都不能被吃到;
8.如图代表代码中的当前大三角形方向,具体细节见代码;
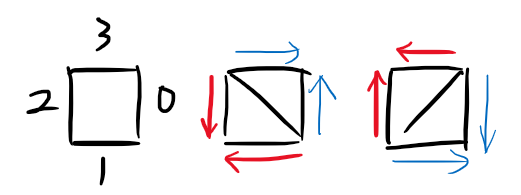
- TAG:搜索;剪枝
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<climits>
using namespace std;
#define N 405
char mp[N][N];
int n,m,res,flag,ans[N][N],vis[N][N];
int fx[]={0,-1,0,1};
int fy[]={-1,0,1,0};
bool check(int x,int y){ return 1<=x&&x<=n&&1<=y&&y<=m; }
void dfs(int x,int y,int d){
if(vis[x][y]==-1){ flag=1; return; }
//当vis[x][y]==-1时,说明当前三明治被吃过,且是必须要再被吃才能往后吃的
//这样的吃法当然是不合法的,使用flag作为标志,来表示当前三明治怎样都不能被吃到
if(vis[x][y]==1) return;
//当vis[x][y]==1时,说明当前三明治被吃过,但原来的三明治是不必须依靠吃它才能往后吃,这只是一条原先就可以被扩散到的吃法
res+=2;//一次直接将两个小三明治全吃掉
vis[x][y]=-1;
//在开始吃必须吃的三明治前,给vis[x][y]置-1
int p=((mp[x][y]=='N') ? 3 : 1);
if(check(x-fx[d],y-fy[d])) dfs(x-fx[d],y-fy[d],d);
if(check(x-fx[d^p],y-fy[d^p])) dfs(x-fx[d^p],y-fy[d^p],d^p);
//正序时,如当前大三明治切法为N,则
//要吃左和下,当前对应p为3
//d^p=2^3=1
//正序时,如当前大三明治切法为Z,则
//要吃左和上,当前对应p为1
//d^p=2^1=3
//倒序时,如当前大三明治切法为N,则
//要吃右和上,当前对应p为3
//d^p=0^3=3
//倒序时,如当前大三明治切法为Z,则
//要吃右和下,当前对应p为1
//d^p=0^1=1
vis[x][y]=1;
//吃完必须吃的三明治后,说明这是一条合法的吃法路线
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
cin>>mp[i][j];
for(int i=1;i<=n;++i){
flag=res=0;
//关于单调性,可以通过res=0和循环中res不置零看出,具体来说,就是
//如果flag没有置1,说明前面的大三明治都能被吃掉,且有一个res值代表吃掉前面大三明治的一种合法结果
//那么,当前的大三明治一但搜寻到vis[x][y]==1的位置,就说明可以接到前面大三明治的一种吃法,这样就不需要再搜索,累加res的值了
//且当前res值原本就是吃掉前面大三明治的结果加上当前大三明治吃到前面大三明治的结果的和
memset(vis,0,sizeof(vis));
for(int j=1;j<=m;++j){
if(!flag) dfs(i,j,2);
ans[i][j]=flag?INT_MAX:res;
}
flag=res=0;
memset(vis,0,sizeof(vis));
//再倒序一边,因为来的方向不一样,可能导致结果不同
for(int j=m;j>=1;--j){
if(!flag) dfs(i,j,0);
ans[i][j]=min(ans[i][j],flag?INT_MAX:res);
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)
cout<<(ans[i][j]==INT_MAX ? -1 : ans[i][j])<<" ";
cout<<endl;
}
return 0;
}
C-N皇后问题

Solution
题解见洛谷题单 【算法1-7】搜索 P1219 [USACO1.5]八皇后 Checker Challenge
- TAG:签到题
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,tot,ans[14],lie[14],zhu[25],ci[25];
void dfs(int x){
if(x>n){
++tot;
return;
} else {
for(int i=1;i<=n;++i)
if(lie[i]==0 && ci[i+x-1]==0 && zhu[n-1-i+x]==0){
ans[x]=i;
lie[i]=ci[i+x-1]=zhu[n-1-i+x]=1;
dfs(x+1);
lie[i]=ci[i+x-1]=zhu[n-1-i+x]=0;
}
}
}
int main(){
scanf("%d",&n);
dfs(1);
printf("%d",tot);
return 0;
}
D-生日蛋糕

Solution
ps.题解来自《信息学一本通·提高篇》
【思路点拨】
搜索框架:从下往上搜索,枚举搜索面对的状态有:正在搜索蛋糕第\(dep\)层,当前外表面面积\(s\),当前体积\(v\),第\(dep+1\)层的高度和半径。不妨用数组\(h\)和\(r\)分别记录每层的高度和半径。
整个蛋糕的“上表面”面积之和等于最底层的圆面积,可以在第\(M\)层直接累加到\(s\)中。这样第\(M-1\)层往上的搜索中,只需要计算侧面积。
剪枝
①上下界剪枝。
在第\(dep\)层时,只在下面的范围内枚举半径和高度即可。
首先,枚举\(R \in [dep,min \{ \sqrt{N-v},r[dep+1]-1\}]\),
其次,枚举\(H \in [dep,min \{\frac{N-v}{R^2},h[dep+1]-1 \} ]\)。
上面两个区间右边界中的式子可以通过圆柱体积公式\(\pi R^2H=\pi(N-v)\)得到。
对于\(R\),令\(H=1\),可以得到\(R=\sqrt{N-v}\);
对于\(H\),直接移项,可以得到\(H=\frac{N-v}{R^2}\)
②优化搜索顺序。
在上面确定的范围内,使用倒序枚举。
③可行性剪枝。
可以预处理出从上往下前\(i(1\leqslant i\leqslant M)\)层的最小体积和侧面积。显然,当第\(1 \sim i\)层的半径分别取\(1,2,3\cdots i\),高度也分别取\(1,2,3\cdots i\)时,有最小体积与侧面积。
如果当前体积\(v\)加上\(1 \sim dep-1\)层的最小体积大于\(N\),则可以剪枝。
④最优性剪枝一。
如果当前表面积\(s\)加上\(1 \sim dep-1\)层的最小侧面积大于已经搜到的结果,剪枝。
⑤最优性剪枝二。
利用\(h\)与\(r\)数组,\(1 \sim dep-1\)层的体积可表示为
\(1 \sim dep-1\)层的表面积可表示为
因为
1.\(2\sum_{k=1}^{dep-1}h[k]*r[k]\)表示的是上\(k\)层所有蛋糕的侧面积;
2.当前层蛋糕的半径\(r[dep]\)一定大于等于上层蛋糕的半径\(r[k]\);
3.\(\sum_{k=1}^{dep-1}h[k]*r[k]^2\)表示的是上\(k\)层所有蛋糕的体积;
4.对于上\(k\)层蛋糕来说,它的体积一定会大于等于\((n-v)\)即当前所需的剩余蛋糕体积;
所以当\(\frac{2(n-v)}{r[dep]}+s\)大于已经搜到的结果时,可以剪枝。
加人以上五个剪枝后,搜索算法就可以快速求出该问题的最优解。
实际上,搜索算法面对的状态可以看作一个多元组,其中每一元都是问题状态空间中的一个“维度”。例如,本题中的层数\(dep\)、表面积\(S\)、体积\(V\)、第\(dep+1\)层的高度和半径就构成状态空间中的五个维度,其中每一个维度发生变化,都会移动状态空间中的另一个“点”。这些维度通常在题目描述中也有所体现,它们一般在输入变量、限制条件、待求解变量等非常关键的位置出现。读者一定要注意提取这些“维度”,从而设计出合适的搜索框架。
搜索过程中的剪枝,其实就是针对每个“维度”与该维度的边界条件,加以缩放、推导,得出一个相应的不等式,以减少搜索树分支的扩张。例如,本题中的剪枝①、剪枝③和剪枝④,就是考虑与半径、高度、体积、表面积这些维度的上下界进行比较而直接得到的。
为了进一步提高剪枝的效果,除了当前花费的“代价”之外,我们还可以对未来至少需要花费的代价进行预算,这样更容易接近每个维度的上下界。例如,本题中求前\(dep-1\)层最小体积、最小侧面积。剪枝⑤则通过表面积与体积之间的关系,对不等式进行缩放,\(\frac{2(n-v)}{r[dep]}\)这个式子也是对前\(dep-1\)层侧面积的一个估计。这告诉我们在一般的剪枝不足以解决问题时,还可以结合各维度之间的联系得到更加精准的剪枝。
- TAG:数学;搜索;剪枝
PZ.cpp
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
#define inf 1e9+7
int n,m,minv[25],mins[25],ans=inf;
void dfs(int v,int s,int dep,int r,int h){
if(dep==0){ if(v==n) ans=min(ans,s); return; }
if(v+minv[dep-1]>n) return; //③可行性剪枝
if(s+mins[dep-1]>ans) return; //④最优性剪枝一
if(2*(n-v)/r+s>=ans) return; // ⑤最优性剪枝二
for(int nowh,i=r-1;i>=dep;--i){ //①上下界剪枝 ②优化搜索顺序
if(dep==m) s=i*i;
nowh=min((n-v-minv[dep-1])/(i*i),h-1);
for(int j=nowh;j>=dep;--j)
dfs(v+i*i*j,s+2*i*j,dep-1,i,j);
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=20;++i){ //预处理最小面积和体积
minv[i]=minv[i-1]+i*i*i;
mins[i]=mins[i-1]+2*i*i;
}
dfs(0,0,m,n+1,n+1);
if(ans==inf) puts("0");
else printf("%d",ans);
return 0;
}
E-小木棍
Solution
ps.题解来自《信息学一本通·提高篇》
从题意来看,要得到原始最短木棍的可能长度,可以按照分段数的长度,依此枚举所有的可能长度\(len\);每次枚举\(len\)时,用深度搜索判断是否能用截断后的木棍拼合出整数个\(len\),能用的话,找出最小的\(len\)即可。对于\(1S\)的时间限制,用不加任何剪枝的深度搜索时,时间效率为指数级,效率非常低,程序运行将严重超时。对于此题,可以从可行性和最优性上加以剪枝。
从最优性方面分析,可以做出以下两种剪枝:
①设所有木棍的长度和是\(sum\),那么原长度(也就是需要输出的长度)一定能够被\(sum\)整除,不然就没法拼了,即一定要拼出整数根。
②木棍原来的长度一定大于等于所有木棍中最长的那根。
综合上述两点,可以确定原木棍的长度\(len\)在最长木棍的长度与\(sum\)之间,且\(sum\)能被\(len\)整除。所以,在搜索原木棍的长度时,可以设定为从截断后所有木棍中最长的长度开始,每次增加长度后,必须能整除\(sum\)。这样可以有效地优化程序。
从可行性方面分析,可以再做以下七种剪枝:
①一根长木棍肯定比几根短木棍拼成同样长度地用处小,即短小地可以更灵活组合,所以可以对输入地所有木棍按长度从大到小排序。
②在截断后地排好序地木棍中,当用木棍\(i\)拼合原始木棍时,可以从第\(i+1\)后地木棍开始搜,因为根据优化①,\(i\)前面的木棍已经用过了。
③用当前最长长度的木棍开始搜,如果拼不出当前设定的原木棍长度\(len\),则直接返回,换一个原始木棍长度\(len\)
④相同长度的木棍不要搜索多次。用当前长度的木棍搜下去得不出结果时,用一支同样长度的还是得不到结果,所以,可以提前返回。
⑤判断搜到的几根木棍组成的长度是否大于原始长度\(len\),如果大于,没必要搜下去,可以提前返回。
⑥判断当前剩下的木棍根数是否够拼成木棍,如果不够,肯定拼合不成功,直接返回。
⑦找到结果后,在能返回的地方马上返回到上一层的递归处。
- TAG:搜索;剪枝
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define inf 1e9+7
int a[51],n,m,tot,mina=inf,maxa;
void dfs(int rec,int sum,int now,int p,int q){
//rec为剩余需要拼出的木棍数量,sum为当前长度,now为预计长度,
//p为当前木棍长度,q为下一个木棍长度(使用离散数组代替排序)
if(rec==0){ printf("%d",now); exit(0); }
while(!a[q]) --q; p=min(p,q);
if(sum==now){ dfs(rec-1,0,now,q,q); return; }
for(int i=min(p,now-sum);i>=mina;--i)
if(a[i]&&i+sum<=now){
--a[i];
dfs(rec,sum+i,now,i,q);
++a[i];
if(sum==0||sum+i==now) break;
}
}
int main(){
scanf("%d",&n);
for(int x,i=1;i<=n;++i){
scanf("%d",&x);
if(x>50) continue;
++a[x]; tot+=x;
maxa=max(maxa,x);
mina=min(mina,x);
}
for(int i=maxa;i<=tot>>1;++i) //因为一定木棍砍成的,最大长度即为tot/2
if(tot%i==0)
dfs(tot/i,0,i,maxa,maxa);
printf("%d",tot);
return 0;
}
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
bool cmp(int x,int y){ return x>y; }
int a[105],n,m,len,minlen,sum;
bool used[105],flag;
void dfs(int k,int last,int rest){
//k为第k根木棍,last为第k根上一节木棍编号,rest为第k根木棍还需要的长度
if(k==m){ flag=1; return; }
int i;
if(rest==0){
for(i=1;i<=n;++i)
if(!used[i]){ used[i]=1; break; }
dfs(k+1,i,len-a[i]);
}
for(i=last+1;i<=n;++i)
if(!used[i]&&rest>=a[i]){
used[i]=1;
dfs(k,i,rest-a[i]);
used[i]=0;
int j=i;
while(i<n&&a[i]==a[j]) ++i;
if(i==n) return;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
minlen<a[i]? minlen=a[i] :233;
sum+=a[i];
}
sort(a+1,a+1+n,cmp);
for(int i=minlen;i<=sum;++i)
if(sum%i==0){
memset(used,0,sizeof(used));
len=i;
used[1]=1;
flag=0;
m=sum/i;
dfs(1,1,len-a[1]);
if(flag){ printf("%d",len); break; }
}
return 0;
}
F-在地铁和人海

PZ's Knowledge
ps.以下知识点摘自《信息学奥赛一本通·提高篇》
质数
一、定义
如果大于\(1\)的正整数\(p\)仅有正因子\(1\)和\(p\),则称\(p\)为质数(或者素数);大于\(1\)又不是质数的正整数称为合数。
注意:\(1\)既不是质数,也不是合数;\(2\)是最小的质数,且为唯一的偶质数。质数的个数是无限的。
二、定理
1.算术基本定理
任何一个大于\(1\)的正整数都能唯一分解为有限个质数的乘积,可写作:
其中\(c_i\)都是正整数,\(P_i\)都是质数且满足\(P_1<P_2<\cdots <P_n\)。
2.质数分布定理
对正实数\(x\),定义\(\pi(x)\)为不大于\(x\)的质数个数,则有:\(\pi(x)\approx \frac{x}{lnx}\)。
由质数定理可以给出第\(n\)个质数\(P(n)\)的渐近估计:\(P(n)\approx n*lnn\)。
有结论:一个数\(N\)至多由一个大于\(\sqrt N\)的质因子。
证明:假设\(a,b\)是由\(N\)分解出的两个质因子,且\(a,b > \sqrt N\),那么\(a*b\)是\(N\)的因子,然而\(a*b>N\),所以\(a*b\)不可能是\(N\)的因子,所以原命题成立。
约数
一、整除
整除与约数:设\(a,b\)是两个整数,且\(b \ne 0\),如果存在整数\(c\),使\(a=b*c\),则称\(a\)被\(b\)整除,或\(b\)整除\(a\),记作\(b | a\)。此时,又称\(a\)是\(b\)的倍数,\(b\)是\(a\)的因子。
设\(a,b\)是两个正整数,且\(b \ne 0\),则存在唯一的整数\(q\)和\(r\),使
这个式子叫带余除法,并记余数 \(r=a \;mod \;b\)。例如\(3 \;mod \;2=1\)。
整除具有如下性质:
①若\(a|b\)且\(a|c\),则\(\forall x,y\),有\(a|x*b+y*c\)
②若\(a|b\)且\(b|c\),则\(a|c\)
③设\(m \ne 0\),则\(a|b\),当且仅当\(ma|mb\)
④若\(a|b\)且\(b|a\),则\(a=\pm b\)
二、约数
算术基本定理的推论
在算数基本定理中,若正整数\(N\)被唯一分解为\(N=P_1^{c_1}*P_2^{c_2}*\cdots *P_n^{c_n}\),其中\(c_i\)都是正整数,\(P_i\)都是质数且满足\(P_1<P_2<\cdots <P_n\),则\(N\)的正约数集合可写作:
\(N\)的正约数个数为:
\(N\)的所有正约数的和为:
若\(d \geqslant \sqrt N\)是\(N\)的约数,则\(\frac{N}{d}\leqslant \sqrt N\)也是N的约数。换而言之,约数总是成对出现的(除了对于完全平方数,\(\sqrt N\)会单独出现)。
PZ's solution
思路借鉴于杜宇一声的BZOJ3629 聪明的燕姿 【例题精讲】
1.题目要求很简单,找到所有的正整数\(x\),要求\(x\)的正约数和为\(s\);
2.观察所有正约数的和的式子,可以发现,\((P_n^0+P_n^1+P_n^2+\cdots+P_n^{c_n})\)是成块出现的,我们可以使用深搜来寻找这些块,让\(s\)除掉它,然后寻找其他合法块,直到\(s\)被除为\(1\),则深搜完毕;
3.设找到的某个合法块大小为\(res\),剩余所有合法块乘积为\(ans\),可以发现一种合法答案即为\(res*ans\);
4.特殊的,如果\(s-1\)为质数,则\(s-1\)的所有正约数和为\((s-1)^0+(s-1)^1=1+s-1=s\),就可以直接累加到答案中;
应用合法块的概念,当\(s\)是被除过的情况时,一种合法答案即为\(res*(s-1)\),其实即为\(s-1\)是通过特判快速找到的合法块;
- TAG:数论;质数;约数;搜索
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 50005
//sqrt(2*10^9)约为44721
int p[N],s,ans[N];
bool vis[N];
//线性筛质数
void init(){
vis[0]=vis[1]=1;
for(int i=2;i<N;++i){
if(!vis[i]) p[++p[0]]=i;
for(int j=1;p[j]*i<N;++j){
vis[p[j]*i]=1;
if(i%p[j]==0) break;
}
}
}
//判断质数,为了判断s-1是否为质数而存在,s-1可能大于sqrt(2*10^9)
bool check(int x){
if(x<N) return !vis[x];
for(int i=1;p[i]*p[i]<=x&&i<=p[0];++i)
if(x%p[i]==0) return 0;
return 1;
}
void dfs(int tmp,int res,int s){
//tmp为当前筛到的质数数组的下标,res为合法块累乘的结果,s为剩余需要拼凑的约数和
if(s==1){ ans[++ans[0]]=res; return; }
//找到一种所有合法块都找到的情况,此时累乘得到的res即为答案
if(s-1>=p[tmp]&&check(s-1)) ans[++ans[0]]=res*(s-1);
//对s-1情况的特判
//Q:既然对s-1情况进行特判,不用担心之后搜索合法块,把s-1也搜索到造成答案重复吗?
//A: (1)有可能出现 s-1 > sqrt(最初s) 的情况,所以应该有
// (2)因为确保p[i]*[i]<=s,所以之后的合法块必然遍历不到s-1这样一个大质数,
// 这是一种合法块搜索过程中的一个盲区,所以才需要这个特判
for(int i=tmp;p[i]*p[i]<=s;++i)
for(int j=1+p[i],t=p[i];j<=s;t*=p[i],j+=t)
if(s%j==0) dfs(i+1,res*t,s/j);
//对于当前筛到的质数,遍历其可能的合法块
//Q:为什么是j<=s?
//A:因为可能出现j=s的情况,让s%j==0
}
int main(){
init();
scanf("%d",&s);
dfs(1,1,s);
printf("%d\n",ans[0]);
if(ans[0]){
sort(ans+1,ans+1+ans[0]);
for(int i=1;i<=ans[0];++i)
printf("%d ",ans[i]);
}
return 0;
}
赛后感言
1.这次就A了A题和C题,其实不太应该,在B题上死磕了很多时间,因为错误的搜索方式的思维,导致浪费了许多时间;
2.就题目难度而言,B题、D题是不大好想的,F题是一个不错的数论模板题,倒是B~F题都来自于《信息学奥赛一本通·提高篇》,倒是我没想到的;
3.这次大家成绩都比较惨淡,甚至为此调整了集训方案,但蓝桥杯近在眼前,需要抓紧努力了;
ps.回家忘记带51开发板了,后面的内容看来暂时学不了了,不过stm32开发板马上就到了,新的学习旅程要来了(~ ̄▽ ̄)~
ps.ps.OI赛制下,我居然B题能水33分,虽然我连样例都过不了(⌐■_■),果然水分才是王道。

 新年新气象,从第一次集训比赛题解开始(o゜▽゜)o☆,这次可谓全力以赴!!!!
新年新气象,从第一次集训比赛题解开始(o゜▽゜)o☆,这次可谓全力以赴!!!!

 浙公网安备 33010602011771号
浙公网安备 33010602011771号