使用堆排序 (用 0元素 和 不用 0 元素的区别)
向上调整法和向下调整法有什么区别和联系?
向上调整是由空堆,逐个插入元素,来建立初始堆,向下调整是从n/2的位置,倒着将编内号n/2,n/2-1,...,1直到编号为容1的结点调成堆后,初始堆构建完成。它们没有多大的区别,只不过初始堆有些元素所在的位置不同而已。
建成最大堆后, 每一个父子链都是 父 > 子, 如果有反过来的,说明交换过程出现错误, 如下图: 父节点 1 的值肯定大于其子节点 2 或者 3 的值.
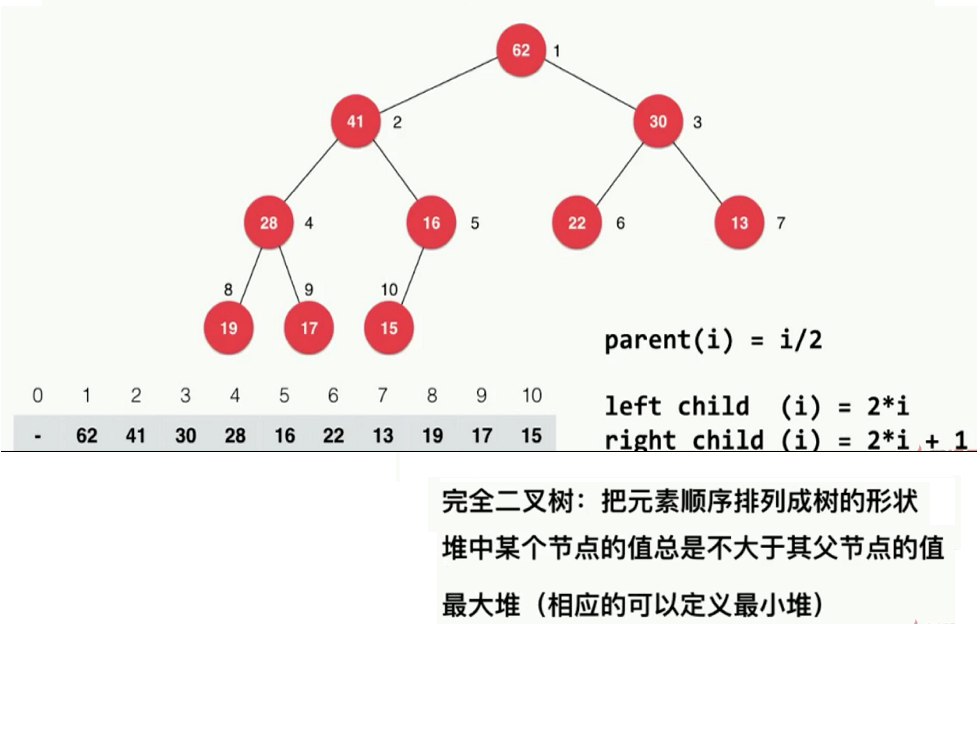
使用 arr[0] 和 arr[1] 的堆排序 , 主要的区别在下面三个函数 :
heapSort --- 完成堆排序的入口函数
buildHeap --- 完成堆顶(最大最小元素)的查找,即堆顶第一个元素肯定是最大或者最小
adjustHeap --- 堆的调整
1. start from arr[2]
heap_size 的计算 ,//完全二叉树的最后一个非叶子结点, 比如 (4,5) 的父节点是 2
// 数组从 1,2,3,... 开始有效
#include "common.h"
//交换堆中任意两个数
static void Swap(int arr[], int from, int to)
{
int temp = arr[from];
arr[from] = arr[to];
arr[to] = temp;
}
//打印堆中的数据
static void printHeap(int arr[], int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
/**
* heap_size 此次调整堆的最大元素个数(因为堆排序过程中,后面已经调整好的就不需要调整了)
* i 表示此次调整堆的父节点
* */
#if 1
static void adjustHeap(int arr[], int i, int heap_size)
{
int left = 2 * i; //获得该父节点的左孩子
int right = 2 * i + 1; //获得该父节点的右孩子
int maxpos = i;
while (left <= heap_size) //must use <=
{
if (arr[left] > arr[maxpos])
{
maxpos = left;
}
if (right <= heap_size && arr[right] > arr[maxpos]) //must use <=
{
maxpos = right;
}
if (maxpos != i)
{
Swap(arr, i, maxpos);
i = maxpos; //继续向下调整,因为此次调整可能会破坏原来下面的堆
left = 2 * i;
right = 2 * i + 1;
}
else
{
break;
}
}
}
#else
static void adjustHeap(int arr[], int i, int heap_size)
{
int left = 2 * i;//获得该父节点的左孩子
int right = 2 * i + 1;//获得该父节点的右孩子
int maxpos = i;
if (left <= heap_size && arr[left] > arr[maxpos]) //must use <=
{
maxpos = left;
}
if (right <= heap_size && arr[right] > arr[maxpos]) //must use <=
{
maxpos = right;
}
if (maxpos != i)
{
Swap(arr, i, maxpos);
adjustHeap(arr, maxpos, heap_size); //继续向下调整,因为此次调整可能会破坏原来下面的堆
}
}
#endif
//第一次建堆的过程
static void buildHeap(int arr[], int heap_size)
{
int len = heap_size / 2; //完全二叉树的最后一个非叶子结点, 比如 (4,5) 的父节点是 2
for (int i = len; i >= 1; i--) // 数组从 1,2,3,... 开始有效
{
adjustHeap(arr, i, heap_size);
}
}
static void heapSort(int arr[], int len)
{
buildHeap(arr, len); //首次建堆,建成一个完整的大顶堆(根节点为最大值)
printHeap(arr, len);
for (int heap_size = len - 1; heap_size >= 2;)
{
Swap(arr, 1, heap_size);//将堆顶元素(通过调整堆获得的最大值)和最后一个交换(剩余未排好序部分的最后一个)
heap_size--;
adjustHeap(arr, 1, heap_size);//之后每次从堆顶开始调整,最大的值将上升到根节点
}
}
extern void test_heap_not_use0()
{
int arr[] = { 20,14,10,8,7,9,3,2,4,1,80,50,40,70,11,19,12,18,23,35,22 }; // 这个不考虑 0 号元素, 可能好一点
int len = sizeof(arr) / sizeof(arr[0]); // no need to consider number 0, so the len is 9 only
printf("%s %d : arr len = %d \n", __FUNCTION__, __LINE__, len);
heapSort(arr, len);
printHeap(arr, len);
}
2. start from arr[0]
heap_size 的计算 , int len = heap_size / 2 - 1; //完全二叉树的最后一个非叶子结点, 比如 (3,4) 的父节点是 1
for (int i = len; i >= 0; i--) // 数组从 0, 1,2,3,... 开始有效
#include "common.h"
//交换堆中任意两个数
static void Swap(int arr[], int from, int to)
{
int temp = arr[from];
arr[from] = arr[to];
arr[to] = temp;
}
//打印堆中的数据
static void printHeap(int arr[], int len)
{
for (int i = 0; i < len; i++)
{
printf("%d ", arr[i]);
}
printf("\n");
}
/**
* heap_size 此次调整堆的最大元素个数(因为堆排序过程中,后面已经调整好的就不需要调整了)
* i 表示此次调整堆的父节点
* */
#if 1
static void adjustHeap(int arr[], int i, int heap_size)
{
int left = 2 * i + 1; //获得该父节点的左孩子
int right = 2 * i + 2; //获得该父节点的右孩子
int maxpos = i;
while (left < heap_size) //if use <= , fail as the max data is arr[heap_size-1]
{
if (arr[left] > arr[maxpos])
{
maxpos = left;
}
if (right < heap_size && arr[right] > arr[maxpos])
{
maxpos = right;
}
if (maxpos != i)
{
Swap(arr, i, maxpos);
i = maxpos; //继续向下调整,因为此次调整可能会破坏原来下面的堆
left = 2 * i + 1;
right = 2 * i + 2;
}
else
{
break;
}
}
}
#else
static void adjustHeap(int arr[], int i, int heap_size)
{
int left = 2 * i + 1;//获得该父节点的左孩子
int right = 2 * i + 2;//获得该父节点的右孩子
int maxpos = i;
//here left and right should < heap_size
if (left < heap_size && arr[left] > arr[maxpos]) // i=10, heap_size=21, left = 21,right = 22, arr[left] and arr[right] out of bound
{
maxpos = left;
}
if (right < heap_size && arr[right] > arr[maxpos])
{
maxpos = right;
}
if (maxpos != i)
{
Swap(arr, i, maxpos);
adjustHeap(arr, maxpos, heap_size); //继续向下调整,因为此次调整可能会破坏原来下面的堆
}
}
#endif
//第一次建堆的过程
static void buildHeap(int arr[], int heap_size)
{
int len = heap_size / 2 - 1; //完全二叉树的最后一个非叶子结点, 比如 (3,4) 的父节点是 1
for (int i = len; i >= 0; i--) // 数组从 0, 1,2,3,... 开始有效
{
adjustHeap(arr, i, heap_size);
}
}
//堆排序函数
static void heapSort(int arr[], int len)
{
buildHeap(arr, len); //首次建堆,建成一个完整的大顶堆(根节点为最大值)
printHeap(arr, len);
for (int heap_size = len - 1; heap_size >= 1;)
{
Swap(arr, 0, heap_size); //将堆顶元素(通过调整堆获得的最大值)和最后一个交换(剩余未排好序部分的最后一个)
heap_size--;
adjustHeap(arr, 0, heap_size); //之后每次从堆顶开始调整,最大的值将上升到根节点
}
}
extern void test_heap_use0()
{
int arr[] = { 20,14,10,8,7,9,3,2,4,1,80,50,40,70,11,19,12,18,23,35,22 }; // 这个不考虑 0 号元素, 可能好一点
int len = sizeof(arr) / sizeof(arr[0]);
printf("%s %d : arr len = %d \n", __FUNCTION__, __LINE__, len);
heapSort(arr, len);
printHeap(arr, len);
}
使用 compare 可以快速看出来差异.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号