FJOI 2020 Day1 T3 异构序列码性态问题

题意简述

有两个序列 \(a, b\) 以及两个辅助栈 \(s_1, s_2\)。

初始时 \(a\) 的元素依次为 \([1, 2, 3, \ldots , n]\)，而 \(s_1, s_2, b\) 均为空。

每次可以执行如下三种操作之一：

1. 若 \(a\) 非空，将 \(a\) 的最后一个元素删除，插入到第一个栈 \(s_1\) 的栈顶。
2. 若 \(s_1\) 非空，将 \(s_1\) 的栈顶弹出，插入到第二个栈 \(s_2\) 的栈顶。
3. 若 \(s_2\) 非空，将 \(s_2\) 的栈顶弹出，插入到序列 \(b\) 的第一个元素之前。

需要特别注意的是，任意时刻必须保证 \(s_2\) 从栈顶到栈底的序列是递减的。

当所有元素均被插入到序列 \(b\) 中，停止操作，我们称得到了序列 \(b\)。

请问在所有的 \(n!\) 种 \(1 \sim n\) 的排列中，有哪些是不能在这个过程中得到的。

样例：当 \(n \le 3\) 时答案为 \(0\)，当 \(n = 4\) 时答案为 \(2\)。

题解

考虑统计能够得到的序列 \(b\) 的个数，最后用 \(n!\) 减去。

分析序列 \(b\) 需要满足的性质，通过手动枚举发现当 \(n = 4\) 时仅有这两个序列不能被得到：

1. 序列 \([3, 1, 4, 2]\)。
2. 序列 \([3, 2, 4, 1]\)。

同时我们可以写出一个，给出最终序列 \(b\)，判断它是否能被得到的程序，每次贪心地用最少的步数把目标元素移到 \(b\) 的开始即可。

利用这个程序，枚举所有的全排列，我们容易得到 \(n = 5\) 或更大时，无法被得到的序列。

稍加观察能够发现，它们也都满足性质：存在不一定连续的子序列，满足其中的元素离散化后依次等于 \([3, 1, 4, 2]\) 或 \([3, 2, 4, 1]\)。

为了更准确地验证，可以写一个 \(\mathcal O (n^4)\) 枚举子序列并判断的程序，枚举全排列就能验证这个性质。

所以得到唯一的性质：\(b\) 中不存在任何子序列满足其中的元素离散化后依次等于 \([3, 1, 4, 2]\) 或 \([3, 2, 4, 1]\)。

我们考虑按照值从小到大加入元素，一开始为空序列，然后依次加入 \(1, 2, 3, \ldots\)。

观察到在此时前面的条件就等价于，在某个位置插入当前的数后，之后就不能在这个位置后面的元素中的空隙中插入更大的元素了。

这是因为当前时刻前插入的数都比当前数小，对应 \(1, 2\)，而当前数对应 \(3\)，当前时刻后插入的数对应 \(4\)，不能在 \(1, 2\) 之间插入。

举个例子：

1. \(\left[ \boxed{1} \right]\)。
2. \(\left[ \boxed{2}, \boxed{1} \right]\)。
3. \(\left[ \boxed{3}, \boxed{2, 1} \right]\)。
4. \(\left[ \boxed{3}, \boxed{2, 1}, \boxed{4} \right]\)。
5. \(\left[ \boxed{3}, \boxed{5}, \boxed{2, 1, 4} \right]\)。
6. \(\left[ \boxed{3}, \boxed{5}, \boxed{2, 1, 4}, \boxed{6} \right]\)。
7. \(\left[ \boxed{7}, \boxed{3, 5, 2, 1, 4, 6} \right]\)。

也就是，如果已经确定一段元素中间不能插入其它元素了，那么就把它们用方框框住。

这导出一个 DP 方程：令 \(\mathrm{f}[i][j]\) 表示目前加入了 \(1 \sim i\)，并且当前有 \(j\) 个方框时的方案数。

当 \(n \ge 2\) 时，有边界条件 \(\mathrm{f}[2][2] = 2\) 以及转移方程：

\[\begin{aligned} \mathrm{f}[i][j] &\to_+ \mathrm{f}[i + 1][k] : \mathrm{Coef} \\ \mathrm{Coef} &= \begin{cases} 1 & , 2 \le k \le j \\ 2 & , k = j + 1 \\ 0 & , \text{otherwise} \end{cases} \end{aligned} \]

暴力转移得到 \(\mathcal O (n^3)\) 的做法。

还可以得到 \(\mathrm{f}[i][j] = \mathrm{f}[i][j + 1] + 2 \mathrm{f}[i - 1][j - 1] - \mathrm{f}[i - 1][j]\)，得到 \(\mathcal O (n^2)\) 的做法，这个递推式将会是接下来的关键。

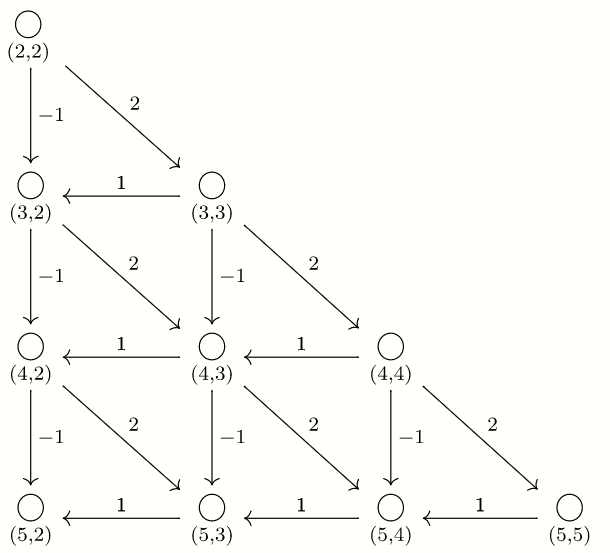
观察上图，可以发现就是递推式的图形化体现，\(\mathrm{f}[i][j]\) 的值为上图中从 \((2, 2)\) 走到 \((i, j)\) 的带权路径数量乘以 \(2\)。

要求的即是对于所有 \(2 \le i \le n\)，从 \((2, 2)\) 走到 \((n, i)\) 的带权路径数量之和乘以 \(2\)。

一个观察：对于一行的从 \((2, 2)\) 走到 \((n, i)\) 的带权路径数量之和，等于从 \((2, 2)\) 走到 \((n + 1, 2)\) 的带权路径数量。

所以要求从 \((2, 2)\) 走到 \((n + 1, 2)\) 的带权路径数量，乘以 \(2\) 就是能被得到的序列 \(b\) 的数量。

令上图中的下标都偏移 \(-2\)，即从 \((0, 0)\) 开始，到达 \((n - 1, 0)\) 的方案数。

令 \(n' = n - 1\)，所求即是 \(\displaystyle \sum_{i = 0}^{n'} 2^i {(-1)}^{n' - i} \binom{n' + i}{n' - i} C_i\)，其中 \(C_i\) 为卡特兰数，\(C_1 = 1, C_2 = 2, C_3 = 5\)。

意义为枚举往右下走了 \(i\) 步，则往下是 \((n' - i)\) 步，贡献 \(2^i {(-1)}^{n' - i}\)。

不同的走法有 \(C_i\) 种，插入向下走的 \(n' - i\) 步有 \(\displaystyle \binom{n' + i}{n' - i}\) 种方法。