LOJ 3185: 「CEOI2018」斐波那契表示法
题目传送门:LOJ #3185。
题意简述:
题目说得很清楚了。
题解:
首先需要了解「斐波那契数系」为何物。
按照题目中定义的斐波那契数列 \(F_n\),可以证明,每个非负整数 \(n\) 都能够以唯一方式用如下方式描述:
其中 \(m\) 是正整数,\(a\) 是长度为 \(m\) 的 \(01\) 序列,\(a\) 中不存在相邻两项 \(a_i\) 与 \(a_{i+1}\) 同为 \(1\)。
例如,当 \(m=5\) 时,有:
对斐波那契数系更详细的解释可以在《具体数学》(人民邮电出版社)的第 248 页找到。
将某个正整数 \(n\) 以这种方式表示后,可以方便地计算 \(X(n)\) 的值:
-
可以发现一个 \(1\) 可以变成低位的两个 \(1\),事实上,形如 \(\overline{1000\cdots000}\) 的数的 \(X\) 函数值应为 \(1\) 的位置加 \(1\) 除以 \(2\) 向下取整。
例如 \(X(\overline{10000000})=\left\lfloor\frac{9}{2}\right\rfloor=4\),即 \(X(34)=4\)。 -
进一步地,假设 \(a\) 中为 \(1\) 的位置依次为 \(b_1,b_2,\ldots,b_k\),并且令 \(b_0=0\)。
-
令 \(f_i\) 为只考虑前 \(i\) 个 \(1\),且不将第 \(i\) 个 \(1\)(即位置 \(b_i\) 上的 \(1\))变成低位的两个 \(1\) 时的方案数(此时最高位为 \(b_i\))。
令 \(g_i\) 为只考虑前 \(i\) 个 \(1\),且将第 \(i\) 个 \(1\)(即位置 \(b_i\) 上的 \(1\))变成低位的两个 \(1\) 时的方案数(此时最高位为 \(b_i-1\))。 -
经过观察(打表)并综合上面的结论,可以得出:
\(f_i=f_{i-1}+g_{i-1},g_i=\left\lfloor\frac{b_i-b_{i-1}-1}{2}\right\rfloor\cdot f_{i-1}+\left\lfloor\frac{b_i-b_{i-1}}{2}\right\rfloor\cdot g_{i-1}\)。 -
边界条件是 \(f_0=1,g_0=0\)。
答案为 \(f_k+g_k\)。
令 \(b\) 的差分数列为 \(d\),即 \(d_i=b_i-b_{i-1}\)。
则可以简单地将转移写成矩阵的形式:
那么,只要能够维护 \(d_i\) 及其对应的矩阵乘积序列,就可以求得答案。
因为有类似在中间插入的操作,可以考虑使用平衡树维护。
在下文的代码中,我使用了无旋 Treap 来维护矩阵序列。
接下来考虑某个插入某个 \(F_i\) 的操作会对 \(d\) 产生何种影响:
一、如果 \(a_{i-1},a_i,a_{i+1}\) 均为 \(0\),即加入 \(F_i\) 不影响 \(a\) 的合法性:
那么就直接加入 \(F_i\),令 \(a_i=1\),并相对应地修改 \(d\) 数列。
二、否则会影响 \(a\) 的合法性,经过细致的分类讨论与归纳(找规律)后:
发现插入时不同的特征,会导致三类不同的结果,而且与形如 \(\overline{10101\cdots101}\) 的极大的 \(01\) 交替的子串有密切关系,如图所示:
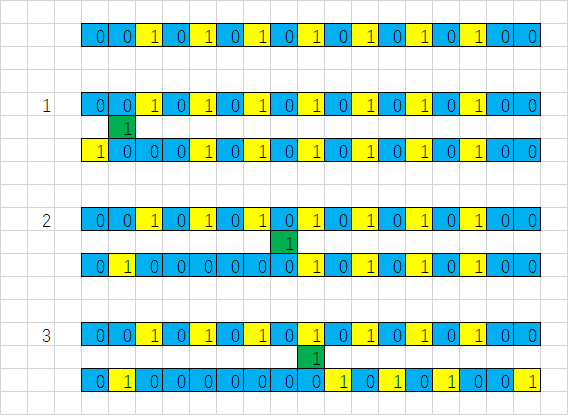
原序列 \(a\) 中一段长度为 \(13\) 的极大的 \(01\) 交替子串(有 \(7\) 个 \(1\))被截取了下来(左侧是高位,右侧是低位);
其中 \(0\) 所在的位置被染成蓝色,\(1\) 所在的位置被染成黄色,新加入的 \(1\) 被染成绿色。
具体推导过程这里不再详述,读者可以反复使用如下两个等式,以对结论进行验证:
主要有三种本质不同的情况:
(为了表示方便,令 \(\mathrm{high}\) 为交替子串的最高位,\(\mathrm{low}\) 为交替子串的最低位,\(\mathrm{pos}\) 为新加入的 \(1\) 的位置)
(显然有 \(\mathrm{low}\equiv\mathrm{high}\pmod{2}\) 和 \(\mathrm{low}-1\le\mathrm{pos}\le\mathrm{high}+1\))
-
\(\mathrm{pos}=\mathrm{high}+1\):
修改 \(a_{\mathrm{high}}\) 为 \(0\),修改 \(a_{\mathrm{high}+2}\) 为 \(1\),并相对应地修改 \(d\) 数列。
注意这里的修改 \(a_{\mathrm{high}+2}=1\) 可能造成连锁反应,需要「递归」处理(稍后将揭示递归只会重复常数层)。 -
\(\mathrm{low}-1\le\mathrm{pos}\le\mathrm{high}\) 且 \(\mathrm{pos}\not\equiv\mathrm{high}\pmod{2}\):
修改 \(a_{\mathrm{pos}+1},a_{\mathrm{pos}+3},\ldots,a_{\mathrm{high}}\) 为 \(0\),修改 \(a_{\mathrm{high}+1}\) 为 \(1\),并相对应地修改 \(d\) 数列。 -
\(\mathrm{low}-1\le\mathrm{pos}\le\mathrm{high}\) 且 \(\mathrm{pos}\equiv\mathrm{high}\pmod{2}\):
修改 \(a_{\mathrm{pos}},a_{\mathrm{pos}+2},\ldots,a_{\mathrm{high}}\) 为 \(0\),修改 \(a_{\mathrm{high}+1}\) 为 \(1\);
修改 \(a_{\mathrm{pos}-2},a_{\mathrm{pos}-4},\ldots,a_{\mathrm{low}}\) 为 \(0\),修改 \(a_{\mathrm{pos}-1},a_{\mathrm{pos}-3},\ldots,a_{\mathrm{low}+1}\) 为 \(1\);
最后修改 \(a_{\mathrm{low}-2}\) 为 \(1\),并相对应地修改 \(d\) 数列。
注意此处涉及的修改比较复杂,但是可以发现区间 \([\mathrm{low},\mathrm{pos}-1]\) 的修改可以看作是向高位整体移动了 \(1\) 位,对 \(d\) 的影响不大。
注意这里的修改 \(a_{\mathrm{low}-2}=1\) 可能造成连锁反应,需要「递归」处理(稍后将揭示递归只会重复常数层)。
先不考虑上文提到的「递归」,分析一下上述三种情况对 \(d\) 数列的改变。
可以发现形式均为:删除一段 \(d\) 中的元素,并加入(或修改)常数个 \(d\) 中的元素。
这两种操作都是可以用无旋 Treap 维护的,且因为每次加入(或修改)仅常数个元素,所以这部分的时间复杂度为期望 \(\mathcal{O}(n\log n)\)。
考虑到可能发生连锁反应,实际上这并不需要担心,稍加分析就可发现:
第一种情况造成的连锁反应只可能触发第二种情况,而第二种情况是不会发生连锁反应的。
第三种情况造成的连锁反应只可能触发第一种情况,而因为 \(a_{\mathrm{low}}\) 变为了 \(0\),所以不会触发进一步的连锁反应。
上面的分析中还涉及到一个问题:如何提取被新加入的 \(F_i\) 影响的 \(01\) 交替子串?
比较方便的是使用 std::set< structure > 维护,其中 structure 是自定义的结构体,具有存储一段极大 \(01\) 交替子串的功能。
在做上述修改的时候,不难发现对极大 \(01\) 交替子串的影响也是 \(\mathcal{O}(1)\) 的,故这部分也可以在 \(\mathcal{O}(n\log n)\) 内实现。
要格外注意实现细节,包括删除子串的一部分,合并新出现的相邻的极大 \(01\) 交替子串等。
令人欣喜的是,本题中需要合并相邻的交替子串的情况,仅可能由新加入单个 \(1\) 导致。
这是因为「情况三」中,整段的连续子串的移动是「向内」的。
下面是代码,如上文所述,时间复杂度为期望 \(\mathcal{O}(n\log n)\),需要格外注意实现细节:
#include <cstdio>
#include <algorithm>
#include <set>
#include <cctype>
inline int read() {
int x = 0; char ch;
while (!isdigit(ch = getchar())) ;
while (x = x * 10 + (ch & 15), isdigit(ch = getchar())) ;
return x;
}
inline void write(int x) {
if (!x) putchar('0');
static char s[11]; int t = 0;
while (x) s[++t] = (x % 10) | 48, x /= 10;
while (t) putchar(s[t--]);
putchar('\n');
} // IO template
typedef long long LL;
const int Mod = 1000000007;
const int Inf = 0x3f3f3f3f;
const int MS = 200005; // 2 * MN
int N;
// No-Rotation Treap
inline unsigned ran() {
static unsigned x = 23333;
return x ^= x << 13, x ^= x >> 17, x ^= x << 5;
}
struct Mat {
#define F(i) for (int i = 0; i < 2; ++i)
int A[2][2];
Mat() {}
Mat(int t) { F(i) F(j) A[i][j] = i == j ? t : 0; }
inline friend Mat operator * (const Mat &p, const Mat &q) {
Mat r; LL A[2][2];
F(i) F(j) A[i][j] = 0;
F(i) F(j) F(k) A[i][k] += (LL)p.A[i][j] * q.A[j][k];
F(i) F(j) r.A[i][j] = A[i][j] % Mod;
return r;
} // Reduce [mod] Times
#undef F
} prd[MS], val[MS];
int Root, pri[MS], ls[MS], rs[MS], dif[MS], sdf[MS], cnt;
inline void NMdf(int id, int d) { // [id] Is A Leaf
dif[id] = sdf[id] = d;
val[id].A[0][0] = val[id].A[0][1] = 1;
val[id].A[1][0] = (d - 1) / 2, val[id].A[1][1] = d / 2;
prd[id] = val[id];
}
inline int NewNode(int d) { pri[++cnt] = ran(), NMdf(cnt, d); return cnt; }
inline int upd(int id) {
prd[id] = prd[rs[id]] * val[id] * prd[ls[id]];
sdf[id] = sdf[ls[id]] + dif[id] + sdf[rs[id]];
return id;
}
int Merge(int rt1, int rt2) {
if(!rt1) return rt2;
if(!rt2) return rt1;
if (pri[rt1] < pri[rt2]){
rs[rt1] = Merge(rs[rt1], rt2);
return upd(rt1);
}
else {
ls[rt2] = Merge(rt1, ls[rt2]);
return upd(rt2);
}
}
void Split(int rt, int k, int &rt1, int &rt2) {
if (!rt) { rt1 = rt2 = 0; return; }
if(k < sdf[ls[rt]] + dif[rt]) {
Split(ls[rt], k, rt1, rt2);
ls[rt] = rt2, rt2 = upd(rt);
}
else{
Split(rs[rt], k - sdf[ls[rt]] - dif[rt], rt1, rt2);
rs[rt] = rt1, rt1 = upd(rt);
}
}
inline int TMin(int rt) { while (ls[rt]) rt = ls[rt]; return rt; } // Minimum Existing Element, [rt] Exists
inline void TInsert(int pos) { // [pos] Does Not Exist
int rt1, rt2, rt3;
Split(Root, pos, rt1, rt2);
if (!rt2) { Root = Merge(rt1, NewNode(pos - (rt1 ? sdf[rt1] : 0))); return ; }
int lstp = rt1 ? sdf[rt1] : 0, nxtp = lstp + dif[TMin(rt2)];
Split(rt2, nxtp - lstp, rt2, rt3);
NMdf(rt2, nxtp - pos);
Root = Merge(Merge(rt1, NewNode(pos - lstp)), Merge(rt2, rt3));
}
inline void TDelete(int lb, int rb) { // [lb, rb, 2] Exists
int rt1, rt2, rt3, rt4;
Split(Root, rb, rt1, rt3);
Split(rt1, lb - 1, rt1, rt2);
if (!rt3) { Root = rt1; return ; }
int lstp = rt1 ? sdf[rt1] : 0, nxtp = rb + dif[TMin(rt3)];
Split(rt3, nxtp - rb, rt3, rt4);
NMdf(rt3, nxtp - lstp);
Root = Merge(rt1, Merge(rt3, rt4));
}
inline void TShiftString(int lb, int rb) { // [lb, rb, 2] Exists
int rt1, rt2, rt3, rt4, rt5;
Split(Root, rb, rt1, rt4);
Split(rt1, lb - 1, rt1, rt2);
int lstp = rt1 ? sdf[rt1] : 0;
Split(rt2, lb - lstp, rt2, rt3);
NMdf(rt2, lb - lstp + 1);
rt2 = Merge(rt2, rt3);
if (!rt4) { Root = Merge(rt1, rt2); return ; }
int nxtp = rb + dif[TMin(rt4)];
Split(rt4, nxtp - rb, rt4, rt5);
NMdf(rt4, nxtp - rb - 1);
Root = Merge(Merge(rt1, rt2), Merge(rt4, rt5));
}
struct C {
int min, max;
C(int l = 0, int r = 0) : min(l), max(r) {}
inline friend bool operator < (const C &p, const C &q) { return p.max < q.max; }
}; std::set<C> st;
typedef std::set<C>::iterator iter;
inline void Put(int pos) ; // Add Fib[pos]
inline void PutT1(iter it, int pos) {
TDelete(pos - 1, pos - 1);
int nmin = it->min, nmax = it->max;
st.erase(it);
if (nmin != nmax) st.insert(C(nmin, nmax - 2));
Put(pos + 1);
}
inline void PutT2(iter it, int pos) {
int nmax = it->max, nmin = it->min;
TDelete(pos + 1, nmax);
st.erase(it);
if (nmin <= pos - 1) st.insert(C(nmin, pos - 1));
Put(nmax + 1);
}
inline void PutT3(iter it, int pos) {
int nmax = it->max, nmin = it->min;
TDelete(pos, nmax);
st.erase(it);
if (nmin != pos) {
TShiftString(nmin, pos - 2);
st.insert(C(nmin + 1, pos - 1));
}
Put(nmax + 1);
if (nmin != 1) Put(nmin == 2 ? 1 : nmin - 2);
}
inline void Put(int pos) {
iter it = st.lower_bound(C(pos - 1, pos - 1));
if (it->min - 1 <= pos && pos <= it->max + 1) {
if (pos == it->max + 1) PutT1(it, pos);
else if ((it->max - pos) % 2 == 1) PutT2(it, pos);
else PutT3(it, pos);
}
else {
iter nxt = it, lst = it; --lst;
TInsert(pos);
int nmin = pos, nmax = pos;
if (nxt->min == pos + 2) nmax = nxt->max, st.erase(nxt);
if (lst->max == pos - 2) nmin = lst->min, st.erase(lst);
st.insert(C(nmin, nmax));
}
}
int main() {
prd[0] = val[0] = Mat(1);
st.insert(C(Inf, Inf)), st.insert(C(-Inf, -Inf));
N = read();
for (int i = 1; i <= N; ++i) {
Put(read());
write((prd[Root].A[0][0] + prd[Root].A[1][0]) % Mod);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号