AtCoder Grand Contest 001
题目传送门:AtCoder Grand Contest 001。
A - BBQ Easy
不难证明答案为排序后的所有奇数项之和。
#include <cstdio>
#include <algorithm>
const int MN = 205;
int N, A[MN];
int main() {
scanf("%d", &N), N *= 2;
for (int i = 1; i <= N; ++i) scanf("%d", &A[i]);
std::sort(A + 1, A + N + 1);
int Sum = 0;
for (int i = 1; i <= N; i += 2) Sum += A[i];
printf("%d\n", Sum);
return 0;
}
B - Mysterious Light
考虑反射两次之后就形成了平行四边形结构。
之后每反射两次就会让平行四边形长边减去短边的长度。
这是更相减损术,那么用辗转相除法优化即可,时间复杂度 \(\mathcal O (\log N)\)。
#include <cstdio>
typedef long long LL;
LL N, X;
LL f(LL a, LL b) {
return b ? a / b * b * 2 + f(b, a % b) : -a;
}
int main() {
scanf("%lld%lld", &N, &X);
printf("%lld\n", N + f(X, N - X));
return 0;
}
C - Shorten Diameter
枚举留下的树的直径的中点就行啦,如果 \(K\) 是奇数那就枚举边,否则枚举点。
然后直接跑 DFS 进行 check 然后更新答案就行啦,时间复杂度 \(\mathcal O (N^2)\)。
#include <cstdio>
#include <vector>
const int MN = 2005;
int N, K, eu[MN], ev[MN];
std::vector<int> G[MN];
int dep[MN];
void DFS(int u, int p) {
for (int v : G[u]) if (v != p) dep[v] = dep[u] + 1, DFS(v, u);
}
int main() {
scanf("%d%d", &N, &K);
for (int i = 1; i < N; ++i) {
scanf("%d%d", &eu[i], &ev[i]);
G[eu[i]].push_back(ev[i]);
G[ev[i]].push_back(eu[i]);
}
int Ans = N;
if (K & 1) {
for (int i = 1; i < N; ++i) {
int u = eu[i], v = ev[i];
dep[u] = dep[v] = 0;
DFS(u, v), DFS(v, u);
int cnt = 0;
for (int j = 1; j <= N; ++j) if (dep[j] > K / 2) ++cnt;
Ans = Ans > cnt ? cnt : Ans;
}
} else {
for (int i = 1; i <= N; ++i) {
dep[i] = 0, DFS(i, 0);
int cnt = 0;
for (int j = 1; j <= N; ++j) if (dep[j] > K / 2) ++cnt;
Ans = Ans > cnt ? cnt : Ans;
}
}
printf("%d\n", Ans);
return 0;
}
D - Arrays and Palindrome
可以发现,如果一段的长度是 \(x\),就会贡献 \(x / 2\) 条边。
阿勒,其实是错的,如果 \(x\) 是奇数,那其实是 \(x / 2 - 0.5\) 条边。
然而所有的 \(x\) 之和是 \(2 N\) 吧,那么就是正好 \(N\) 条边,但是每有一个奇数的 \(x\) 就减去 \(0.5\) 条边。
因为要让 \(N\) 个点连通至少需要 \(N - 1\) 条边,所以奇数的 \(x\) 的个数最多两个啦。
实际上因为奇偶性的关系,要么是 \(0\) 个要么是 \(2\) 个。
那么我们首先检查 \(A\) 中的奇数个数是否超过两个,如果超过了那必然是 Impossible。
然后我们很容易想到一个这样的构造:
如果 \(a_1\) 和 \(b_1\) 正好相差 \(1\) 的话,那么它们就一奇一偶,稍微推一下就可以发现结构:
正好是从是奇数的那个划分的正中心开始,以一条链左右转来转去,最后到凸出来的那个地方为止。
如果 \(M = 2\) 的话,官方题解中的图片很好地展示了这一点:
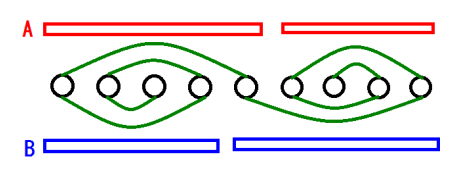
如果 \(M \ge 3\) 呢?如果类比 \(M = 2\) 的情况,我们可能希望除了头尾微调一格,中间的长度不变:
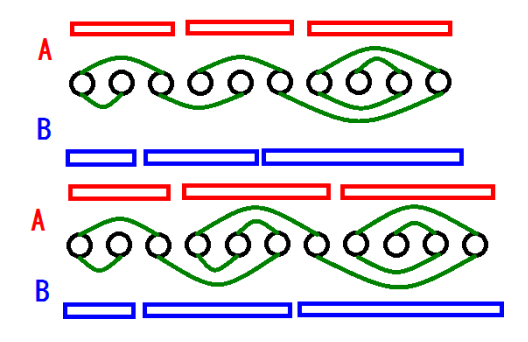
然而这不是一定都可行的,稍加分析我们可以发现:
如果出现 \(a_i = b_i\) 而且它们都是奇数,而且位置正好错开一格,那么整个图就会不连通。
这实际上是与之前的奇数最多两个的结论相符合的,要改变也很简单:
把奇数的段移到 \(a\) 序列的两端即可。因为 \(A\) 中奇数不超过两个,所以这必然是可以办到的。
然后中间的部分都是偶数,稍加分析可以发现,错开一格的两个偶数段,是必然形成一条链的,完美符合要求。
对于 \(M = 1\) 的情况要特殊处理一下,输出 \(1\) 和 \((N - 1)\) 即可。
#include <cstdio>
#include <algorithm>
const int MN = 100005;
int N, M, A[MN];
int main() {
scanf("%d%d", &N, &M);
int C = 0;
for (int i = 1; i <= M; ++i) scanf("%d", &A[i]), C += A[i] & 1;
if (C > 2) return puts("Impossible"), 0;
int p1 = 0, p2 = 0;
for (int i = 1; i <= M; ++i)
if (A[i] & 1) (p1 ? p2 : p1) = i;
if (p1 && !p2) std::swap(A[1], A[p1]);
if (p2) std::swap(A[1], A[p1]), std::swap(A[p2], A[M]);
for (int i = 1; i <= M; ++i) printf("%d%c", A[i], " \n"[i == M]);
if (N == 1) return puts("1\n1"), 0;
if (M == 1) return printf("2\n1 %d\n", N - 1), 0;
--A[1], ++A[M];
printf("%d\n", M - !A[1]);
for (int i = A[1] ? 1 : 2; i <= M; ++i) printf("%d%c", A[i], " \n"[i == M]);
return 0;
}
E - BBQ Hard
也就是要求 \(\displaystyle \sum_{1 \le i < j \le N} \binom{A_i + A_j + B_i + B_j}{A_i + A_j}\)。
考虑二项式系数的几何意义,\(\displaystyle \binom{A + B}{A}\) 就是从 \((0, 0)\) 走到 \((A, B)\) 的方案数(每次让横 / 纵坐标加上 \(1\))。
那么上式中的可以看作是从 \((-A_i, -B_i)\) 走到 \((A_j, B_j)\) 的方案数,然后对所有 \((i, j)\) 求和。
注意到如果我们使用常规的 DP,用类似求杨辉三角的方式递推的话,也是可以求出的。
而且这东西还是线性的,也就是把所有的起点和终点都一起做,某个位置的数值表示从任意一个起点出发走到这个点的方案数。
那么把所有终点的数值相加,求得的就是对所有 \(\displaystyle \sum_{1 \le i, j \le N} \binom{\mathtt{xx}}{\mathtt{xx}}\) 的方案数。
把 \(i = j\) 的扣掉,然后除以 \(2\) 就是真实的答案了。
时间复杂度为 \(\mathcal O (N + (\max A) (\max B))\)。
#include <cstdio>
typedef long long LL;
const int Mod = 1000000007, Inv2 = (Mod + 1) / 2;
const int MN = 200005, C = 2000, O = C + 1, MS = O + C + 1;
inline int qPow(int b, int e) {
int a = 1;
for (; e; e >>= 1, b = (LL)b * b % Mod)
if (e & 1) a = (LL)a * b % Mod;
return a;
}
int N, A[MN], B[MN];
int Fac[MS * 2], iFac[MS * 2];
int S[MS][MS];
int Ans;
int main() {
scanf("%d", &N);
Fac[0] = 1;
for (int i = 1; i <= 4 * C; ++i) Fac[i] = (LL)Fac[i - 1] * i % Mod;
iFac[4 * C] = qPow(Fac[4 * C], Mod - 2);
for (int i = 4 * C; i >= 1; --i) iFac[i - 1] = (LL)iFac[i] * i % Mod;
for (int i = 1; i <= N; ++i) {
scanf("%d%d", &A[i], &B[i]);
++S[O - A[i]][O - B[i]];
Ans = (Ans - (LL)Fac[2 * (A[i] + B[i])] * iFac[2 * A[i]] % Mod * iFac[2 * B[i]]) % Mod;
}
for (int i = O - C; i <= O + C; ++i)
for (int j = O - C; j <= O + C; ++j)
S[i][j] = (S[i][j] + S[i - 1][j] + S[i][j - 1]) % Mod;
for (int i = 1; i <= N; ++i)
Ans = (Ans + S[O + A[i]][O + B[i]]) % Mod;
Ans = (LL)Ans * Inv2 % Mod;
printf("%d\n", (Ans + Mod) % Mod);
return 0;
}
F - Wide Swap
详细题解请见:AtCoder Grand Contest 001 F: Wide Swap。
#include <cstdio>
#include <algorithm>
#include <queue>
const int Inf = 0x3f3f3f3f;
const int MN = 500005, MS = 1 << 20 | 7;
int N, K, P[MN], Ans[MN];
#define li (i << 1)
#define ri (li | 1)
#define mid ((l + r) >> 1)
#define ls li, l, mid
#define rs ri, mid + 1, r
int mxp[MS];
void Build(int i, int l, int r) {
if (l == r) return mxp[i] = l, void();
Build(ls), Build(rs);
mxp[i] = P[mxp[li]] > P[mxp[ri]] ? mxp[li] : mxp[ri];
}
void Del(int i, int l, int r, int p) {
if (l == r) return mxp[i] = 0, void();
p <= mid ? Del(ls, p) : Del(rs, p);
mxp[i] = P[mxp[li]] > P[mxp[ri]] ? mxp[li] : mxp[ri];
}
int Qur(int i, int l, int r, int a, int b) {
if (r < a || b < l) return 0;
if (a <= l && r <= b) return mxp[i];
int v1 = Qur(ls, a, b), v2 = Qur(rs, a, b);
return P[v1] > P[v2] ? v1 : v2;
}
int inq[MN];
std::priority_queue<int> pq;
inline void check(int id) {
if (inq[id]) return ;
if (Qur(1, 1, N, id - K + 1, id + K - 1) == id)
pq.push(id), inq[id] = 1;
}
int main() {
scanf("%d%d", &N, &K);
for (int i = 1; i <= N; ++i) scanf("%d", &P[i]);
P[0] = -Inf;
Build(1, 1, N);
for (int i = 1; i <= N; ++i) check(i);
for (int i = N; i >= 1; --i) {
int u = pq.top(); pq.pop();
Ans[u] = i;
Del(1, 1, N, u);
int pos;
if ((pos = Qur(1, 1, N, u - K + 1, u - 1))) check(pos);
if ((pos = Qur(1, 1, N, u + 1, u + K - 1))) check(pos);
}
for (int i = 1; i <= N; ++i) printf("%d\n", Ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号