[算法学习记录] 并查集（附例题）

并查集简介

并查集是一种重要的数据结构，主要用于实现节点之间的合并查询操作（例如判断两个节点是否属于同一个连通块（共享同一个父节点的节点组成的集合叫连通块）），在解决不相交集合时有很大的用处；并查集同样常用于处理无向图，来描述接点的连通性，在初始化时，每个节点默认指向自己；
在并查集中，每一个节点有且仅有一个父节点（我喜欢称它为根）。

并查集的实现

1. 寻找父节点
   我们可以通过递归的方式一路向上寻找，直到找到父节点，示例代码：

int root(int x)
{
	return pre[x] == x ? x : root(pre[x]);
}

这种方法有一种缺陷，如果节点连接成一条长链，那么每次查找父节点时，时间复杂度均为O(n),显然，如果数据量稍微大一点，时间复杂度也会变得非常大，为了改善时间复杂度我们可以对并查集进行路径压缩，使每个节点直接指向父节点，而不是每次都重新查询，这样均摊下来每次查询的复杂度就会接近O(1),图例及代码如下：

路径压缩前

路径压缩后

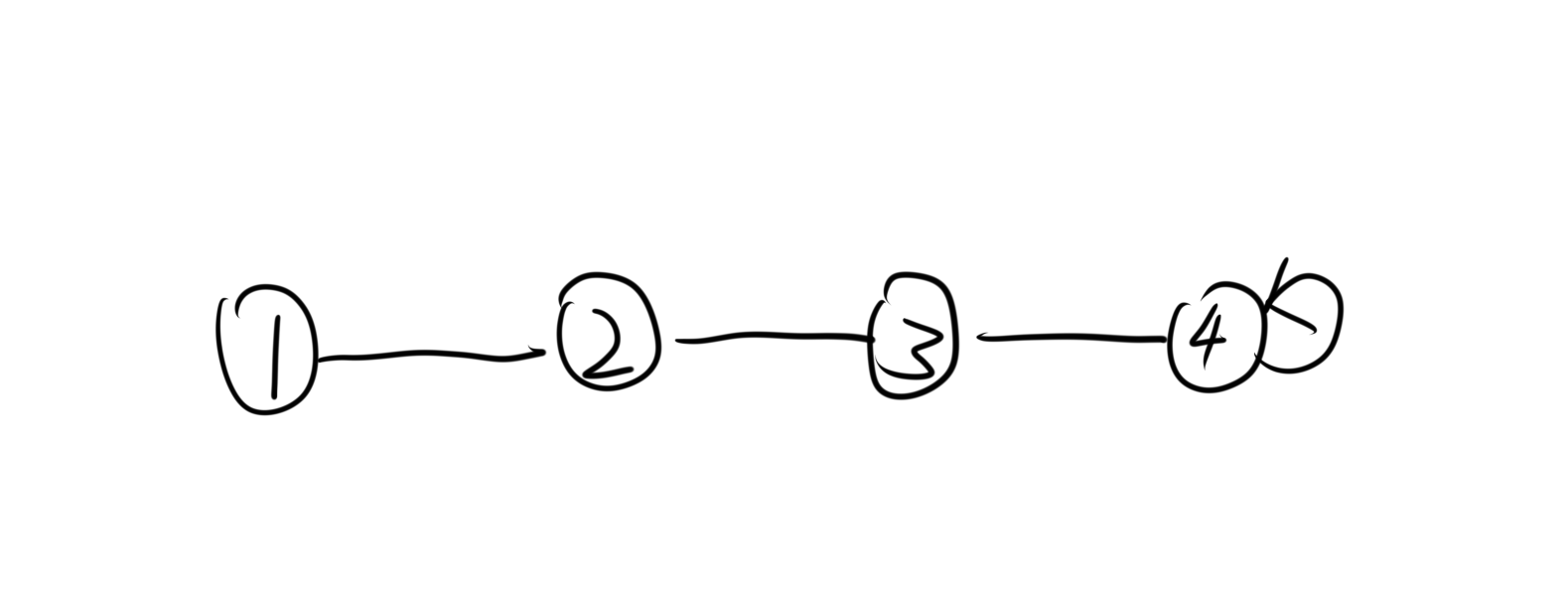
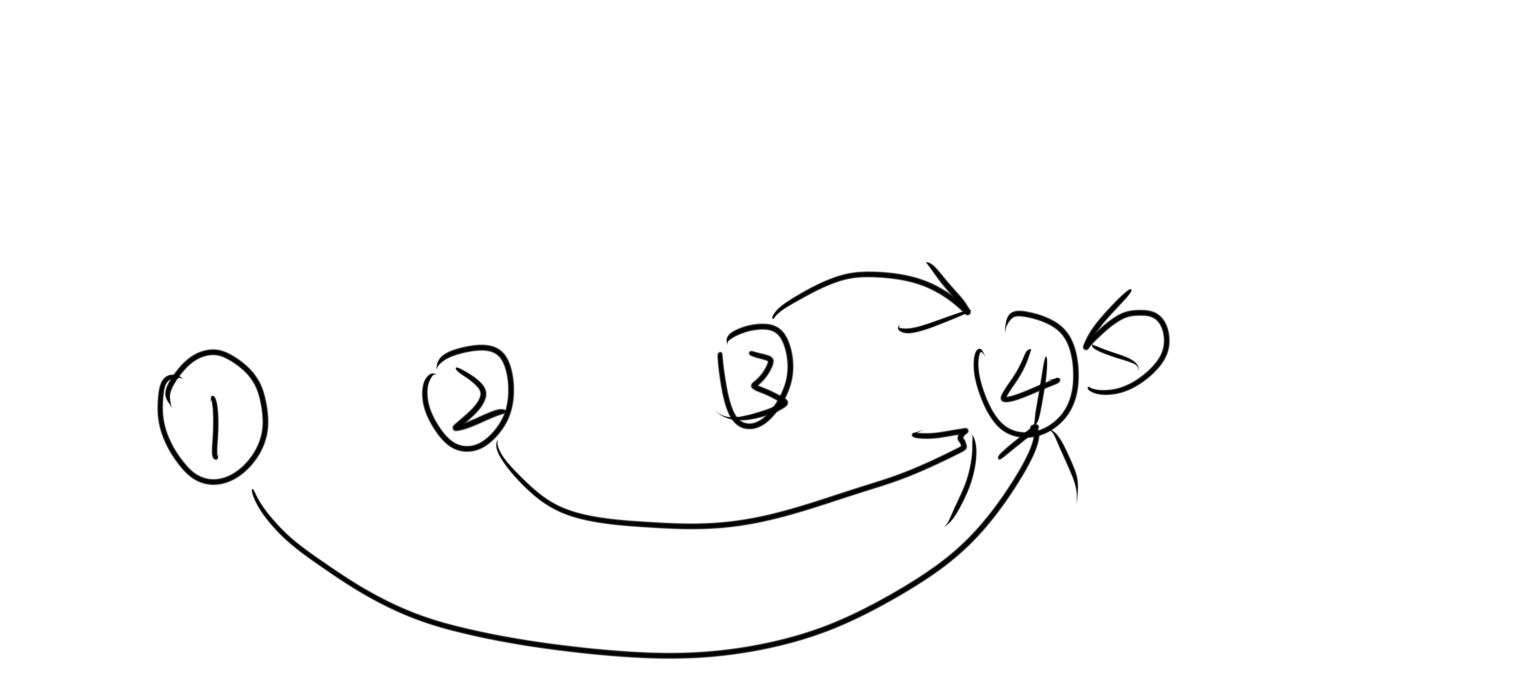
2. 节点的连接
   在初始状态下，各个节点的父节点都是它本身，我们需要根据题目给出的数据对节点所在的集合进行连接，只要我们把它们的父节点相连，就可以实现两集合的连接，代码实现如下：

void merge(int x, int y)
{
    pre[root(x)] = root(y);
    //当然pre[root(y)] = root(x);也是可以的
}

例题

星码 P68 联通块问题
我们已经知道联通块就是公用一个父节点的点的集合，而并查集就是用来解决这种问题的，我们可以把每个节点都存到并查集里面，在对它们进行遍历只要出现一个父节点sz[root(i)]就+1（sz数组是记录个集合大小的数组），之后可以创建一个数组v，在对sz进行遍历，为避免重复，只有root(i)=i时才把联通块大小放入数组v中，完成以上操作后，输出数组v即可。代码如下：

#include<bits/stdc++.h>
using namespace std;
using ll = long long;

const int N = 2e5 + 5;
int pre[N], sz[N];
//pre数组存储的的是每个节点的指向，sz数组存储的是每个集合的大小（根相同的点组成连通块）

int root(int x)
{
	return pre[x] = (pre[x] == x ? x : root(pre[x]));
}
//寻找根节点的函数（采用了路径压缩，每个点直接指向他的根）
/*
不采用路径压缩(本题数据量较大，会超时)
int root(int x)
{
	return pre[x] == x ? x : root(pre[x]);
}
*/

void solve()
{
	int n, m; cin >> n >> m;

	for (int i = 1; i <= n; i++) pre[i] = i;
	//并查集默认初始化为指向自己
	while (m--)
	{
		int x, y; cin >> x >> y;
		pre[root(x)] = root(y);
	}
	//x，y间存在无向边，说明两点连结将两者的根相连即代表两节点相连
	vector<int> v;
	//存储连通块的大小
	for (int i = 1; i <= n; i++) sz[root(i)]++;
	//统计连通块大小（跟相同即为同一个连通块）
	for (int i = 1; i <= n; i++) if (root(i) == i) v.push_back(sz[i]);
	//找到根节点，记录连通块大小
	sort(v.begin(), v.end());
	//从小到大排序
	for (const auto &val : v) cout << val << " ";
	//输出
}

int main()
{
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	int _ = 1;
	while (_--) solve();
	return 0;
}

本人初学算法，文章难免有纰漏，如有错误，敬请指正。