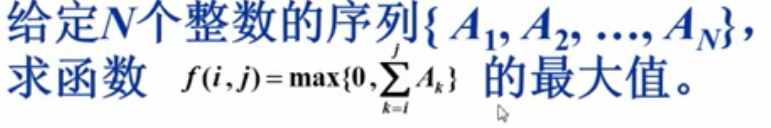
这里摘自慕课浙大陈越姥姥的课程问题

介绍对于一个问题，以不通的算法来计算的效率比较。

首先我们使用算法一：暴力算法

int MaxSubseqSum1(int A[],int N)
{
    int Thissum,MaxSum = 0;
    int i,j,k;
    for ( i= 0;i<N;i++)   /* i是子列左端位置 */ 
    {
        for(j=i;j<N;j++)    /* j 是子列右端位置 */ 
        {
            Thissum = 0;  /*Thissum是A[i]到A[j]的子列和*/ 
            for(k = i;k<=j;k++)  
                Thissum += A[k];
            if(Thissum >MaxSum)
                MaxSum = Thissum;
        }
    }
    return MaxSum; 
}

额。。。这个算法的时间复杂度为 O(N^3)貌似对于处理一些大型数据程序会被中断。我们尝试将时间复杂度降低。

由此来到算法二

int MaxSubseqSum2(int A[],int N)
{
    int Thissum,MaxSum = 0;
    int i,j,k;
    for ( i= 0;i<N;i++)   /* i是子列左端位置 */ 
    {
        for(j=i;j<N;j++)    /* j 是子列右端位置 */ 
        {
            Thissum = Thissum + A[j];
            if(Thissum >MaxSum)
                MaxSum = Thissum;
        }
    }
    return MaxSum; 
}

这里算法使用递加替换了k的for循环，使时间复杂度为O(N^2)

呃。。一个专业的程序猿会将 时间复杂度为 n^2的算法转换为 N*log N

呢么这里我们就请出重点人物，分而治之

int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}

int DivideAndConquer( int List[], int left, int right )
{ 
/* 分治法求List[left]到List[right]的最大子列和 */    
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */    
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/     
    int LeftBorderSum, RightBorderSum;    
    int center, i;     
    if( left == right )  
    { 
    /* 递归的终止条件，子列只有1个数字 */        
        if( List[left] > 0 )  
            return List[left];        
        else 
            return 0;    
    }     
    /* 下面是"分"的过程 */    
    center = ( left + right ) / 2; /* 找到中分点 */    
    /* 递归求得两边子列的最大和 */    
    MaxLeftSum = DivideAndConquer( List, left, center );    
    MaxRightSum = DivideAndConquer( List, center+1, right );     
    /* 下面求跨分界线的最大子列和 */    
    MaxLeftBorderSum = 0; LeftBorderSum = 0;    
    for( i=center; i>=left; i-- ) 
    { 
        /* 从中线向左扫描 */        
        LeftBorderSum += List[i];        
        if( LeftBorderSum > MaxLeftBorderSum )            
            MaxLeftBorderSum = LeftBorderSum;    
    } /* 左边扫描结束 */     
    MaxRightBorderSum = 0; RightBorderSum = 0;    
    for( i=center+1; i<=right; i++ ) 
    { 
        /* 从中线向右扫描 */        
        RightBorderSum += List[i];        
        if( RightBorderSum > MaxRightBorderSum )            
            MaxRightBorderSum = RightBorderSum;    
    } /* 右边扫描结束 */     
    /* 下面返回"治"的结果 */    
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
} 
int MaxSubseqSum3( int A[], int N )
{ 
    /* 保持与前2种算法相同的函数接口 */    
    return DivideAndConquer( A, 0, N-1 );
}

首先我们来分析一下这段代码，一个 比较大小Max3函数，没有问题，第三个保持和前面算法接口相同的函数没有问题，重点在第二个函数我们要理解这段代码我们首先要理解分而治之的思想，

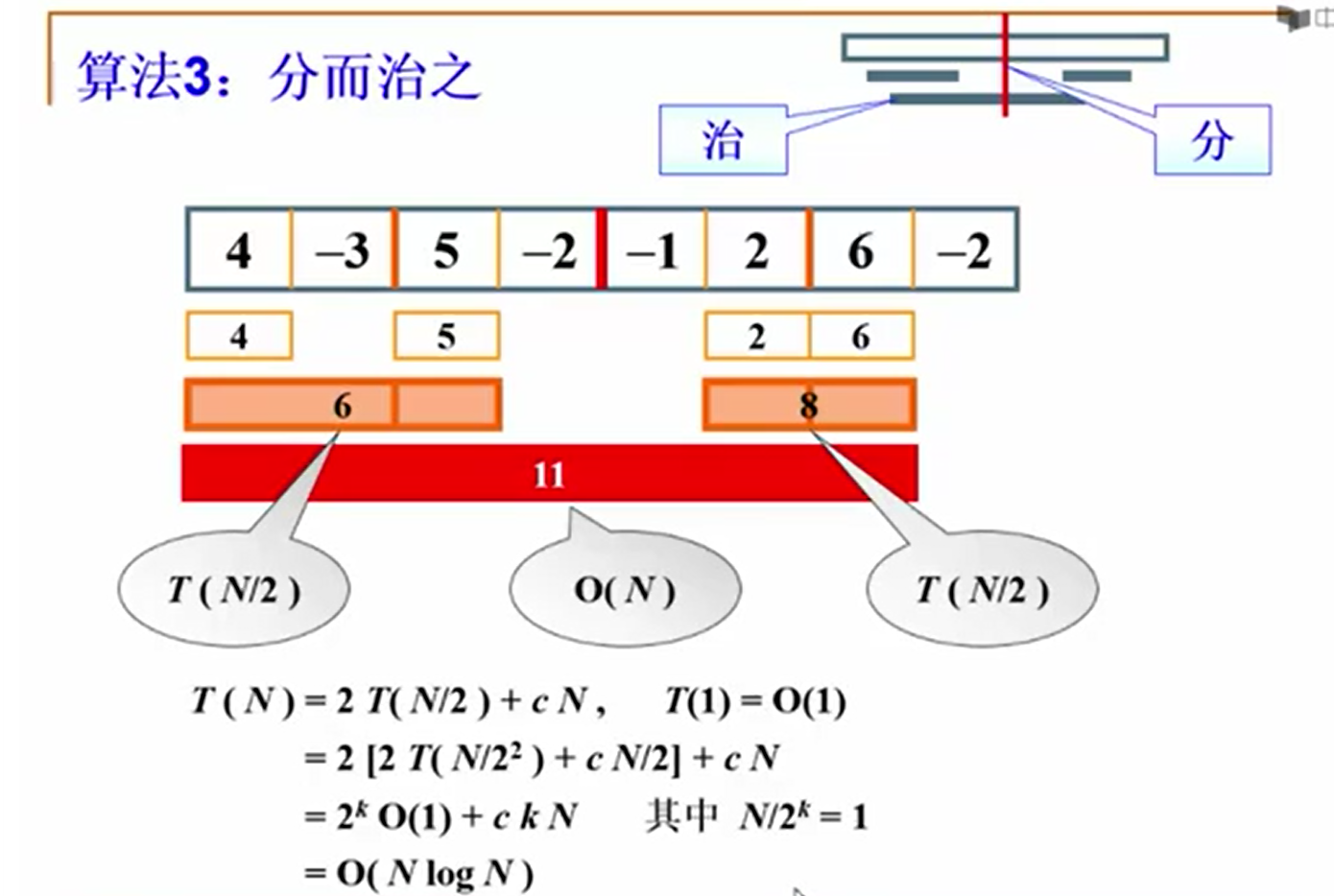如图，给出一个数组含有8个元素，将之一分为二，递归调用分分分分，分成最后只有一个 4 | -3，4在 | 中算最大，-3<0即为0，这是分，然后我们看  4 | -3的治，从   |   开始  分别向左和右走(加)，明显结果为  1，呢么治为  1 ，  1和  0  和  4相比较得出  ，4最大，再举一个   我们看  4  -3 | 5 -2   注意  | 的位置，由分 得出左半边  最大为  4，右半边最大为5，我们看治，从  | 开始  向左右两边加  ，得出  治  为  4 + -3 +5 = 6.  

最后一种方法为在线处理  时间复杂度为  O (N)

int MaxSubseqSum4(int A[], int N)
{
    int Thissum,MaxSum;
    int i;
    Thissum = MaxSum =0;
    for(i=0;i<N;i++)
    {
        Thissum += A[i]; /*向右累加*/ 
        if(Thissum>MaxSum)
            MaxSum = ThisSum;//发现更大和则更新当前结果 
        else if(Thissum<0) //如果为负数则 
            Thissum = 0;
    }
    return MsxSum;
}
     } 
}

这里我们分析这个数组，  从  -1  开始  小于  0呢么  直接跳过  从 3开始  3 -2 = 1>0并令MaxSum = 1没有问题， 1+4 =5 >0没有问题，5-6 <0  呢么跳过从  -6后面的1开始1+6 =7 ，MaxSum = 7

 

个人总结，对于一个问题来讲，我们程序员能解决的情况下，可以将它的时间复杂度  降低到  O(N*logN)甚至 O(N)  会大大提高算法的效率。