CS229：局部加权回归与逻辑斯谛回归

当数据的规律不能很好的用直线拟合，我们使用局部加权回归来处理各种其他拟合方式。

参数学习与非参数学习

参数学习：参数是固定的，只需要通过学习确定即可

非参数学习：参数不确定，需要保持改变，通常参数数目与数据规模线性相关。（对大规模数据不太友好）

对某个训练集提出假设的方式：

线性回归：使θ适应为成本函数最小的参数值。成本函数中所有训练集的权值相同。

局部加权回归：集中注意力在预测点周围的训练集，而对其他值给予较小的权值。性质数较少。

修正成本函数为：

 

 

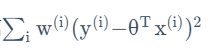
其中wⁱ是每个训练组的权重，由此公式给出：

 

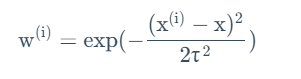
可以看出，离当前预测值越近的训练组，具有越高的权值。最远的则接近于0。其中的τ是带宽，影响着选取主要数据的宽度。

 

 使用平方误差的原因：概率解释

假设目标变量取值和输入值之间存在如下等量关系：

 

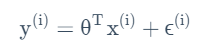
其中的ε代表随机误差向量，服从以下规律：

 

 

 

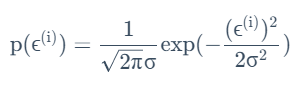
 从而意味着存在如下等量关系：

 

 

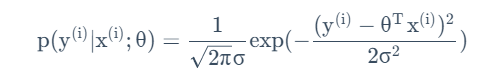
 其中θ是参数，但不是随机变量。当我们将θ视为自变量时，这一等量关系将被称为一个似然函数，描述的是对xi，yi的某种给定分布，参数取值的可能。改写为如下形式：

 

 

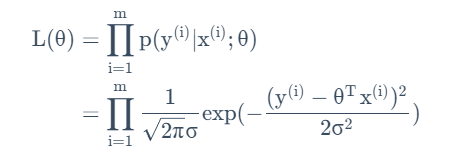
 根据极大似然法，我们只需要通过类似求导的方法来找到最有可能的参数取值，便证明了这一参数是最有可能取得的，自然是与事实情况符合的最好的，与成本函数的初衷不谋而合。对上述函数的对数求导得，对该函数取得最大值即等价为原成本函数取最小值。

 

 

 从而给出了选择最小二乘法的原因。

分类问题：线性回归表现不好，决策边界很容易受某些极端训练数据影响。

逻辑回归：改变假设函数的形式：

 

 

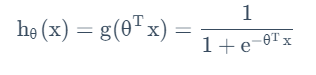
 这个函数叫做逻辑函数（Logistic Function）

 

 

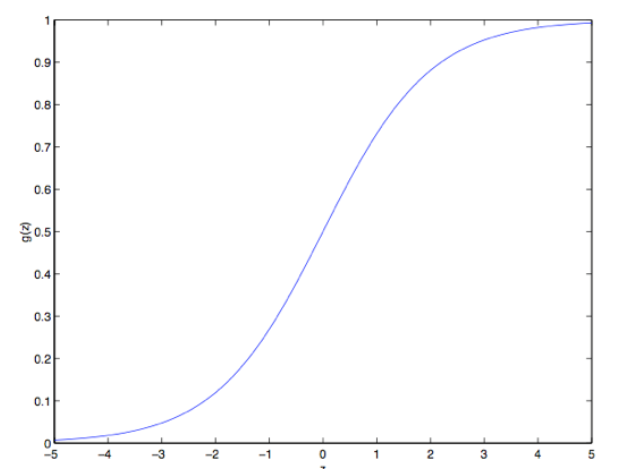
 它的导数具有如下性质：

 

 

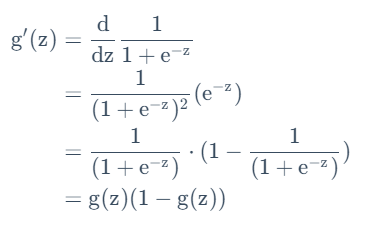
 同样采取最大似然法推成本函数

根据0-1分布和取对数得：

 

 

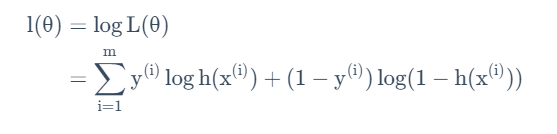
 以此作为成本函数。不同的是，此时希望使该函数值最大，为此我们应用梯度上升法，对该函数求偏导来确定更新规则：

 

 

 从而得到的更新规则为：

 

 

 

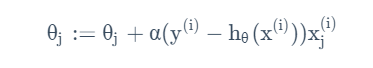
可以看出来，形式与LMS方法中的更新模式是类似的，只不过假设的形式不同。实际上，对这种无局部最优，有统一思路为广义线性回归。

逻辑回归没有法方程。

牛顿法：寻找方程根（在此处即一阶导数为0，即取得成本函数 最大值）

在预测点求切线，迭代为切线和横轴的交点。

 

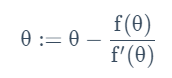
精度值二次收敛，故而结果十分迅速。

但是在过高维度的问题中，牛顿法的矩阵开销将会变得非常巨大。