2019-08-21 纪中NOIP模拟A组
T1 [JZOJ6315] 数字
题目描述

数据范围

分析
我叕正解写挂了,写模拟一定要仔细考虑细节啊
正解是这样说的

我是在 $n$ 串中按位数从小到大枚举数字匹配,思路和正解相似,时间复杂度相同,做法稍有不同

#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #include <vector> #include <queue> using namespace std; #define ll long long ll inf = 1e18, p[20] = {1}; int t, n, a[20]; char s[20]; ll solve() { for (int i = 1; i <= n; i++) { ll ans = inf; for (int j = 1; j <= i; j++) { if (!a[j]) continue; ll now = 0; int len = i, k = j + i, f = 0; for (int l = 0; l < i; l++) { if (j + l <= n) now = now * 10 + a[j + l]; else now = now * 10 + a[j + l - i]; } if (j + i - 1 > n) { ll last = now % p[j + i - 1 - n]; now = now - last + (last + 1) % p[j + i - 1 - n]; } for (int l = 1; j - l; l++) if (a[j - l] != (now - 1) / p[l - 1] % 10) {f = 1; break;} if (f) continue; if (++now / p[len]) len++; while (k + len - 1 <= n) { for (int l = 0; l < len; l++) if (a[k + l] != now / p[len - l - 1] % 10) {f = 1; break;} if (f) break; k += len; if (++now / p[len]) len++; } if (f) continue; if (k > n) now--; else { for (int l = 0; k + l <= n; l++) if (a[k + l] != now / p[len - l - 1] % 10) {f = 1; break;} if (f) continue; } ans = min(ans, now); } if (ans < inf) return ans; } } int main() { scanf("%d", &t); for (int i = 1; i <= 18; i++) p[i] = p[i - 1] * 10; while (t--) { scanf("%s", s + 1); n = strlen(s + 1); for (int i = 1; i <= n; i++) a[i] = s[i] - '0'; printf("%lld\n", solve()); } return 0; }
T2 [JZOJ6313] Maja
题目描述
蜜蜂 $Maja$ 到了一片草地,草地可以被描述成 $N$ 行 $M$ 列的网格图,在第 $i$ 行第 $j$ 列的位置上有 $C_{i,j}$ 朵未授粉的花。
$Maja$ 会从第 $A$ 行第 $B$ 列出发,每次只能移动到与当前位置四相邻的格子上,且不能移动到草地以外。每到达一个格子,她会把此处所有未授粉的花都授粉。
然而,当 $Maja$ 离开一个格子,此处又会长出 $C_{i,j}$ 朵未授粉的花。
$Maja$ 想知道,如果她从第 $A$ 行第 $B$ 列出发,选择一条长度恰好为 $K$ 的路径,最后又回到第 $A$ 行第 $B$ 列,最多能为多少朵花授粉。
数据范围
对于 $40\%$ 的数据,$K \leq 10^4$
对于 $100\%$ 的数据,$2 \leq N,M \leq 100$,$2 \leq K \leq 10^9$
分析
很容易发现,最优路径是先走到某个点处开始绕环走,最后再原路回到起点
又很容易发现,最优情况下环上只有两个点
设 $f[i][j][k]$ 表示经过 $k$ 步走到点 $(i,j)$ 处时的最大点权和
对于每个 $f$ 值,可以在点 $(i,j)$ 与其四相邻中点权最大的点上来回走,求出该情况下的最优值
观察可知 $k$ 值最大为 $min(n \times m, \frac{k}{2})$,但空间复杂度仍无法承受,因此需要滚动数组

#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #include <vector> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 101 int n, m, a, b, t; ll ans, g[N][N], h[N][N], f[N][N][2]; int d[4][2] = {0, 1, 1, 0, 0, -1, -1, 0}; bool check(int x, int y) { if (x < 1 || x > n) return false; if (y < 1 || y > m) return false; return true; } int main() { scanf("%d%d%d%d%d", &n, &m, &a, &b, &t); for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) scanf("%lld", &g[i][j]); for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) for (int k = 0; k < 4; k++) { int x = i + d[k][0], y = j + d[k][1]; if (!check(x, y)) continue; h[i][j] = max(h[i][j], g[i][j] + g[x][y]); } int limit = min(n * m, t / 2); memset(f, -1, sizeof f); f[a][b][0] = 0; for (int k = 0; k <= limit; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) { for (int l = 0; l < 4; l++) { int x = i + d[l][0], y = j + d[l][1]; if (!check(x, y) || f[x][y][(k & 1) ^ 1] == -1) continue; f[i][j][k & 1] = max(f[i][j][k & 1], f[x][y][(k & 1) ^ 1] + g[i][j]); } if (f[i][j][k & 1] == -1) continue; ans = max(ans, f[i][j][k & 1] * 2 + (t / 2 - k) * h[i][j] - g[i][j]); } printf("%lld", ans); return 0; }
T3 [JZOJ6316] djq的朋友圈
题目描述

数据范围

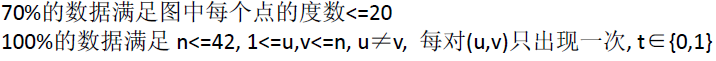
分析
前面的 $70 \, pts$ 用状压 $dp$ 是能够想到的,先状压处理出通过 $1$ 的每个熟人,使得 $1$ 的所有非熟人是否能确立与 $1$ 关系,是否与 $1$ 为盟友,然后对已排列的熟人的集合的状态进行转移
我们观察发现,当 $1$ 的熟人个数大于 $20$ 时,$1$ 的非熟人个数一定小于等于 $20$,所以只需要把状态改为已确立关系的非熟人的集合,用相似的方法转移

#include <iostream> #include <cstdio> #include <cstdlib> #include <cstring> #include <algorithm> #include <vector> #include <queue> using namespace std; #define ll long long #define inf 0x3f3f3f3f #define N 44 #define M 1 << (N >> 1) int n, m, cnt1, cnt2, ans; int g[N][N], f[M], num[N]; ll vis[N], rel[N]; int Cnt(ll s) { int sum = 0; while (s) s &= (s - 1), sum++; return sum; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= m; i++) { int u, v, w; scanf("%d%d%d", &u, &v, &w); if (w) g[u][v] = g[v][u] = -1; else g[u][v] = g[v][u] = 1; } for (int i = 2; i <= n; i++) if (g[1][i]) { num[i] = ++cnt1; if (g[1][i] > 0) ans++; for (int j = 2; j <= n; j++) if (!g[1][j] && g[i][j]) { if (!num[j]) num[j] = ++cnt2; vis[num[i]] |= (1ll << num[j] - 1); if (g[1][i] * g[i][j] > 0) rel[num[i]] |= (1ll << num[j] - 1); } } memset(f, -1, sizeof f); f[0] = 0; if (cnt1 <= 20) { for (int i = 0; i < (1 << cnt1); i++) if (f[i] >= 0) { ll now = 0; for (int j = 1; j <= cnt1; j++) if (i & (1 << j - 1)) now |= vis[j]; for (int j = 1, k; j <= cnt1; j++) if ((k = i | (1 << j - 1)) != i) f[k] = max(f[k], f[i] + Cnt(rel[j] & (~now))); } ans += f[(1 << cnt1) - 1]; } else { for (int i = 0; i < (1 << cnt2); i++) if (f[i] >= 0) for (int j = 1, k; j <= cnt1; j++) if ((k = i | vis[j]) != i) f[k] = max(f[k], f[i] + Cnt(rel[j] & (~i))); ans += f[(1 << cnt2) - 1]; } printf("%d", ans); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号