『初赛常考考点复习』

时间复杂度

渐进符号

用\(\Theta(f(n))\)表示函数\(f(n)\)的渐进上下界，\(O(f(n))\)表示函数\(f(n)\)的渐进上界，\(\Omega(f(n))\)表示函数\(f(n)\)的渐进下界。

其含义是，存在确定的常数\(n_0,c_1,c_2\)，当\(n\geq n_0\)时，都满足：

\[c_1f(n)\leq \Theta(f(n))\leq c_2f(n),\ O(f(n))\leq c_2f(n),\ c_1f(n)\leq \Omega(f(n)) \]

势能分析法

首先，我们可以假设总共有\(m\)次操作，每次操作的实际消耗时间\(t_i\)难以估计，那么我们可以引入一个势能\(\Phi_i\)表示第\(i\)次操作完后的某个特征值，然后用\(a_i=t_i+\Delta\Phi=t_i+\Phi_i-\Phi_{i-1}\)表示第\(i\)次操作的均摊时间，那么有：

\[\sum_{i=1}^m t_i=\sum_{i=1}^m(a_i-\Delta \Phi)=\sum_{i=1}^m a_i+\Phi_0-\Phi_m \]

那么就可以通过分析\(\sum_{i=1}^m a_i+\Phi_0-\Phi_m\)的大小来分析\(m\)次操作的总时间。

分治时间分析：解递归式

Master Theorem

对于递归式\(T(n)=aT\left(\dfrac{n}{b}\right)+f(n),\forall n\geq b\)，若在\(n< b\)时\(T(n)=\Theta(1)\)，则：

\[T(n)= \begin{cases} \Theta\left(n^{\log_b a}\right), & f(n)=O\left(n^{\log_b a-\epsilon}\right) \\ \Theta(f(n)), & f(n)=\Omega\left(n^{\log_b a+\epsilon}\right) \\ \Theta\left(n^{\log_b a}\log^{k+1}n\right), &f(n)=\Theta\left(n^{\log_b a}\log ^k n\right),k\geq 0 \end{cases} \]

Akra-Bazzi Theorem

对于递归式\(T(n)=\displaystyle\sum_\limits{i=1}^{k}a_iT\left(\dfrac{n}{b_i}\right)+f(n),\forall n\geq b\)，若在\(n< b\)时\(T(n)=\Theta(1)\)，则：

\[T(n)=\Theta\left( n^p\left( 1+\int_{1}^n \frac{f(x)}{x^{p+1}}\text d x \right) \right), \text{where} \sum_{i=1}^k\frac{a_i}{b_i^p}=1 \]

例如：

\(T(n)=3T\left(\dfrac{n}{2}\right)+4T\left( \dfrac{n}{4} \right)+n\)，找到\(p=2\)，那么\(T(n)=\Theta\left( n^2\left(1+\displaystyle\int_1^n \dfrac{\text d x}{x^2}\right) \right)=\Theta(n^2)\)。

\(T(n)=2T\left(\dfrac{n}{2}\right)+\log n\)，找到\(p=1\)，那么\(T(n)=\Theta\left( n\left(1+ \displaystyle\int_1^n \dfrac{\log x}{x^2} \text dx \right) \right)=\Theta(n-\log n)=\Theta(n)\)。

\(\displaystyle \int\frac{\ln x}{x^2}\text d x\)可以用分部积分公式：\(\displaystyle \int u\text d v=uv-\displaystyle \int v\text d u\)：

\[\text{let}\ u = \ln x,\text d v=\frac{\text d x}{x^2}\Rightarrow v=\int x^{-2}\text d x=-x^{-1} \\ \begin{aligned} \\ \int\frac{\ln x}{x^2}\text dx & = -x^{-1}\ln x+\int x^{-1}\text d(\ln x) \\ & = -\frac{\ln x}{x}+\int x^{-2}\text d x = -\frac{\ln x+1}{x} \end{aligned} \]

\(T(n)=2T\left( \dfrac{n}{2} \right)+\dfrac{n}{\log n}\)，找到\(p=1\)，那么\(T(n)=\Theta\left(n\left( 1+\displaystyle \int _1^n \dfrac{\text d x}{x\log x} \right)\right)=\Theta(n+n\log \log n)=\Theta(n\log \log n)\)。

\(\displaystyle \int \dfrac{\text d x}{x \log x}\)可以用换元积分方法：

\[\text{let } u=\log x\Rightarrow \text d u = \frac{\text d x}{x},\text dx=x\text d u \\ \begin{aligned} \int \dfrac{\text d x}{x \log x} & = \int \frac{x\text d u}{xu}=\int \frac{\text du}{u}=\log u = \log\log x \end{aligned} \]

递归树方法

\(1.\) 解递归式\(T(n)=\sqrt n\times T(\sqrt n)+n\)，\(n\)足够小时\(T(n)=1\)。

\(\text{Solution}:\) 显然递归树的每一层的总大小为\(O(n)\)，且每次递归数字的位数减半，数字有\(\lg n\)位，那么递归树深度就是\(\log_2 \lg n\)，故\(T(n)=O(n\log_2 \lg n)\)。

\(2.\) 解递归式\(T(n)=4\sqrt n\times T(\sqrt n)+n\)，\(n\)足够小时\(T(n)=1\)。

\(\text{Solution}:\) 不妨设\(f(x)\)表示递归树第\(x\)层的节点大小，\(g(x)\)表示递归树第\(x\)层的节点数量，列出递推方程：

\[\begin{cases} f(x)=\sqrt {f(x-1)}, & f(0)=n \\ g(x)=g(x-1)\times 4\sqrt{f(x-1)}, & g(0)=1 \end{cases} \]

显然\(f(x)=n^{2^{-x}}\)，那么

\[g(x)=g(x-1)4n^{2^{-x}}=\prod_{i=1}^x4n^{2^{-i}}=4^xn^{\sum_{i=1}^x 2^{-i}}=4^xn^{1-2^{-x}} \]

设\(S(x)\)表示递归树第\(x\)层的时间总消耗，显然\(S(x)=f(x)g(x)=n\times 4^x\)，所以：

\[T(n)=\sum_{i=0}^{\log_2 \lg n}S(i)=n \sum_{i=0}^{\log _2 \lg n}4^i =O\left(n \left(2^{\log_2 \lg n}\right)^2 \right)=O\left( n\lg^2 n \right) \]

算法和问题复杂性

问题：对于一个包含由\(0\)和\(1\)组成的字符串集合\(S\)，以某个\(01\)字符串\(x\)作为输入，要求某个图灵机判断\(x\)在不在\(S\)里面。这里的图灵机可以先想象成平时我们用的计算机，\(S\)也可以被看成我们要解决的问题。注意我们的问题非常简单，就是要判断某个字符串\(x\)是否在某个集合\(S\)里面，下面是定义：

• \(\text P\)类问题：有一个图灵机在多项式时间内能够判断\(x\)是否在\(S\)里面。
• \(\text{NP}\)：有一个图灵机\(M\)，如果某个字符串\(x\)在\(S\)里面，那么存在一个验证字符串\(u\)（注意这个\(u\)是针对这个\(x\)的，而且长度必须是\(x\)长度的多项式\(|u|=|x|^c\)关系)，\(M\)以\(x\)和\(u\)作为输入，能够验证\(x\)真的是在\(S\)里面。
• \(\text{NP-hard}\)：如果某个问题\(S\)是\(\text{NP-hard}\)，那么对于任意一个\(\text{NP}\)问题，我们都可以把这个\(\text{NP}\)问题在多项式时间之内转化为\(S\)，并且原问题的答案和转化后\(S\)的答案是相同的。也就是说只要我们解决了\(S\)，那么就解决了所有的\(\text{NP}\)问题。
• \(\text{NP-complete}\)：一个问题既是\(\text {NP-hard}\)，又是\(\text{NP}\)问题。

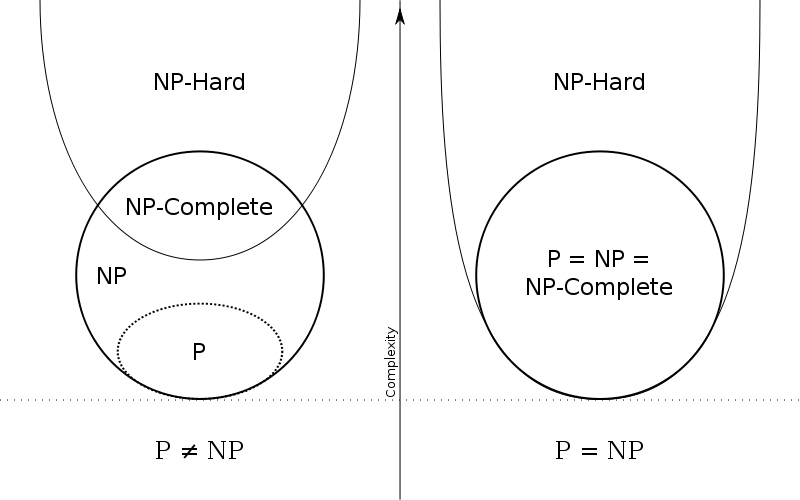
• 对问题复杂性的讨论基于问题的性质：求解性问题，而非计数\(/\)构造等其他问题。
• \(\text{NP}\)问题的定义为对于一个证据\(u\)可以在多项式时间内验证，\(\text P\)为\(\text{NP}\)的子集，不能说所有\(\text{NP}\)问题都不确定是否存在多项式时间的算法，因为\(\text P\)问题也是\(\text {NP}\)问题，已经确定存在多项式时间的算法。

全国青少年信息学奥林匹克竞赛系列活动简介

背景

\(1984\)年*指出：“计算机的普及要从娃娃做起。”中国计算机学会于\(1984\)年创办全国青少年计算机程序设计竞赛（即\(\text{NOI}\)），当年参加竞赛的有\(8000\)多人。这一新的活动形式受到党和政府的关怀，得到社会各界的关注与支持。中央领导王震同志出席了首届竞赛发奖大会，并对此项活动给予了充分肯定。

各活动及其简介

\(\text{NOI}\)系列活动包括：全国青少年信息学奥林匹克竞赛和全国青少年信息学奥林匹克网上同步赛、全国青少年信息学奥林匹克联赛、冬令营、选拔赛和出国参加\(\text{IOI}\)。

\(\text{NOI}\)：全国青少年信息学奥林匹克（\(\text{NOI}\)）是国内包括港澳在内的省级代表队最高水平的大赛，自\(1984\)年至今，在国内包括香港、澳门组织竞赛活动。每年经各省选拔产生\(5\)名选手（其中一名是女选手），由中国计算机学会在计算机普及较好的城市组织进行比赛。这一竞赛记个人成绩，同时记团体总分。

\(\text{NOI}\)期间，举办同步夏令营和\(\text{NOI}\)网上同步赛，给那些程序设计爱好者和高手提供机会。为增加竞赛的竞争性、对抗性和趣味性以及可视化，\(\text{NOI}\)组织进行团体对抗赛，团体对抗赛实质上是程序对抗赛，其成绩纳入总分计算。

\(\text{NOIP}\)：全国青少年信息学奥林匹克联赛(\(\text{National Olympiad in Informatics in Provinces}\)简称\(\text{NOIP}\))自\(1995\)年至今。每年由中国计算机学会统一组织。\(\text{NOIP}\)在 同一时间、不同地点以各省市为单位由特派员组织。全国统一大纲、统一试卷。初、高中或其他中等专业学校的学生可报名参加联赛。联赛分初赛和复赛两个阶段。初赛考察通用和实用的计算机科学知识，以笔试为主。复赛为程序设计，须在计算机上调试完成。参加初赛者须达到一定分数线后才有资格参加复赛。联赛分普及组和提高组两个组别，难度不同，分别面向初中和高中阶段的学生。

冬令营：全国青少年信息学奥林匹克冬令营（简称冬令营）自\(1995\)年起。每年在寒假期间开展为期一周的培训活动。冬令营共8天，包括授课、 讲座、讨论、测试等。参加冬令营的营员分正式营员和非正式营员。获得\(\text{NOI}\)前\(20\)名的选手和指导教师为正式营员，非正式营员限量自愿报名参加。在冬令营授课的是著名大学的资深教授及已获得国际金牌学生的指导教师。

\(\text{APIO}\)：亚洲与太平洋地区信息学奥赛（\(\text{Asia Pacific Informatics Olympiad}\)，简称\(\text{APIO}\)）\(2007\)年创建，该竞赛为区域性的网上准同步赛，是亚洲和太平洋地区每年一次的国际性赛事，旨在给青少年提供更多的赛事机会，推动亚太地区的信息学奥林匹克的发展。\(\text{APIO}\)每年\(5\)月举行，由不同的国家轮流主办。每个参赛团参赛选手上限为\(100\)名，其中成绩排在前\(6\)名的选手作为代表该参赛团的正式选手统计成绩。\(\text{APIO}\)中国赛区由中国计算机学会组织参赛，获奖比例将参照\(\text{IOI}\)。

选拔赛：选拔参加国际信息学奥林匹克中国代表队的竞赛（曾经简称\(\text{CTSC}\)，现为\(\text{CTS}\)）。\(\text{IOI}\)的选手是从获\(\text{NOI}\)前\(20\)名选手中选拔出来的，获得前\(4\)名的优胜者代表中国参加国际竞赛。选拔科目包括：\(\text{NOI}\)成绩、冬令营成绩、论文和答辩、平时作业、选拔赛成绩、口试。上述项目加权产生最后成绩。

\(\text {IOI}\)： 出国参加国际信息学奥林匹克竞赛（\(\text{International Olympiad in Informatics}\)，简称\(\text{IOI}\)）。由中国计算机学会组织代表队，代表中国参加国际每年一次的\(\text{IOI}\)。中国是\(\text{IOI}\)创始国之一。\(\text{IOI}2000\)由中国主办，\(\text{CCF}\)承办。出国参赛得到中国科协和国家自然科学基金委的资助。自\(1989\)年开始，我国在\(\text{NOI}\)（网上同步赛\(99\)年开始）、\(\text{NOIP}\)、冬令营、选拔赛的基础上，组织参加国际信息学奥林匹克竞赛。十几年中选拔\(75\)人次参加了\(\text{IOI}\)，累计获金牌\(46\)块、银牌\(17\)块，铜牌\(12\)块。这些选手不仅在国际大赛中有好的表现，而且在现代的信息学科上也大展才华。

\(\text{CSP-J/S}\)：\(\text{CCF}\)非专业级软件能力认证（\(\text{Certified Software Professional Junior/Senior}\)，简称\(\text{CSP-J/S}\)）创办于\(2019\)年，是由\(\text{CCF}\)统一组织的评价计算机非专业人士算法和编程能力的活动。在同一时间、不同地点以各省市为单位由\(\text{CCF}\)授权的省认证组织单位和总负责人组织。全国统一大纲、统一认证题目，任何人均可报名参加。\(\text{CSP-J/S}\)分两个级别进行，分别为\(\text{CSP-J}\)（入门级，\(\text{Junior}\)）和\(\text{CSP-S}\)（提高级，\(\text{Senior}\)），两个级别难度不同，均涉及算法和编程。\(\text{CSP-J/S}\)分第一轮和第二轮两个阶段。第一轮考察通用和实用的计算机科学知识，以笔试为主，部分省市以机试方式认证。第二轮为程序设计，须在计算机上调试完成。第一轮认证成绩优异者进入第二轮认证，第二轮认证结束后，\(\text{CCF}\)将根据\(\text{CSP-J/S}\)各组的认证成绩和给定的分数线，颁发认证证书。\(\text{CSP-J/S}\)成绩优异者，可参加\(\text{NOI}\)省级选拔，省级选拔成绩优异者可参加\(\text{NOI}\)。

C++常见的数据类型

数据类型	占用空间	数据范围
无值型void	\(0\text{ byte}\)	无值域
布尔型bool	\(1\text{ byte}\)	\(\{\text{false,true}\}\)
有符号短整型short [int] /signed short [int]	\(2\text{ byte}\)	\([-2^{15},2^{15})\)
无符号短整型unsigned short [int]	\(2\text{ byte}\)	\([0,2^{16})\)
有符号整型int /signed [int]	\(4\text{ byte}\)	\([-2^{31},2^{31})\)
无符号整型unsigned [int]	\(4\text{ byte}\)	\([0,2^{32})\)
有符号长整型long [int]/signed long [int]	\(4\text{ byte}\)	\([-2^{31},2^{31})\)
无符号长整型unsigned long [int]	\(4\text{ byte}\)	\([0,2^{32})\)
有符号长整型long long/signed long long	\(8\text{ byte}\)	\([-2^{63},2^{63})\)
无符号长整型unsigned long long	\(8\text{ byte}\)	\([0,2^{64})\)
有符号字符型char/signed char	\(1\text{ byte}\)	\([-2^7,2^7)\)
无符号字符型unsigned char	\(1\text{ byte}\)	\([0,2^8)\)
宽字符型wchar_t (unsigned short)	\(2\text{ byte}\)	\([0,2^{16})\)
单精度浮点型float	\(4\text{ byte}\)	\([-3.4\times 10^{-38},3.4\times 10^{38}]\)
双精度浮点型double	\(8\text{ byte}\)	\([-1.7\times 10^{-308},1.7\times 10^{308}]\)

逻辑运算符和C++中的运算符

逻辑运算符

常见的逻辑运算符：\(\land\)，\(\lor\)，\(\lnot\)，\(\oplus\)，其运算优先级为\(\lnot>\and>\oplus>\lor\)。

C++中的运算符

\(\text{C++}\)当中的运算符有\(16\)个优先等级，同一级的运算符按照结合顺序运算。

优先级\(1\)：() [] -> . :: ++ --，结合序：从左到右。

优先级\(2\)：! ~ ++ -- - + * & (type) sizeof，结合序：从右到左。

优先级\(3\)：->* .*，结合序：从左到右。

优先级\(4\)：* / %，结合序：从左到右。

优先级\(5\)：+ -，结合序：从左到右。

优先级\(6\)：>> <<，结合序：从左到右。

优先级\(7\)：< <= > >=，结合序：从左到右。

优先级\(8\)：== !=，结合序：从左到右。

优先级\(9\)：&，结合序：从左到右。

优先级\(10\)：^，结合序：从左到右。

优先级\(11\)：|，结合序：从左到右。

优先级\(12\)：&&，结合序：从左到右。

优先级\(13\)：||，结合序：从左到右。

优先级\(14\)：?:，结合序：从右到左。

优先级\(15\)：= += -= *= /= %= &= |= ^= <<= >>=，结合序：从右到左。

优先级\(16\)：,，结合序：从左到右。

排序算法

排序算法	平均时间复杂度	最差时间复杂度	最好时间复杂度	空间复杂度	稳定性
插入排序	\(O(n^2)\)	\(O(n^2)\)	\(O(n)\)	\(O(n)\)	稳定
选择排序	\(O(n^2)\)	\(O(n^2)\)	\(O(n^2)\)	\(O(n)\)	不稳定
希尔排序	\(O\left(n^{\frac{3}{2}}\right)\)	\(O(n\log^2 n)\)	\(O(n)\)	\(O(n)\)	不稳定
堆排序	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n)\)	不稳定
冒泡排序	\(O(n^2)\)	\(O(n^2)\)	\(O(n)\)	\(O(n)\)	稳定
快速排序	\(O(n\log n)\)	\(O(n^2)\)	\(O(n\log n)\)	\(O(n)\)	不稳定
归并排序	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n\log n)\)	\(O(n)\)	稳定
计数排序	\(O(n+V)\)	\(O(n+V)\)	\(O(n+V)\)	\(O(n+V)\)	稳定
桶排序	\(O(n\log \dfrac{n}{k})\)	\(O(n\log n)\)	\(O(n)\)	\(O(n+k)\)	稳定
基数排序	\(O(n\lg V)\)	\(O(n\lg V)\)	\(O(n\lg V)\)	\(O(10n)\)	稳定

\(\boldsymbol{notes}\)：计数排序为利用值域大小的数组统计排名的排序，桶排序则将数据分\(k\)个组，组内用其他算法排序，当数据分布均匀时\(O\left( n+k\left(\dfrac{n}{k}\log\dfrac{n}{k}\right) \right)\)近似于\(O(n)\)，此时空间为\(O(n+k)\)。

计算机发展史中的重要事件，年份和人物

计算机发展代别划分

代别	年代	逻辑电子元件
第一代	\(1946-1958\)	电子管
第二代	\(1959-1964\)	晶体管
第三代	\(1965-1970\)	集成电路
第四代	\(1970-\text{now}\)	大规模超大规模集成电路

重要事件

• \(1936\)年英国数学家图灵提出了图灵机的概念，\(1950\)年提出了图灵试验。

• \(1944\)年，美籍匈牙利数学家冯诺依曼提出计算机基本结构和工作方式的设想，其理论要点为：\(1.\) 计算机硬件由存储器，运算器，控制器，输入输出设备组成。\(2.\) 储存程序思想。至今为止计算机人采用冯诺依曼架构。

• \(1946\)年\(2\)月，在美国宾夕法尼亚大学诞生了世界上第一台电子计算机\(\text{ENIAC}\)。

• \(1966\)年图灵奖设立，唯一获奖的华裔计算机科学家姚期智在\(2000\)年获奖。

• \(1971\)年英特尔公司推出了世界上第一款微处理器\(4004\)，字长是\(4\)位，是\(4\)为微处理器。

• \(1978\)年英特尔公司推出的\(8086\)是第一个\(16\)位的微处理器。

• \(1985\)年英特尔公司生产出\(32\)位字长的处理器\(80836\)。

• \(1989\)年我国第一个公用分组交换网\(\text{CNPAC}\)建成运行。

• \(1993\)年英特尔公司生产出\(64\)位字长的处理器\(80586\)，名为\(\text{Pentium}\)。

重要人物

• 美籍匈牙利数学家 \(\text{John von Neumann}\)

冯诺伊曼对世界上第一台电子计算机\(\text{ENIAC}\)（电子数字积分计算机）的设计提出过建议，\(1945\)年\(3\)月他在共同讨论的基础上起草了一个全新的“存储程序通用电子计算机方案”——\(\text{EDVAC}\)（\(\text{Electronic Discrete Variable Automatic Computer}\)的缩写）。这对后来计算机的设计有决定性的影响，特别是确定计算机的结构，采用存储程序以及二进制编码等，至今仍为电子计算机设计者所遵循。

\(1946\)年，冯·诺依曼开始研究程序编制问题，他是现代数值分析——计算数学的缔造者之一，他首先研究线性代数和算术的数值计算，后来着重研究非线性微分方程的离散化以及稳定问题，并给出误差的估计。他协助发展了一些算法，特别是蒙特卡罗方法。

• 英国数学家，逻辑学家 \(\text{Alan Mathison Turing}\)

\(1931\)年图灵进入剑桥大学国王学院，毕业后到美国普林斯顿大学攻读博士学位，第二次世界大战爆发后回到剑桥，后曾协助军方破解德国的著名密码系统\(\text{Enigma}\)，帮助盟军取得了二战的胜利。

图灵对于人工智能的发展有诸多贡献，提出了一种用于判定机器是否具有智能的试验方法，即图灵试验，至今，每年都有试验的比赛。此外，图灵提出的著名的图灵机模型为现代计算机的逻辑工作方式奠定了基础。

图灵奖于\(1966\)年由美国计算机协会\(\text{ACM}\)设立，专门奖励那些对计算机事业做出重要贡献的个人。

• 英国数学家，程序员 \(\text{Ada Lovelace}\)

著名英国诗人拜伦之女，计算机程序创始人，建立了循环和子程序概念。

为计算程序拟定“算法”，写作的第一份“程序设计流程图”，被珍视为“第一位给计算机写程序的人”。为了纪念阿达·奥古斯塔对现代电脑与软件工程所产生的重大影响，美国国防部将耗费巨资，历时近\(20\)年研制成功的高级程序语言命名为\(\text{Ada}\)语言，它被公认为是第四代计算机语言的主要代表。

• 美国计算机科学家 \(\text{John McCarthy}\)

\(1971\)年的图灵奖授予提出“人工智能”这一术语并使之成为一个重要的学科领域的斯坦福大学教授约翰·麦卡锡。

• 英国数学家，机械工程师 \(\text{Charles Babbage}\)

查尔斯·巴比奇由于提出了差分机与分析机的设计概念，被视为计算机先驱。\(1828\)年至\(1839\)年，巴比奇曾在剑桥大学担任卢卡斯数学教授席位。

• 英国数学家，信息论创始人 \(\text{Claude Elwood Shannon}\)

香农于\(1940\)年在普林斯顿高级研究所期间开始思考信息论与有效通信系统的问题。经过\(8\)年的努力，香农在\(1948\)年\(6\)月和\(10\)月在《贝尔系统技术杂志》（\(\text{Bell System Technical Journal}\)）上连载发表了具有深远影响的论文《通讯的数学原理》。\(1949\)年，香农又在该杂志上发表了另一著名论文《噪声下的通信》。在这两篇论文中，香农阐明了通信的基本问题，给出了通信系统的模型，提出了信息量的数学表达式，并解决了信道容量、信源统计特性、信源编码、信道编码等一系列基本技术问题。两篇论文成为了信息论的奠基性著作。

• 美国科学家，英特尔公司创始人 \(\text{Gordon Moore}\)

创立\(\text{Inter}\)公司，提出摩尔定律：集成电路上可以容纳的晶体管数目在大约每经过\(24\)个月便会增加一倍。换言之，处理器的性能每隔两年翻一倍。

• 荷兰计算机科学家 \(\text{Edsger Wybe Dijkstra}\)

曾在\(1972\)年获得图灵奖，之后，他还获得过\(1974\)年\(\text{AFIPS Harry Goode Memorial Award}\)，\(1989\)年\(\text{ACM SIGCSE}\)计算机科学教育教学杰出贡献奖，以及\(2002\)年\(\text{ACM PODC}\)最具影响力论文奖。提出了著名的贪心最短路算法\(\text{Dijkstra}\)。

• 美国计算机科学家 \(\text{Robert Tarjan}\)

罗伯特·塔扬与约翰霍普克罗夫特共同于\(1986\)年获得图灵奖。罗伯特·塔扬证明了并查集时间复杂度，提出图论连通性的\(\text{Trajan}\)算法，离线求解树上最近公共祖先的\(\text{Trajan}\)算法，提出\(\text{Splay}\)树，动态树，斐波那契堆等数据结构。

计算机语言

机器语言

用二进制代码来编写计算机程序，又称二进制语言，书写困难，记忆复杂，难以掌握。

汇编语言

比机器语言简单，但仍属于低级语言，工作量大，繁琐，可移植性差。

graph LR 1[汇编源程序] --翻译程序--> 2[目标程序] 2[目标程序] --连接程序--> 3[可执行程序]

高级语言

通过翻译程序翻译成机器语言形式的目标程序，翻译有两种方式：编译方式和解释方式。

编译方式：由编译程序将源程序转化成二进制代码，生成目标程序，然后把目标程序连接成可执行程序。

graph LR 1[高级语言源程序] --编译程序--> 2[目标程序] 2[目标程序] --连接程序--> 3[可执行程序]

解释方式：源程序进入计算机时，解释程序边扫描边解释，解释一条执行一条，不产生目标程序。

graph LR 1[高级语言源程序] --解释程序--> 2[可执行程序]

常见的计算机语言

编译性语言：\(\text{C/C++, Pascal/Object, Fortran, Cobol, Delphi}\)。

解释性语言：\(\text{ASP, PHP, Java, JavaScript, VBScript, Perl, Python, Ruby, MATLAB}\)。

面向对象语言：\(\text{Simula 67, Smalltalk, EIFFEL, C++, Java, C#, Python, Go}\)。

面向过程语言：\(\text{Fortran, C}\)。

References

\([1]\text{zqy}.(2005).\text{Fake with its applications,6(66),1-114514}.\)

\([2]\text{zqy's blogs : cnblogs},\)云烟万象但过眼\(.\)