博弈论入门——经典模型
博弈 ——\(Alice\) 遇到了\(Bob\)
博弈论题型概述:
- 有两名选手\(Alice\)和\(Bob\)交替进行预先规定好的操作。
- 任意时刻,可以执行的合法操作只取决于情况本身,与选手无关
- 失败取决于选手无法进行合法操作
一.巴什博弈 \(~~Bash~~Game\)
一堆\(n\)个物品,两个人轮流从中取出\(1\)~\(m\)个,不能继续取的人输。
结论:\((m+1)|n\)时先手必败
考虑两种特殊的状态:
状态1:考虑\(n \le m\)的情况,先手可以直接取完,此时先手必胜。
状态2:考虑\(n =m+1\)的情况,先手必然不能取完,此时先手必败。
显然存在 \(n = k*(m+1)+r\)
假如\((m+1)|n\),即\(r = 0\),先手取走\(x\)个,后手可以取\((m+1)-x\)个,即无论先手取多少个,后手一定可以保证石子个数整除\(m+1\)。所以最后一定可以回归到状态二
此时先手必败
反之,\(r\neq0\),先手拿\(r\)个石子,后手陷入上述的必败局面。
例题:
二.尼姆博弈 \(~~Nim ~~Game\)
有\(n\)堆石子,两个人可以从任意一堆石子中拿任意多个石子(不能不拿),取光者胜利
结论:当\(n\)堆石子的数量异或和等于\(0\)时,先手必败
定义:\(x\oplus y\)表示\(x\)异或\(y\),\(Nim\)和为所有石子的异或和。
(个人觉得这个证明蛮重要的)
证明:
先认可三件事:
第一:存在至少一种最简单的必败状态,这种状态无法进行任何操作。
第二:先手必胜就是一定存在先手进行了一步操作之后,后手再进行操作必败
即必胜态一定存在一种移动变成必败态
第三:先手必败就是不存在先手进行了一步操作之后,后手进行操作必败
即必败态不存在一种移动变成必败态
一种显然的状态:当所有的石子数为\(0\)时,显然此时必败。
有\(a_1\oplus a_2\oplus ...\oplus a_n = 0\)。
定理1:我们称这样没有后继状态的状态为必败基态(自己取得名字)
考虑其他状态之前我们先来想清楚一个问题,\(x\)个\(0\)和\(y\)个\(1\)的异或和是多少?
\(0\)异或任何数字都是\(0\),而\(1\oplus 1 = 0\),推广一下就是偶数个\(1\)异或和为\(0\)。
所以当且仅当\(y\)为奇数的时候,\(x\)个\(0\)和\(y\)个\(1\)的异或和为\(1\),反之为\(0\)。
也就是异或和为1时,\(y\)至少为1。(这句才是重点)
现在考虑其他状态:
令 \(k = a_1\oplus a_2...\oplus a_i \oplus... \oplus a_n\)。
假如\(k\neq0\):(我们认为的先手必胜状态)
设\(k\)的二进制最高位为\(x\),此位置一定为1,从上文可知,至少存在一个\(a_i\)的二进制在\(x\)上为\(1\),找到其中一个\(a_i\),使得\(a_{i}' = a_i\oplus k\),只考虑第\(x\)位,这一位的\(1\)变成了\(0\),这势必使得\(a_{i}' < a_i\),所以我们一定可以在\(a_i\)中拿走若干石子,使其石子数变成\(a_i'\)。
此时,\(Nim\)和变成了
\(k\oplus k= a_1\oplus a_2...\oplus a_i \oplus k\oplus... \oplus a_n = 0\)。
也就是说:\(k\neq0\)的状态一定可以转换成\(k=0\)的状态
更常见的陈述是下面这个:
定理2:任意\(a_1\oplus a_2...\oplus a_i \oplus... \oplus a_n \neq 0\)的局面,一定存在一种移动得到\(a_1\oplus a_2...\oplus a_i \oplus... \oplus a_n = 0\)
(必胜态一定存在一种移动变成必败态)
假设\(k = 0\):
参考上面的过程,我们只需要证明必败态不存在一种移动变成必败态,也就是现在的\(k=0\)无法经过一步操作变成另一个\(k=0\)(这一段解释的不是很好)。
考虑反证法:
假设存在移动过后存在:
\(a_1\oplus a_2...\oplus a_i' \oplus... \oplus a_n = 0\)
上面我们已经知道移动过后\(a_i' < a_i\)。
又知道,
\(a_1\oplus a_2...\oplus a_i \oplus... \oplus a_n = 0\)。
两式存在大量相同的数字,不妨将两式异或。
得到\(a_i\oplus a_i' = 0\),即\(a_i = a_i'\)。
矛盾。
得证定理3:
任意\(a_1\oplus a_2...\oplus a_i \oplus... \oplus a_n = 0\)的局面,一定不存在一种移动得到\(a_1\oplus a_2...\oplus a_i \oplus... \oplus a_n = 0\)
(必败态一定不存在一种移动变成必败态)
证明结束
例题
三.威佐夫博弈 \(~~Wythoff ~~Game\)
有两堆各若干物品,分别为\(n\),\(m\),\((n\le m)\)两个人轮流从任意一堆中至少取出一个或者从两堆中取出同样多的物品,规定每次至少取一个,至多不限,最后取光者胜。
结论:先手必败,当且仅当,\((m-n)\frac{(\sqrt5+1)}{2} = n\),注意黄金分割比需要向下取整
证明
手玩一下我们发现有一些情况是先手必败的。比如(0,0),(1,2),(3,5)等等。
以(1,2)为例分析一下:
先手取走第一堆,后手取完第二堆,后手胜。
先手在第二堆中取走1个,后手两堆都取一个,后手胜。
先手取完第二堆,后手取第一堆,后手胜。
先手取两堆都取一个,后手取完第二堆,后手胜利。
继续手玩几个状态,\((0,0),(1,2),(3,5),(4,7)\)...【认定前面的小于后面的】
发现一个神奇的规律:第\(k\)个必败状态是\((x,y)\)【\(k\)从\(0\)开始】,并且\(y = x+k\)。
也就说必败状态两个数的差值是严格递增的。
证明这个规律很简单:假设\((a,a+k),(b,b+k),b > a\)两个必败状态,显然可以使\(b\)状态转移到\(a\)状态,但是在前面\(Nim\)游戏的证明中我们已经得知,必败状态不会转移到必败状态,所以矛盾。
不妨做一张坐标图来观察,把两堆石子的数量看作是坐标轴上的点。
现在这个博弈又当如何?
每个人都可以把这个点向左、向下或者向左下移动若干步,移动到原点\((0,0)\)处的人胜利。
标记刚才的必败点:
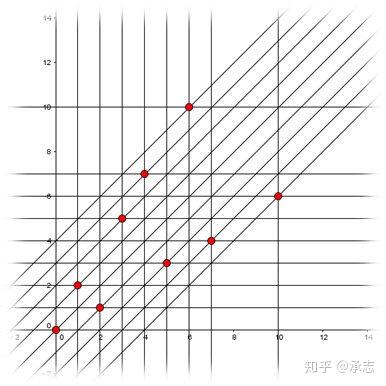
显然,除了必败点都是必胜点。
现在的问题是,对于给定的\((x,y)\)如何判断它是不是某一个必败局面\((x_k,y_k)\)
抛出一个定理——\(Betty\)定理:
设a和b是两个正无理数,并且
\(\frac{1}{a}+\frac{1}{b} = 1\) ,
记\(P=\{[na],n\in N^{+} \}, Q=\{[nb],\in N^{+} \}\),则\(P\cap Q = \empty\),\(P\cup Q=N^{+}\)
假设存在一对\(a,b\)即符合\(Betty\)定理又符合必败状态的通项\((x_n = an,y_n=bn)\)。

解方程可得:
\(a = \frac{1+\sqrt {5}}{2} = 1.618\),恰好符合黄金分割比。
例题
四.斐波那契博弈 \(~~Fibonacci~~Game\)
一堆石子有\(n\)个,两人轮流取,先取者第一次可以去任意多个,但是不能取完,以后每次取的石子数不能超过上次取子数的\(2\)倍。取完者胜。
结论:先手必败,当且仅当石子数为斐波那契数
证明参考
证明:
证明n为\(Fibonacci\)数列时,先手必败:
令\(n\)为\(Fibonacci\)数列的第\(i\)项,\(f[i] = n\)。
用第二类数学归纳法证明:
1、当\(i = 2\)时,先手只能取\(1\)颗,此时必败
2、假设当\(i <= k\)时,结论成立(下文称之为假设2)
3、当 \(i = k+1\),有\(f[i] = f[k]+f[k-1]\)。
则我们可以把这一堆石子转换为两堆石子,分别为\(f[k]\)与\(f[k-1]\)。
如果先手取的石子数大于\(f[k-1]\),则后手一定可以取完,因为\(f[k] = f[k-1]+f[k-2]< 2*f[k-1]\),此时先手必败。
也就是说,先手只能在\(f[k-1]\)这一堆取石子。
由之前的假设2可知,后手必胜,也就是最后一次在\(f[k-1]\)取石子的是后手。
令最后一手拿了\(x\)枚石子,此时可知如果\(2*x\geq f[k]\),先手就可以把\(f[k]\)全部拿走,此时先手必胜,因为如果不能全部拿走有假设2可知此时先手必败。
考虑\(x\)最大的情况,即先手拿了\(\frac{f[k-1]}{3}\),后手直接将剩下的\(\frac{2*f[k-1]}{3}\)全部拿走。(这个很好理解的吧。。。)
现在比较\(\frac{4*f[k-1]}{3}\)和\(f[k]\)的大小关系。
做差可得(斐波那契递推):
\(~~~~3*f[k]-4*f[k-1]
\\= 3*f[k-2]-f[k-1]
\\=2*f[k-2]+f[k-3] >0\)
即\(3*f[k]<4*f[k-1]\),可得\(\frac{4*f[k-1]}{3}<f[k]\)
也就是说先手无法一次性全部取完\(f[k]\),所以先后必败
即\(i=k+1\)时,结论依然成立。
证明\(n\)不是\(Fibonacci\)数列时,先手必胜:
先声明一个定理:
齐肯多夫定理:任何正整数可以表示为若干个不连续的\(Fibonacci\)数。
根据这个定理我们可以将石子数\(n\)表达为若干个不连续\(Fibonacci\)数。
表达时,尽可能取最大的\(Fibonacci\)数。
\(n = f[a_1]+f[a_2]+...+f[a_p]\)(降序排列)
先手取最小的\(f[a_p]\),由于不连续,易得\(f[a_{p-1}] > 2*f[a_p]\)。故,后手仅仅只能在\(f[a_{p-1}]\)这一堆取,并且取不完。这个问题就是之前证明的石子数为\(Fibonacci\)数必败的情况。
一次类推,每一堆均必败,此时先手必胜。
模板
证明完毕。
五.相关定理证明
齐肯多夫定理 的证明:
证明参考
\(f[]\)表示\(Fibonacci\)数列
考虑数学归纳法
对于任意的正整数\(n\):
假设\(i < n\)时成立。
1.如果\(n\)为\(Fibonacci\)数,成立
2.如果\(n\)不为\(Fibonacci\)数,
设\(k_1\)使得\(f[k_1] < n < f[k_1+1]\),\(d = n- f[k_1]\)
得\(d = n-f[k_1] < f[k_1+1]-f[k_1] = f[k_1-1]\)
归纳假设,\(d<n\)所以\(d\)也可以表达为若干个不连续 \(Fibonacci\)数的和。
设为\(d = f[k_2] + f[k_3]...(k_2 > k_3 ...)\)
只需证明,\(k_2\)与\(k_1\)不连续即可。
\(f[k_2] < d < f[k_1-1]<f[k_1]\)。故\(k_2\)与\(k_1\)不连续。
证毕。
\(Betty\)定理的证明
参考这一篇
(没看懂,暂时鸽了)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号