软件工程第三次作业
个人信息
| 姓名 | 学号 |
|---|---|
| 王文俊 | 3121004966 |
(因为周围找不到使用C++的同学,所以就一个人做了
作业概述
| 这个作业属于哪个课程 | 软件工程 |
|---|---|
| 这个作业要求在哪里 | 结对项目 |
| 这个作业的目标 | 实现四则运算题目的命令行程序 |
一、GitHub链接
https://github.com/Paradox-17/4_Arithmetic_Generator
二、PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 1380 | 2045 |
| · Analysis | · 需求分析 (包括学习新技术) | 180 | 102 |
| · Design Spec | · 生成设计文档 | 30 | 28 |
| · Design Review | · 设计复审 | 10 | 7 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 3 |
| · Design | · 具体设计 | 20 | 15 |
| · Coding | · 具体编码 | 1000 | 1780 |
| · Code Review | · 代码复审 | 10 | 13 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 97 |
| Reporting | 报告 | 45 | 37 |
| · Test Report | · 测试报告 | 25 | 17 |
| · Size Measurement | · 计算工作量 | 10 | 7 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 10 | 13 |
| · 合计 | 1435 | 2092 |
三、需求分析
题目
实现一个自动生成小学四则运算题目的命令行程序
具体要求
- 使用 -n 参数控制生成题目的个数
- 使用 -r 参数控制题目中数值(自然数、真分数和真分数分母)的范围,该参数必须给定,否则程序报错并给出帮助信息
- 生成的题目中计算过程不能产生负数,也就是说算术表达式中如果存在形如e1− e2的子表达式,那么e1≥ e2
- 生成的题目中如果存在形如e1÷ e2的子表达式,那么其结果应是真分数
- 每道题目中出现的运算符个数不超过3个
- 程序一次运行生成的题目不能重复,即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目,生成的题目存入执行程序的当前目录下的Exercises.txt文件
- 在生成题目的同时,计算出所有题目的答案,并存入执行程序的当前目录下的Answers.txt文件
- 程序应能支持一万道题目的生成
- 程序支持对给定的题目文件和答案文件,判定答案中的对错并进行数量统计,统计结果输出到文件Grade.txt
四、具体实现
模块设计

- SqStack:顺序栈相关操作
- Basic_Arithmetic_Operation:基本算数运算
- Check:校验判断
- Generator:算式及答案生成的相关操作
数据结构设计
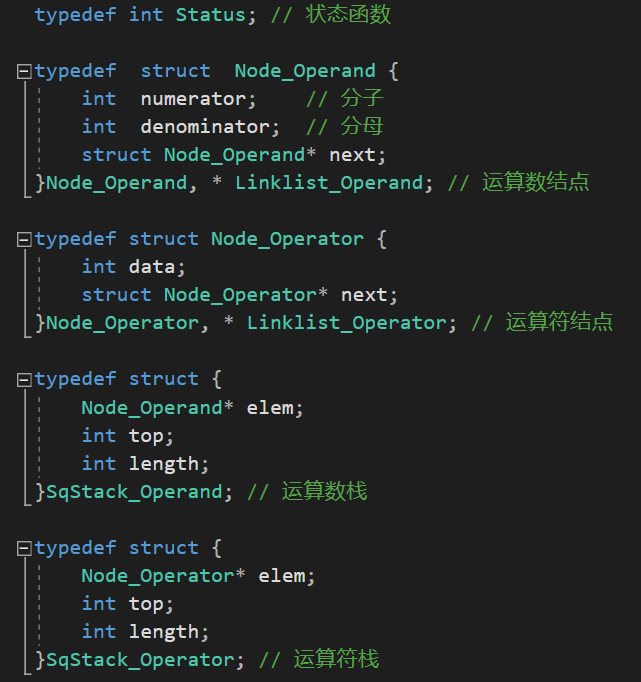
函数列表
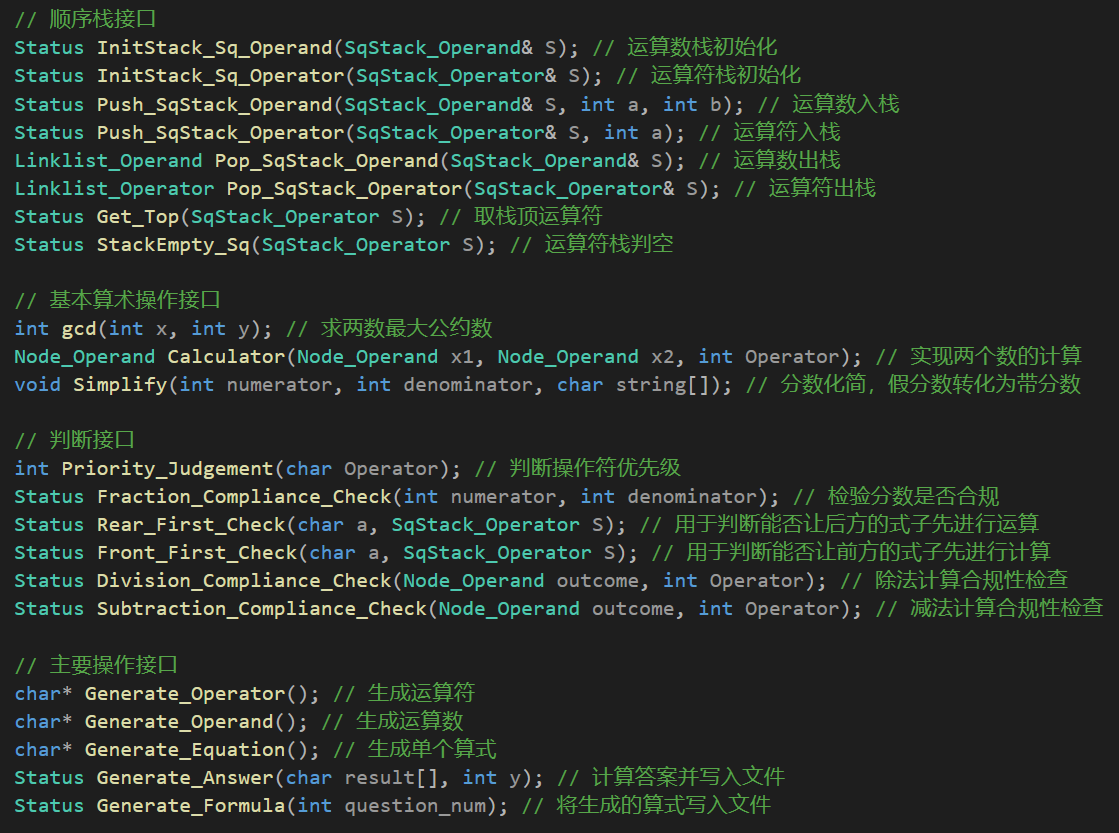
函数调用关系

核心代码
1、生成单个算式
char* Generate_Equation() // 生成单个算式
{
srand((unsigned)time(NULL) + rand());
int parenthesis = 0; // parenthesis用于标志算式是否存在未配对的左括号,1表示存在
int quantity_operand = rand() % 3 + 2; // 操作数个数,取值范围2、3、4
char string[MAXSIZE] = {}; // 用于存放算式
// 算式超过两个操作数,算式最前方有几率出现括号
if (quantity_operand > 2)
{
if (rand() % 2 == 1) // 生成概率为1/2
{
strcat(string, "(");
parenthesis = 1;
}
}
// 依次生成数字、算符、数字
strcat(string, Generate_Operand());
strcat(string, Generate_Operator());
strcat(string, Generate_Operand());
if (quantity_operand == 2) return string; // 若此次生成的算式仅有两个操作数,则生成完毕
// 此次生成的算式操作数个数大于2,继续生成
else
{
if (parenthesis == 1) // 若存在未配对的左括号
{
if (rand() % 2 == 1) // 1/2的概率生成对应右括号
{
strcat(string, ")");
parenthesis = 0;
}
}
// 生成一个算符
strcat(string, Generate_Operator());
// 若此次生成的为4个操作数的算式,且此时算式中无未配对的左括号,则仍可以插入左括号,概率为1/2
if (quantity_operand == 4 && parenthesis == 0)
{
if (rand() % 2 == 1)
{
strcat(string, "(");
parenthesis = 1;
}
}
// 生成一个数字
strcat(string, Generate_Operand());
// 若此次生成的为3个操作数的算式,检查是否存在未配对左括号,并结束此次生成
if (quantity_operand == 3)
{
if (parenthesis == 1)
{
strcat(string, ")");
parenthesis = 0;
}
return string;
}
// 若此次生成的为4个操作数的算式,生成最后的算符与数字,随后检查是否存在未配对左括号,并结束此次生成
if (quantity_operand == 4)
{
strcat(string, Generate_Operator());
strcat(string, Generate_Operand());
if (parenthesis == 1)
{
strcat(string, ")");
parenthesis = 0;
}
return string;
}
}
}
2、生成答案
Status Generate_Answer(char result[], int y) // 计算答案并写入文件
{
extern int count; // 用于记录算式个数
SqStack_Operand S_operand; // 运算数栈
SqStack_Operator S_operator; // 运算符栈
Linklist_Operand operand_x1, operand_x2; // 操作数
Node_Operand outcome; // 存放结果或中间结果
int i = 0, j = 0;
int Operator;
char answer[20] = {}; // 用于存放答案
FILE* fp;
InitStack_Sq_Operand(S_operand);
InitStack_Sq_Operator(S_operator);
fp = fopen("Answer.txt", "a");
while (result[i] != '\0' || StackEmpty_Sq(S_operator) != OK) // 按字符依次读取
{
if (result[i] >= '0' && result[i] <= '9') // 若读取到数字
{
j = j * 10 + (result[i] - '0'); // 还原数字
i++;
if (result[i] > '9' || result[i] < '0') // 若下一个字符为算符,则将读取到的数字压入操作数栈
{
Push_SqStack_Operand(S_operand, j, 1);
j = 0;
}
}
else // 若读取到运算符
{
if (result[i] == ')' && Get_Top(S_operator) == '(') // 若出现一个操作数前后均有括号的情况,则去除冗余的括号
{
Pop_SqStack_Operator(S_operator); // 移除左括号
i++;
continue;
}
if (Rear_First_Check(result[i], S_operator) == OK) // 满足能够让后方的式子先进行运算的条件
{
Push_SqStack_Operator(S_operator, result[i]); // 运算符入栈
i++;
continue;
}
if (Front_First_Check(result[i], S_operator) == OK) // 之前已读入的算式能够先进行计算
{
operand_x1 = Pop_SqStack_Operand(S_operand);
operand_x2 = Pop_SqStack_Operand(S_operand);
Operator = Pop_SqStack_Operator(S_operator)->data;
outcome = Calculator(*operand_x1, *operand_x2, Operator); // 计算中间值
// 若除法运算中结果出现假分数,或减法运算中出现负数,则向上层函数报错
if (Division_Compliance_Check(outcome, Operator) == ERROR || Subtraction_Compliance_Check(outcome, Operator) == ERROR)
{
fclose(fp);
return ERROR;
}
Push_SqStack_Operand(S_operand, outcome.numerator, outcome.denominator); // 算式符合规范,中间结果入栈
continue;
}
}
}
if (outcome.numerator < 0) // 结果出现负数,返回-1
{
fclose(fp);
return ERROR;
}
Simplify(outcome.numerator, outcome.denominator, answer); // 分式化简,并将结果传入答案字符串
count++;
fprintf(fp, "%d. %s\n", y, answer); // 将答案写入文件
fclose(fp);
return OK;
}
五、性能测试
总览
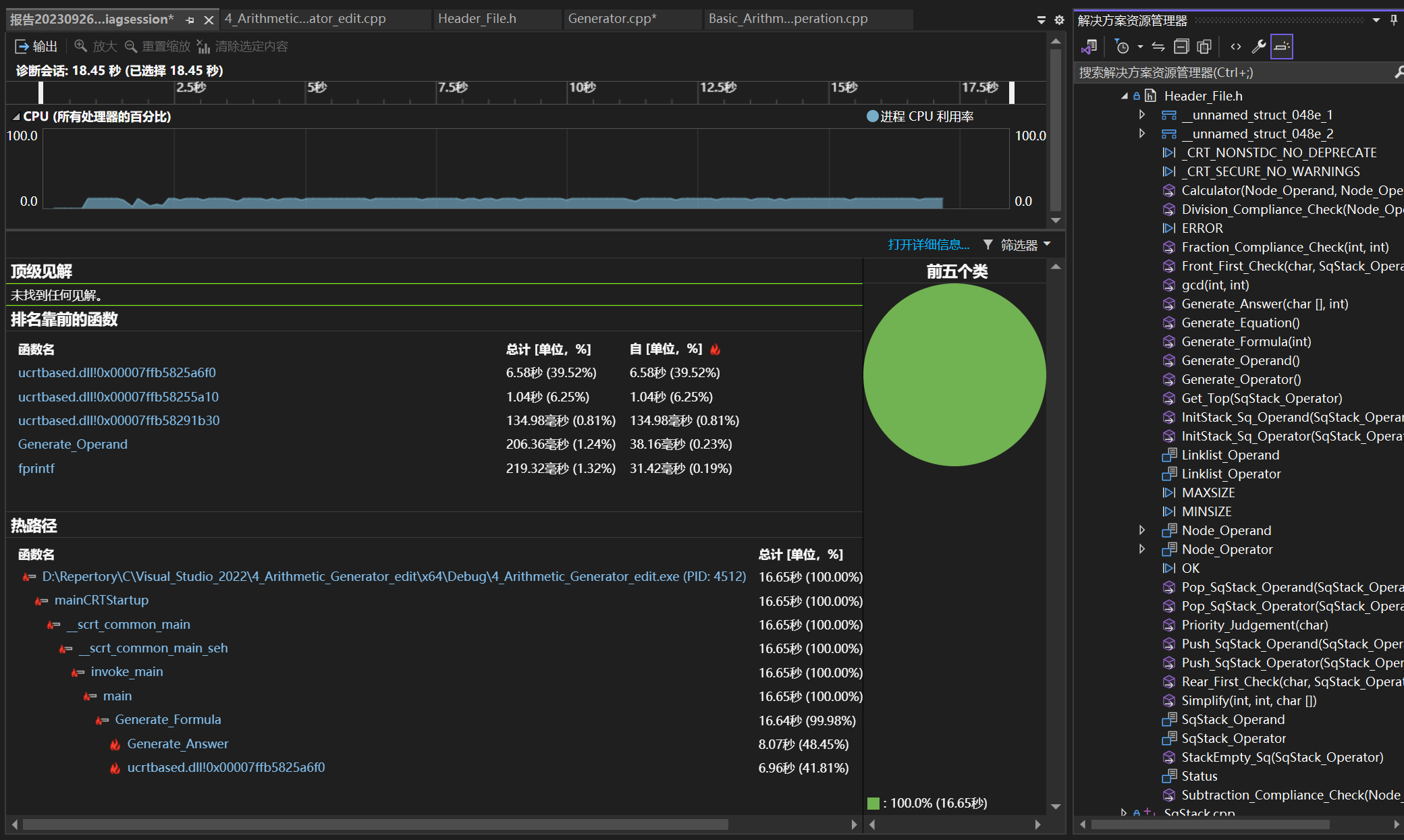
热路径
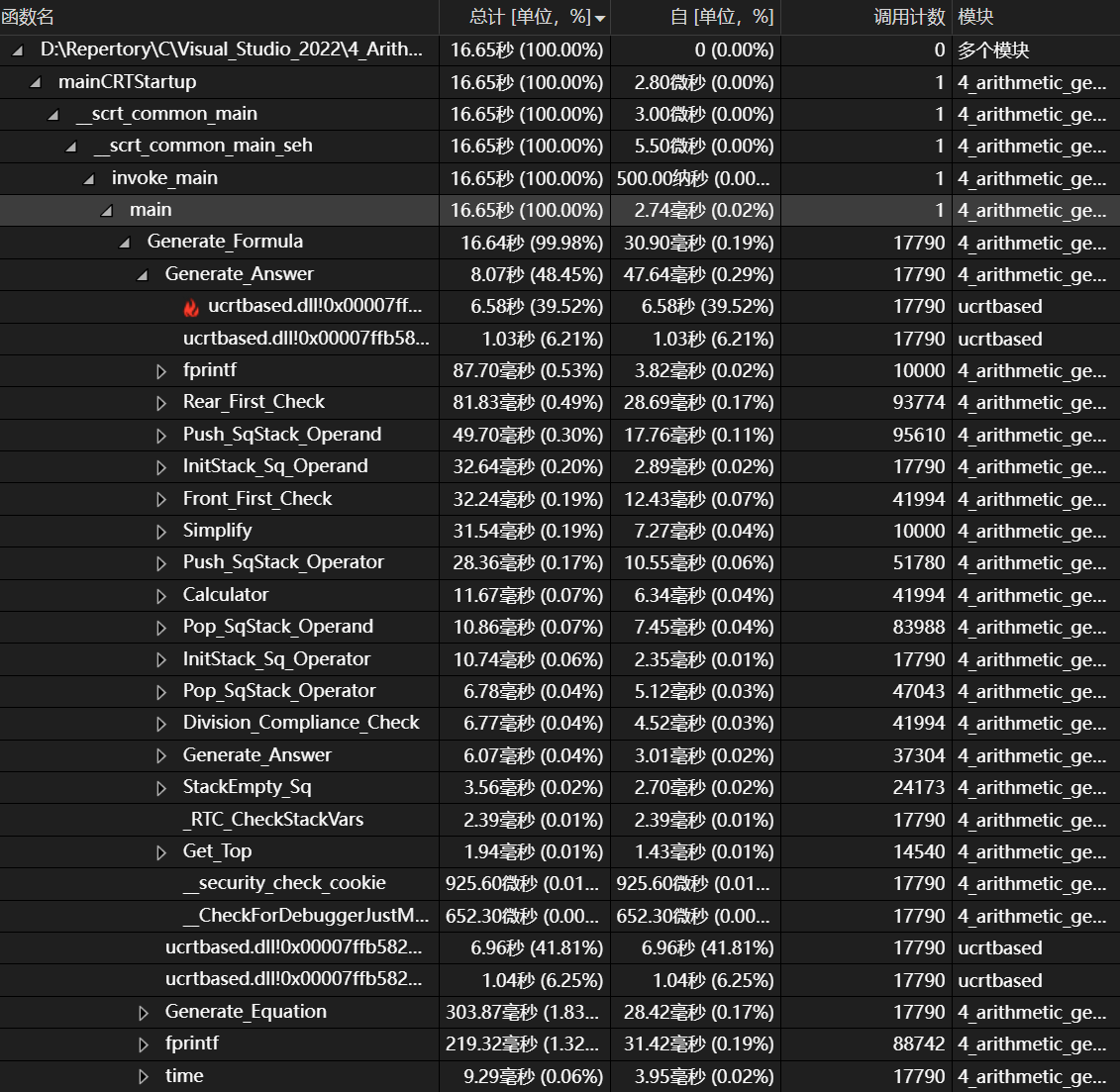
火焰图
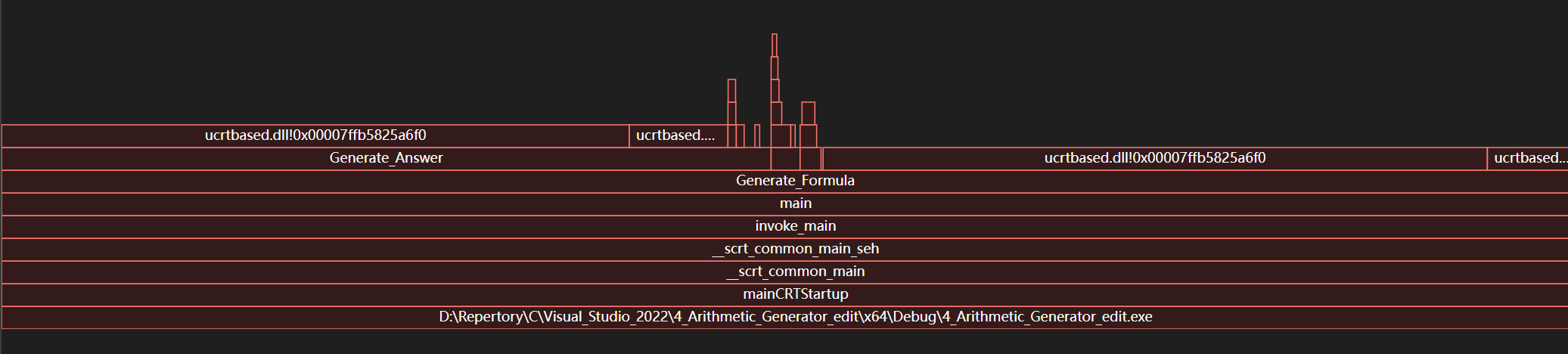
主要函数耗时
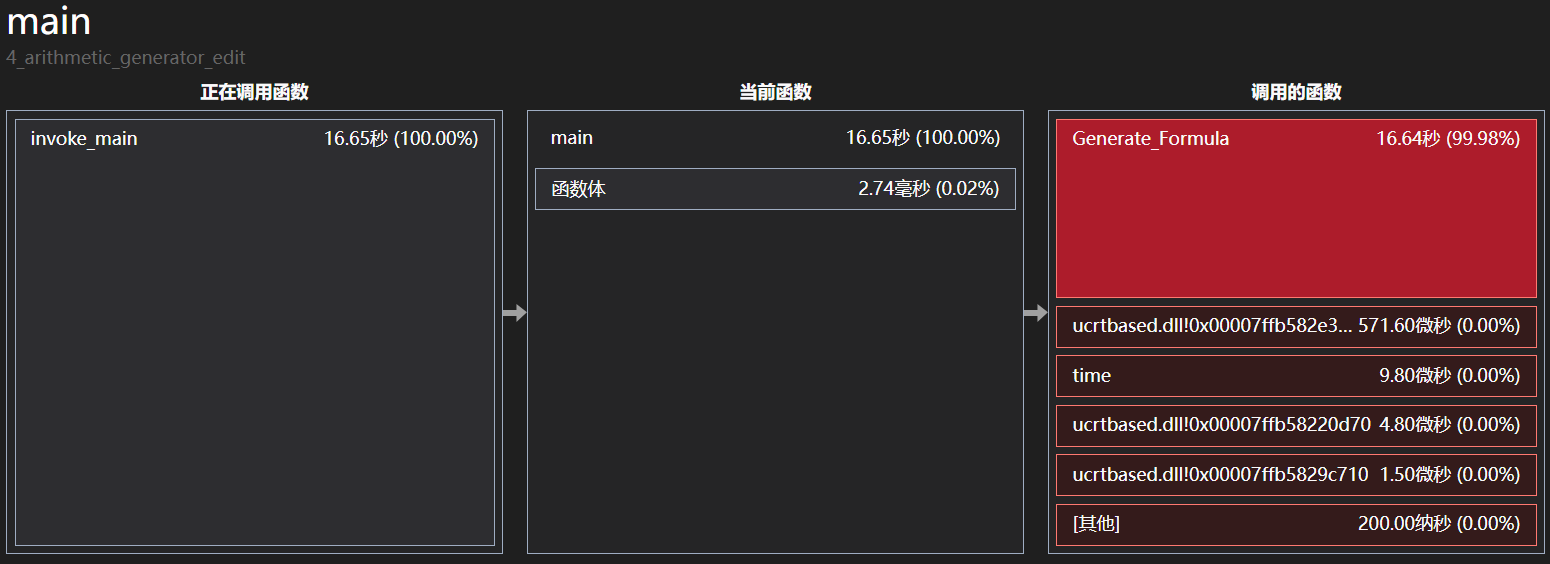
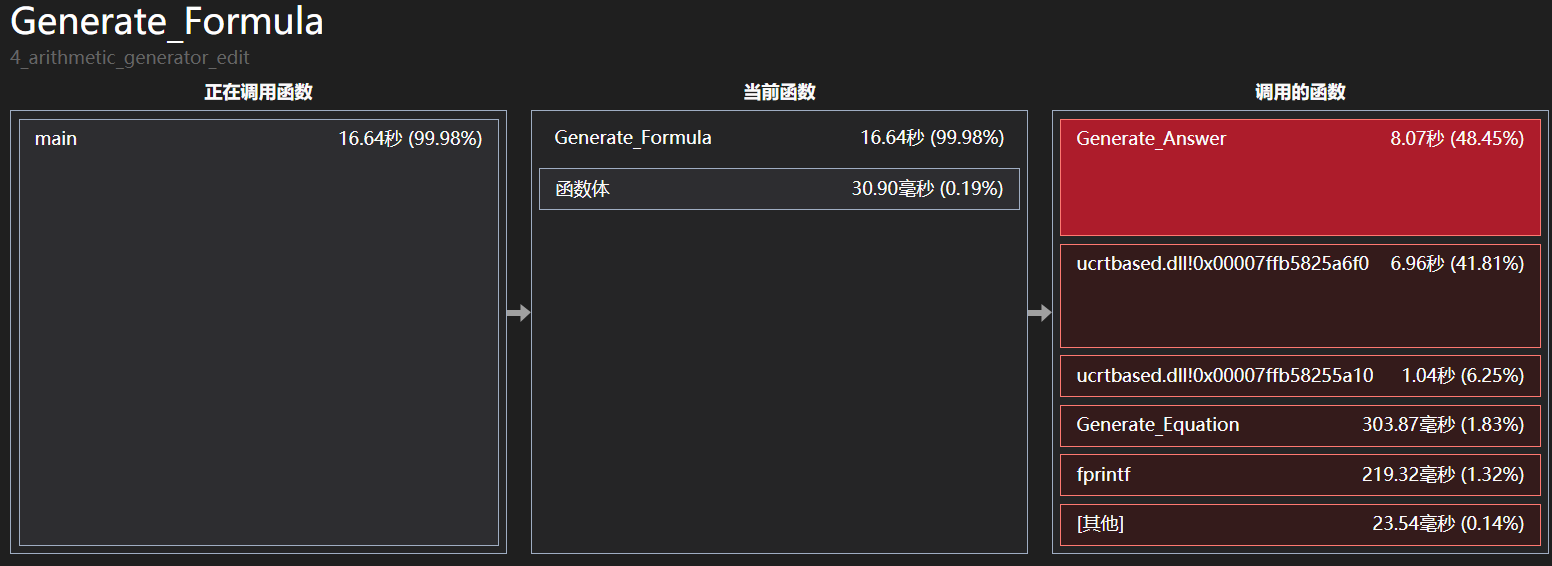
可以看出Generate_Formula函数中Generate_Answer函数被频繁调用
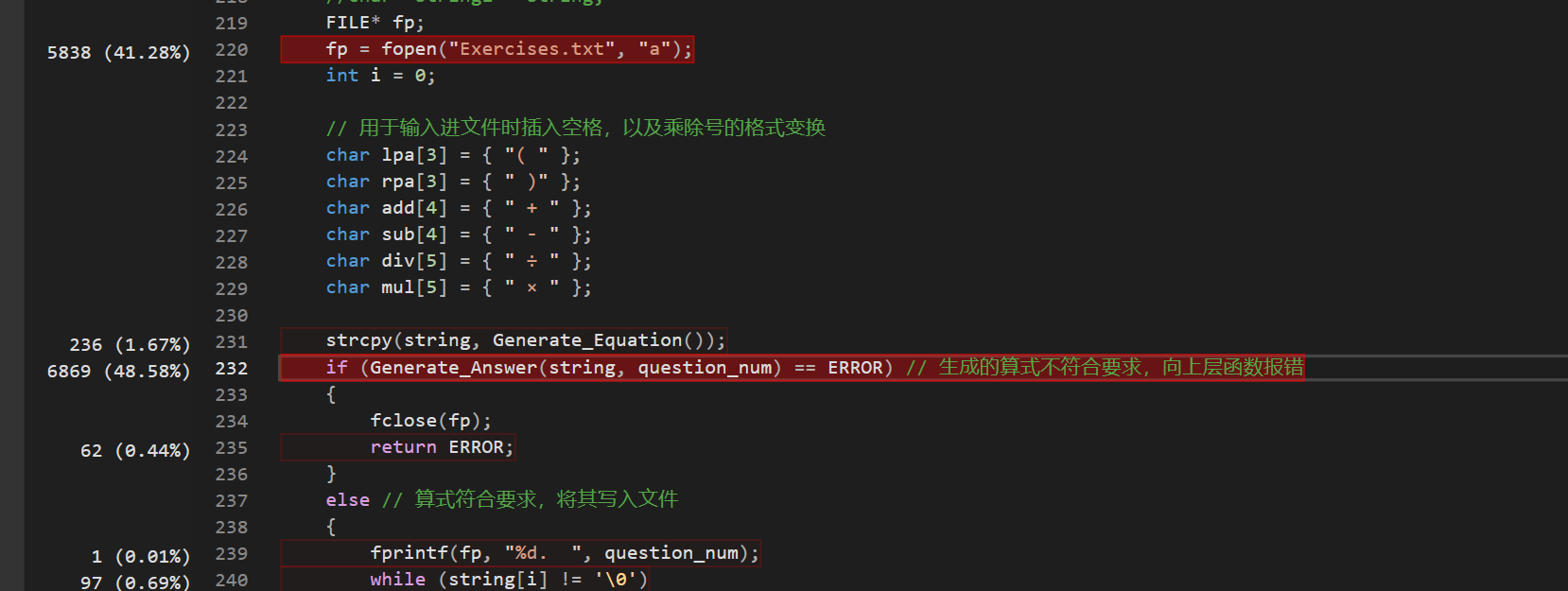
而Generate_Formula函数之所以被频繁调用,是因为生成的算式中,仍有一部分不符合题目要求,导致需要重新生成,故算式生成逻辑仍有优化空间
六、单元测试
-n 10 -r 10


-n 10000 -r 10

七、异常处理
命令行参数输入错误

八、项目小结
项目局限性
1、整体框架还不够清晰
2、生成的算式中,部分不符合题目要求,导致需要重新生成大量算式
改进方法
1、将功能相似的函数进行合并,将一个函数内功能差异较大的部分拆分成多个函数
2、改进优化生成算式的代码逻辑
个人收获
1、对软件开发流程有了基本的了解。拿到一个新项目之后,能够先进行需求分析,设计顶层架构,设计各模块功能,进而设计数据结构,厘清各函数之间的调用关系,最后进行代码的编写。
2、代码编写速度有了一定的提升。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号