第一次个人编程作业
个人信息
| 姓名 | 学号 |
|---|---|
| 王文俊 | 3121004966 |
(因为周围找不到用C++的同学,所以就一个人做了
作业概述
| 这个作业属于哪个课程 | 软件工程 |
|---|---|
| 这个作业要求在哪里 | 结对项目 |
| 这个作业的目标 | 实现生成四则运算题目及答案的命令行程序 |
一、GitHub链接
https://github.com/Paradox-17/3121004966
二、PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 1530 | 2065 |
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 67 |
| · Design Spec | · 生成设计文档 | 30 | 48 |
| · Design Review | · 设计复审 | 20 | 13 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 7 |
| · Design | · 具体设计 | 30 | 75 |
| · Coding | · 具体编码 | 1200 | 1750 |
| · Code Review | · 代码复审 | 20 | 16 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 89 |
| Reporting | 报告 | 60 | 51 |
| · Test Report | · 测试报告 | 30 | 39 |
| · Size Measurement | · 计算工作量 | 10 | 5 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 7 |
| · 合计 | 1600 | 2126 |
三、需求分析
作业题目
实现一个自动生成小学四则运算题目的命令行程序
具体要求
- 使用 -n 参数控制生成题目的个数
- 使用 -r 参数控制题目中数值(自然数、真分数和真分数分母)的范围,该参数必须给定,否则程序报错并给出帮助信息
- 生成的题目中计算过程不能产生负数,也就是说算术表达式中如果存在形如e1− e2的子表达式,那么e1≥ e2
- 生成的题目中如果存在形如e1÷ e2的子表达式,那么其结果应是真分数
- 每道题目中出现的运算符个数不超过3个
- 程序一次运行生成的题目不能重复,即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目,生成的题目存入执行程序的当前目录下的Exercises.txt文件
- 在生成题目的同时,计算出所有题目的答案,并存入执行程序的当前目录下的Answers.txt文件
- 程序应能支持一万道题目的生成
- 程序支持对给定的题目文件和答案文件,判定答案中的对错并进行数量统计,统计结果输出到文件Grade.txt
四、具体实现
模块设计

- SqStack:顺序栈相关操作
- Check:进行检验与判断
- Basic_Arithmetic_Operation:基本算数操作
- Generator:用于生成算式及答案,并写入文件
数据结构设计
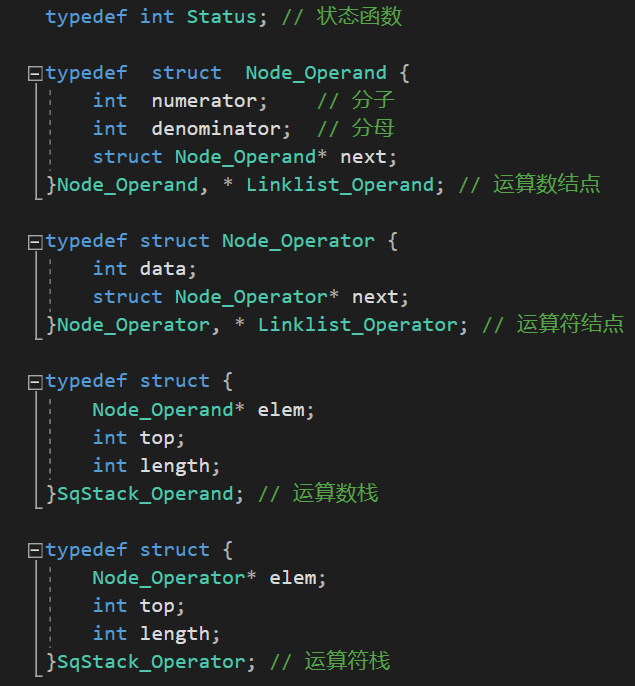
函数列表
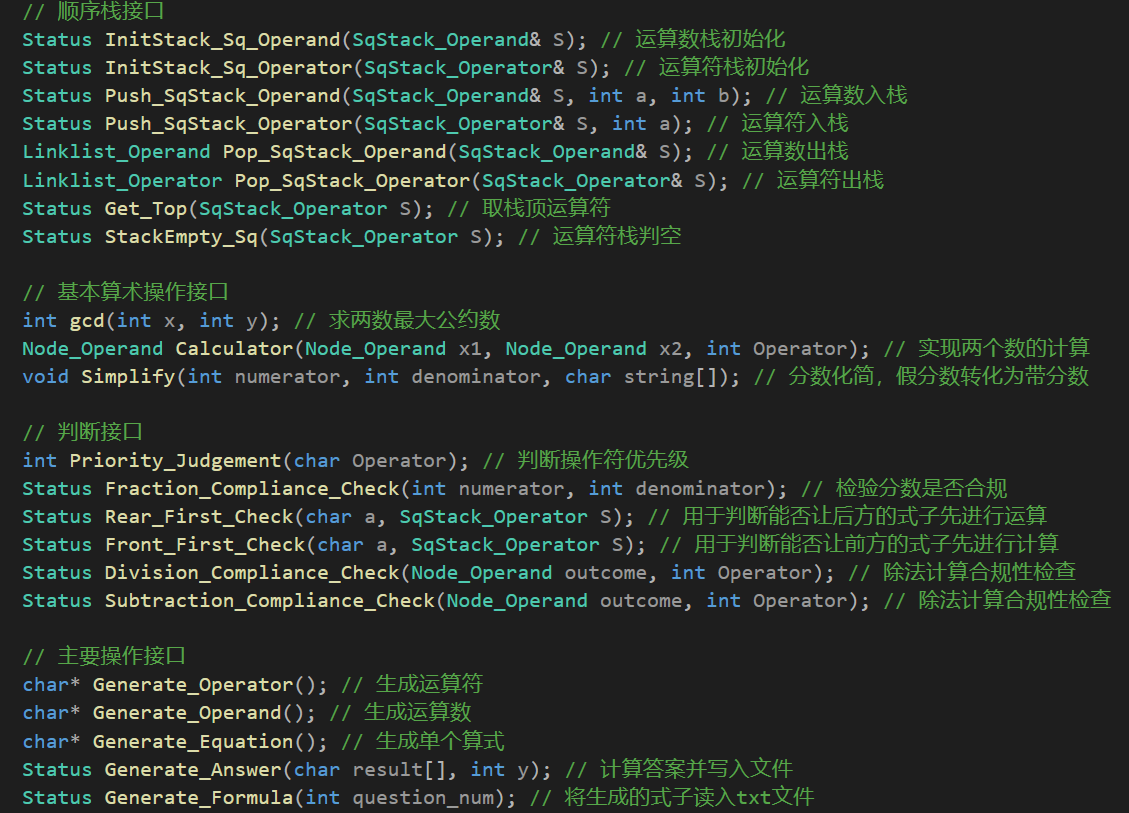
主要函数调用关系

核心代码
生成单个算式
char* Generate_Equation() // 生成单个算式
{
srand((unsigned)time(NULL) + rand());
int parenthesis = 0; // parenthesis用于标志算式是否存在未配对的左括号,1表示存在
int quantity_operand = rand() % 3 + 2; // 操作数个数,取值范围2、3、4
char string[MAXSIZE] = {}; // 用于存放算式
// 算式超过两个操作数,算式最前方有几率出现括号
if (quantity_operand > 2)
if (rand() % 2 == 1) // 生成概率为1/2
{
strcat(string, "(");
parenthesis = 1;
}
// 依次生成数字、算符、数字
strcat(string, Generate_Operand());
strcat(string, Generate_Operator());
strcat(string, Generate_Operand());
if (quantity_operand == 2) return string; // 若此次生成的算式仅有两个操作数,则生成完毕
// 此次生成的算式操作数个数大于2,继续生成
else
{
if (parenthesis == 1) // 若存在未配对的左括号
if (rand() % 2 == 1) // 1/2的概率生成对应右括号
{
strcat(string, ")");
parenthesis = 0;
}
// 生成一个算符
strcat(string, Generate_Operator());
// 若此次生成的为4个操作数的算式,且此时算式中无未配对的左括号,则仍可以插入左括号,概率为1/2
if (quantity_operand == 4 && parenthesis == 0)
if (rand() % 2 == 1)
{
strcat(string, "(");
parenthesis = 1;
}
// 生成一个数字
strcat(string, Generate_Operand());
// 若此次生成的为3个操作数的算式,检查是否存在未配对左括号,并结束此次生成
if (quantity_operand == 3)
{
if (parenthesis == 1)
{
strcat(string, ")");
parenthesis = 0;
}
return string;
}
// 若此次生成的为4个操作数的算式,生成最后的算符与数字,随后检查是否存在未配对左括号,并结束此次生成
if (quantity_operand == 4)
{
strcat(string, Generate_Operator());
strcat(string, Generate_Operand());
if (parenthesis == 1)
{
strcat(string, ")");
parenthesis = 0;
}
return string;
}
}
}
生成答案
Status Generate_Answer(char result[], int y) // 计算答案并写入文件
{
extern int count; // 用于记录算式个数
SqStack_Operand S_operand; // 运算数栈
SqStack_Operator S_operator; // 运算符栈
Linklist_Operand operand_x1, operand_x2; // 操作数
Node_Operand outcome; // 存放结果或中间结果
int i = 0, j = 0;
int Operator;
char answer[20] = {}; // 用于存放答案
FILE* fp;
InitStack_Sq_Operand(S_operand);
InitStack_Sq_Operator(S_operator);
fp = fopen("Answer.txt", "a");
while (result[i] != '\0' || StackEmpty_Sq(S_operator) != OK) // 按字符依次读取
{
if (result[i] >= '0' && result[i] <= '9') // 若读取到数字
{
j = j * 10 + (result[i] - '0'); // 还原数字
i++;
if (result[i] > '9' || result[i] < '0') // 若下一个字符为算符,则将读取到的数字压入操作数栈
{
Push_SqStack_Operand(S_operand, j, 1);
j = 0;
}
}
else // 若读取到运算符
{
if (result[i] == ')' && Get_Top(S_operator) == '(') // 若出现一个操作数前后均有括号的情况,则去除冗余的括号
{
Pop_SqStack_Operator(S_operator); // 移除左括号
i++;
continue;
}
if (Rear_First_Check(result[i], S_operator) == OK) // 满足能够让后方的式子先进行运算的条件
{
Push_SqStack_Operator(S_operator, result[i]); // 运算符入栈
i++;
continue;
}
if (Front_First_Check(result[i], S_operator) == OK) // 之前已读入的算式能够先进行计算
{
operand_x1 = Pop_SqStack_Operand(S_operand);
operand_x2 = Pop_SqStack_Operand(S_operand);
Operator = Pop_SqStack_Operator(S_operator)->data;
outcome = Calculator(*operand_x1, *operand_x2, Operator); // 计算中间值
// 若除法运算中结果出现假分数,或减法运算中出现负数,则向上层函数报错
if (Division_Compliance_Check(outcome, Operator) == ERROR || Subtraction_Compliance_Check(outcome, Operator) == ERROR)
{
fclose(fp);
return ERROR;
}
Push_SqStack_Operand(S_operand, outcome.numerator, outcome.denominator); // 算式符合规范,中间结果入栈
continue;
}
}
}
if (outcome.numerator < 0) // 结果出现负数,返回-1
{
fclose(fp);
return ERROR;
}
Simplify(outcome.numerator, outcome.denominator, answer); // 分式化简,并将结果传入答案字符串
count++;
fprintf(fp, "%d. %s\n", y, answer); // 将答案写入文件
fclose(fp);
return OK;
}
五、性能测试
总览
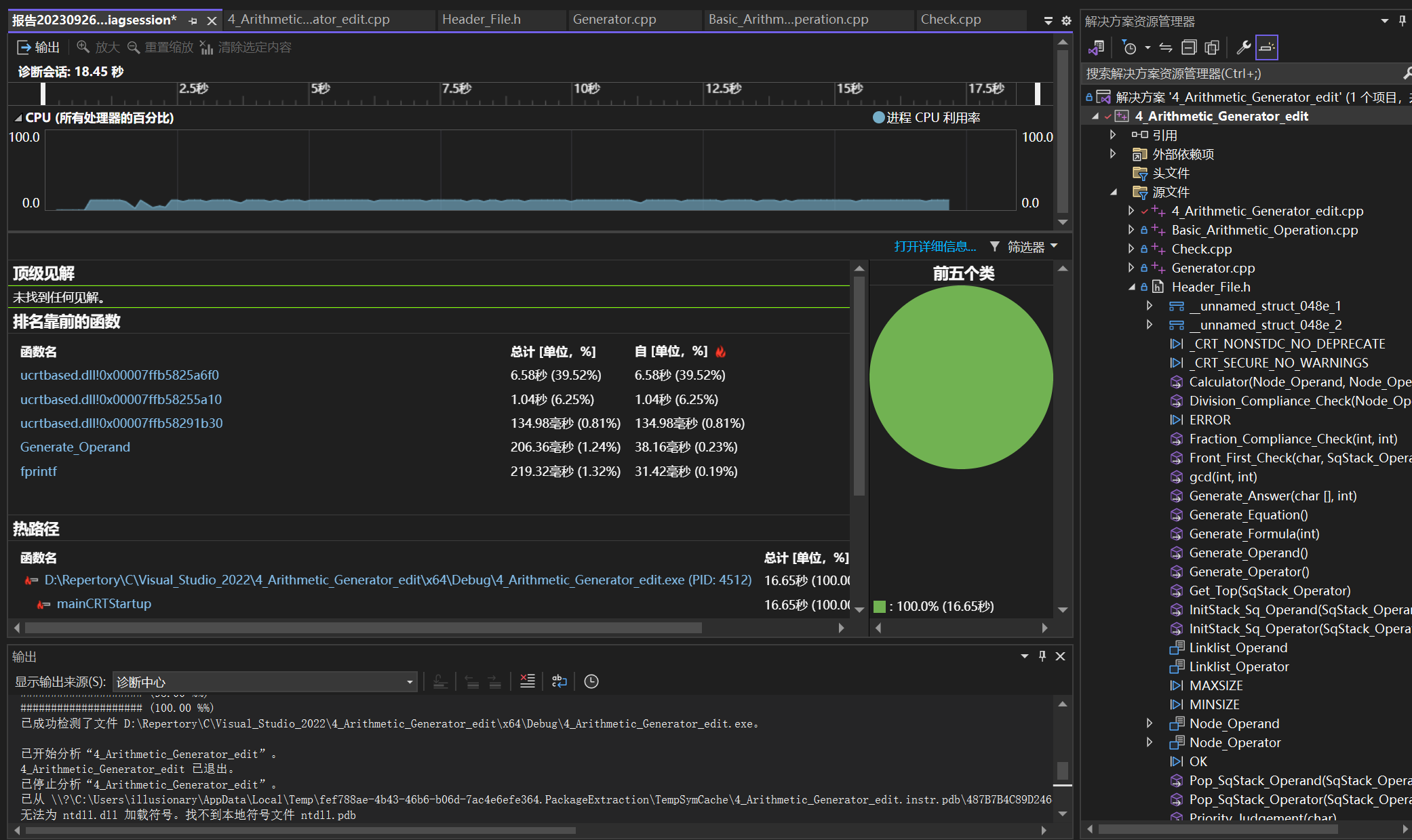
热力图
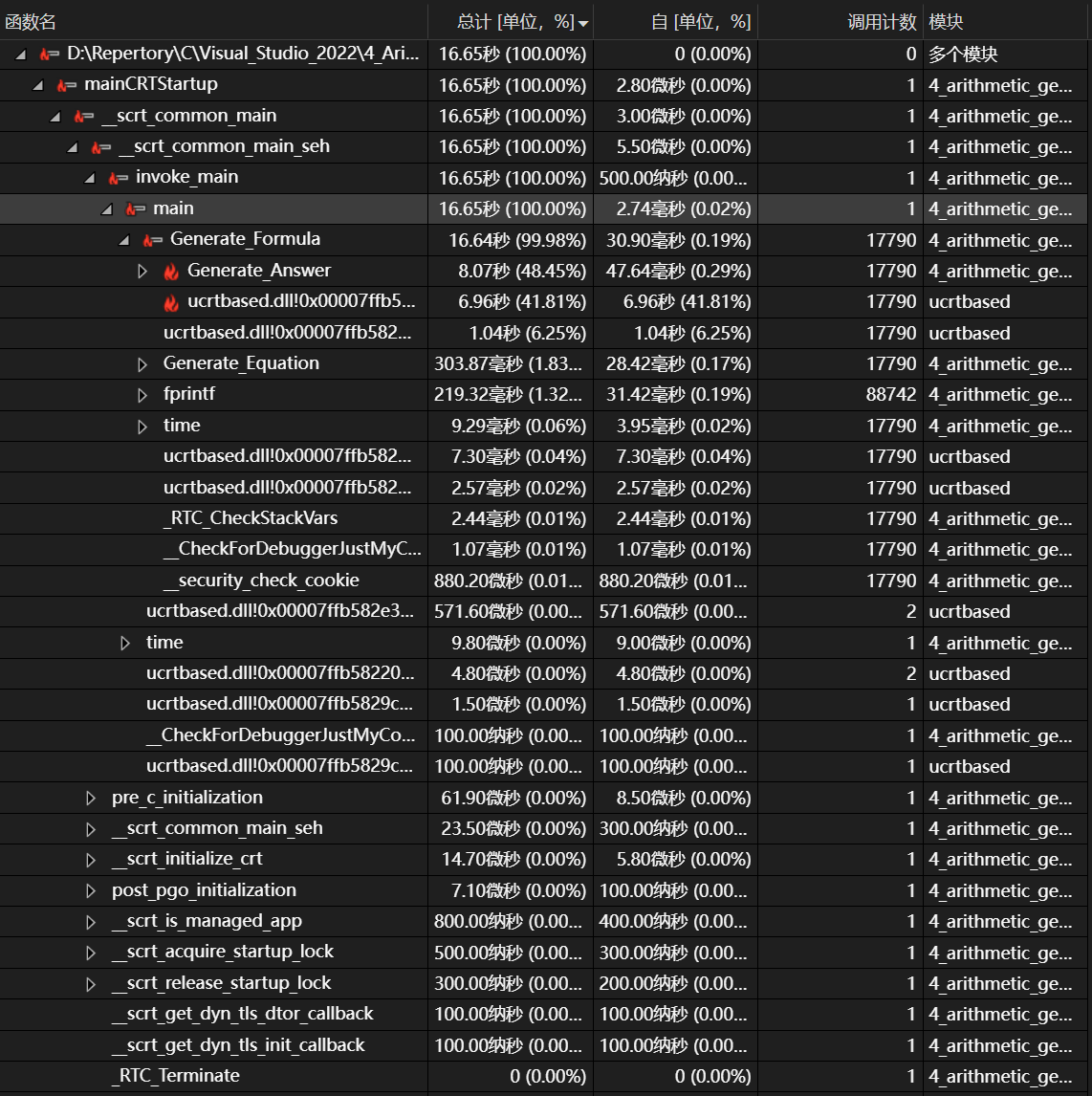
火焰图
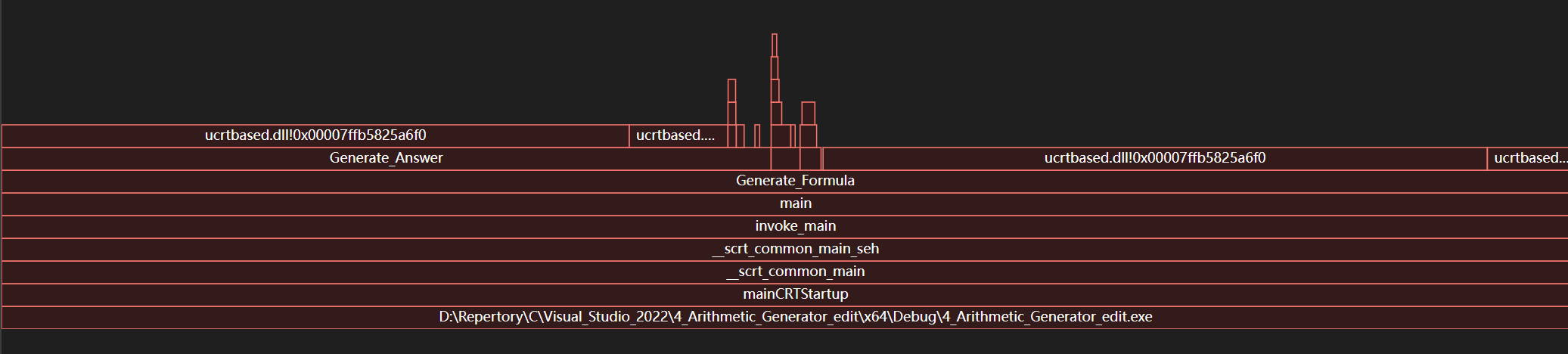
主要函数耗时占比
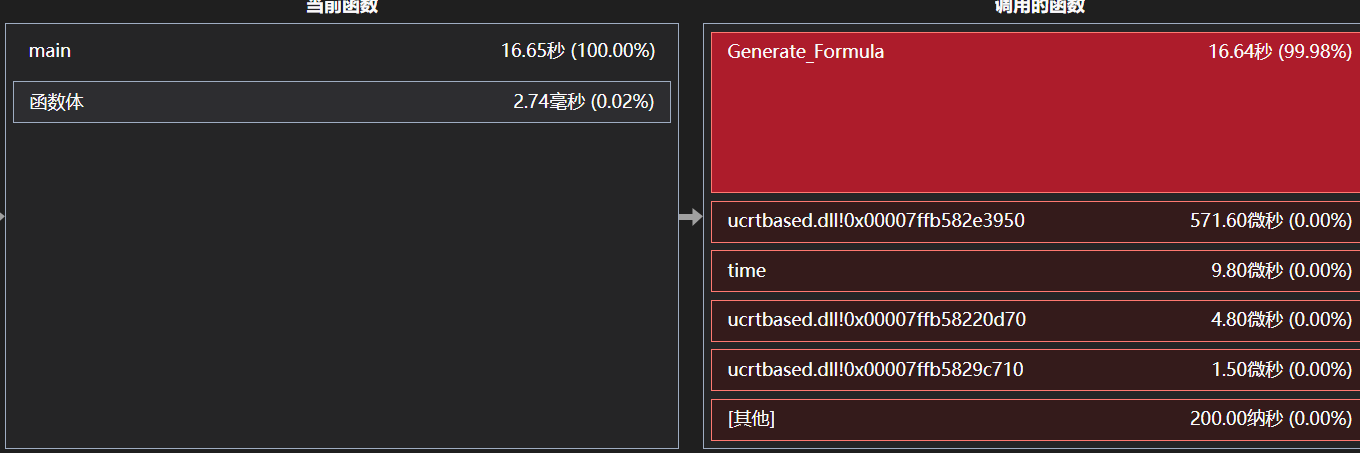
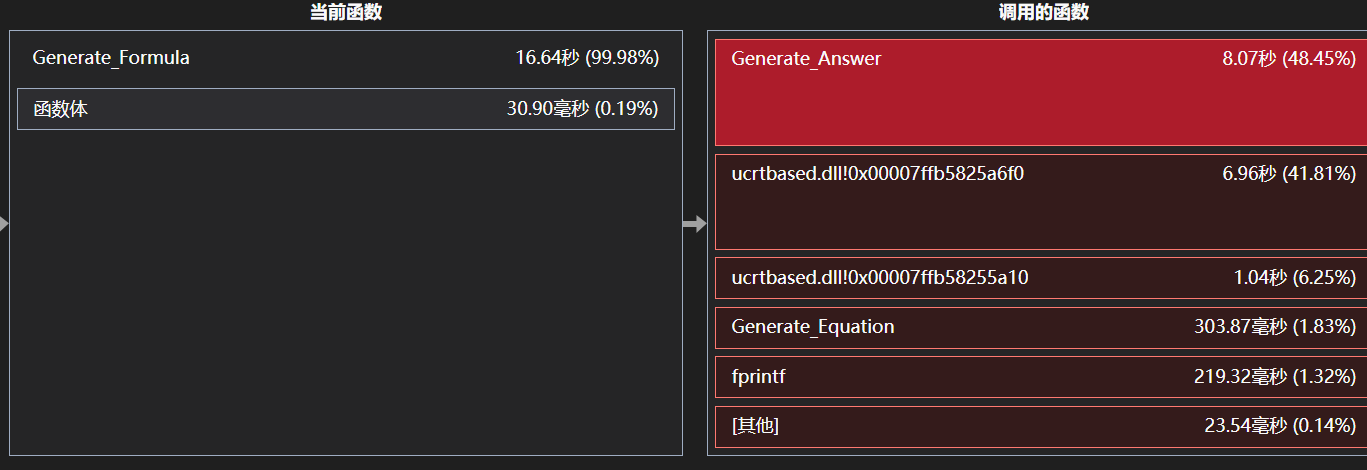
可见Generate_Fomula函数中调用的Generate_Answer函数耗时较大,有优化空间。
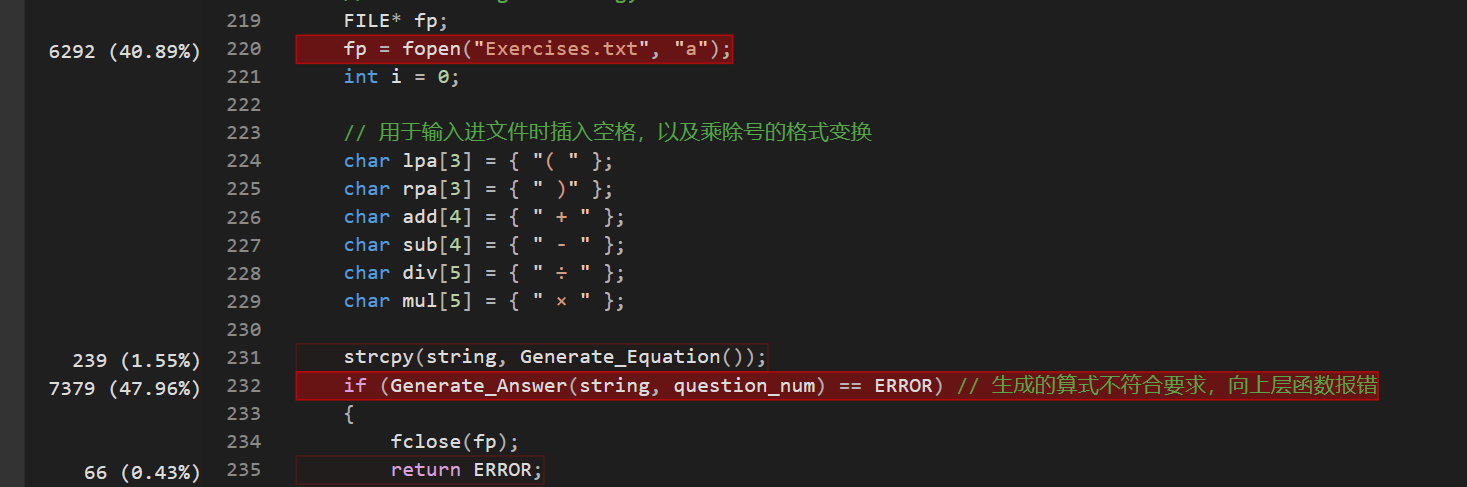
而Generate_Answer函数之所以被调用多次,是因为生成的大多数算式不符合题目要求,导致需要重新生成大量新算式。因此生成算式的逻辑有较大提升空间。
六、单元测试
测试结果
-n 10 -r 10


-n 10000 -r 10
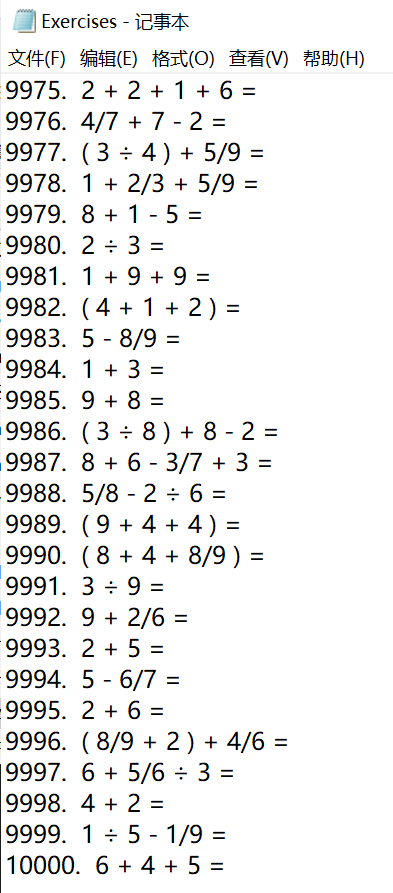

七、异常处理
命令行参数输入错误

八、项目小结
项目局限性
1、总体框架结构不够清晰,部分函数在功能上存在交集
2、生成的算式中不符合题意的居多,导致程序需要花大量时间于生成新算式
改进方法
1、将部分相似的函数功能进行合并,而同一函数中功能差异较大的部分可以单独提出,形成一个新函数
2、改进算式生成的逻辑,使其在第一遍就尽可能生成符合题意的算式,尽量避免为了生成一条符合题意的算式而生成大量不符合题意的算式的情况
个人收获
1、对软件设计流程有了初步的了解。拿到新项目时,能够先从需求分析入手,设计顶层,设计各个功能模块,进而设计所需要的数据结构,厘清各函数之间的调用关系,最后进行编码。
2、代码编写速度有了一定的提升





 浙公网安备 33010602011771号
浙公网安备 33010602011771号