PAC Learning 学习笔记

#计算学习理论

前置知识

Hoeffding 不等式

设 \(X_1, X_2, \cdots, X_n\) 是独立随机变量，其中 \(X_i \in [a_i, b_i]\)，令 \(S_n = \sum_{i=1}^n X_i\)，

那么

\[\mathbb{P}(S_n - \mathbb{E}[S_n] \geq t) \leq \exp\left\{-\frac{2t^2}{\sum_{i=1}^n (b_i - a_i)^2}\right\} \]

Proof:

Hoeffding 引理：设 \(X \in [a, b]\)，\(\mathbb{E}[\exp\{t(X-\mathbb{E}X)\}] \leq \exp\{\frac{t^2(b-a)^2}8\}\)。

proof sketch：根据凸性，左端最大值在 \(X\) 是 \(\{a, b\}\) 的两点分布时取到。此时，\(M_{X-\mathbb{E}X}(t) = \cosh (t(\frac{b-a}2))\)，根据 \(\cosh x \leq e^{\frac{x^2}2}\) 可得结果。

\[\begin{aligned} \mathbb{P}(S_n - \mathbb{E}[S_n] \geq t) &= \mathbb{P}(M_{S_n-\mathbb{E}[S_n]}(s) \geq e^{st}) \\ &\leq e^{-st}\mathbb{E}[M_{S_n - \mathbb{E}[S_n]}(s)] & \text{(Markov不等式)}\\ &= e^{-st} \prod_{i=1}^n \mathbb{E}[M_{Y_i}(s)] & Y_i=X_i-\mathbb{E}X_i\\ &\leq e^{-st} \prod_{i=1}^n \exp\left\{\frac{s^2 (b_i - a_i)^2}{8}\right\} & \text{Hoeffding引理} \\ &= \exp\left\{\frac18\sum_{i=1}^n(b_i-a_i)^2 s^2 -st\right\} \\ &\leq \exp\left\{-\frac{2t^2}{\sum_{i=1}^n (b_i - a_i)^2}\right\} & \text{关于} s \text{二次函数最小值} \end{aligned} \]

推论：考虑独立同分布变量 \(X_1, \cdots, X_n\)，并且 \(X_i \in [0, 1]\)，那么有：

\[\mathbb{P}(\overline{X} - \mathbb{E}[\overline{X}] \geq \varepsilon) \leq \exp(-2n\varepsilon^2) \\ \mathbb{P}(|\overline{X} - \mathbb{E}[\overline{X}]| \geq \varepsilon) \leq 2 \exp(-2n\varepsilon^2) \]

McDiarmid 不等式

对于独立随机变量 \(X_1, \cdots, X_n\)，其中 \(f\) 满足：

\[\sup_{X_1, \cdots, X_n, X_i'} |f(X_1, \cdots, X_n) - f(X_1, \cdots, X_{i-1}, X_i', X_{i+1}, \cdots, X_n)| \leq c_i \]

则对于 \(\forall \varepsilon > 0\)，有

\[\mathbb{P}(f(X_1, \cdots, X_n) - \mathbb{E}[f(X_1, \cdots, X_n)]\geq \varepsilon^2) \leq \exp\{\frac{-2\varepsilon^2}{\sum_i c_i^2}\} \]

Proof Skech：首先 \(f(X)-\mathbb{E}f(X) =\sum_k D_k, |D_k| \leq c_k\)。（构造Doob条件期望列）。根据 Hoeffding 引理，\(\mathbb{E} [e^{t(f-\mathbb{E}f)}] \leq \exp(\frac{t^2}{8}\sum_k c_k^2)\)。后面证明同 Hoeffding 不等式（利用矩母函数和Markov不等式）。

PAC Learning（可能大致正确）

PAC可学习：一个问题，存在一个算法 \(A\)，对于任何分布 \(D\) 和任何概念 \(c\)，当给定大量独立的样本时，很有可能得到一个误差很小的对于 \(c\) 的假设（估计）。

例如：可以通过在平面内撒点，根据点是否在一个圆内，来估算圆的坐标半径。

Concept Classes 概念类

概念类 \(C\) 定义在集合 \(X\) 上，其中每一个概念 \(c \in C\) 都是一个 \(X \to \{ 0, 1\}\) 的函数。

查询函数，我们可以调用概念 \(c\) 对应的查询函数来观察采样到的样本的信息。

Probably Approximately Correct Learning

PAC learning 的目标是，找到一个算法，可以在通过采样随机样本，来作出良好的假设。这里的假设也是一个 \(X \to \{0, 1\}\) 的函数，用来拟合某个概念 \(c\)。

假设形成空间 \(\mathcal{H}\)(假设空间)，定义一个假设 \(h\) 的误差为 \(\mathrm{err}_{c,D}(h)\)，我们用误差来衡量假设的正确性，并设置良好假设的误差上限为 \(\varepsilon\)。

\[\mathrm{err}_{c, D}(h) = \mathbb{P}_{x \sim D}(h(x) \neq c(x)) \]

1. 高置信度：\(\mathbb{P}_D(\mathrm{err}_{c,D}(h) \leq \varepsilon) > 1 - \delta\)。
2. 复杂度可行：我们限制算法的时间和空间复杂度均为 \(O(\mathrm{poly}(\frac{1}{\varepsilon},\frac1{\delta}))\)。（完整情况还应考虑数据复杂度 \(\mathrm{size}(x)\) 和概念复杂度 \(\mathrm{size}(c)\)）。这个复杂度也被称作是样本复杂度（一般用来刻画需要的样本量 \(m\)）。

若该对于 \(\varepsilon, \delta \in [0, \frac12]\)，都存在满足条件的算法 \(A(\varepsilon, \delta)\)，则该问题是 PAC- Learnable 的。

区间是可学习的

\(\mathbb{R}\) 上区间是 PAC-learnable 的。

设 \(c(x) = \mathcal{X}_{[a_0, b_0]}\)，\(h(x) = \mathcal{X}_{[a_1, b_1]}\)，其中 \(a_1\) 是样本中属于区间的最小值，\(b_1\) 是最大值。

设采样分布为 \(D\)。则 \(\mathrm{err}_{c, D}(h) = \mathbb{P}(x \in (A=[a_0, a_1]) \cup (B=[b_1, b_0]))\)。

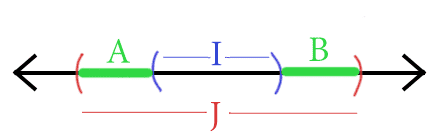
我们构造算法，使得 \(\mathbb{P}(A), \mathbb{P}(B) < \frac{\varepsilon}2\)。

具体的，定义 \(A' = [a_0, y]\)，满足 \(\mathbb{P}(A') = \frac{\varepsilon}2\)。

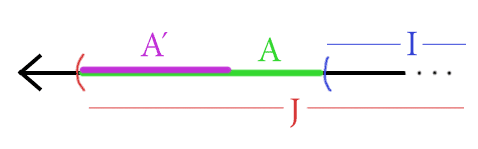
那么只要采样对 \(A'\) 中的点调用了查询函数，则 \(A \subseteq A'\) 。因此，

\[\mathbb{P}(A' \subset A) = (1 - \varepsilon/2)^m \]

类似地定义 \(B'\)。

\[\begin{aligned} \mathbb{P}_D(\mathrm{err}_{c, D}(h)) &> \mathbb{P}_D\left(\max(\mathbb{P}(A), \mathbb{P}(B)) < \frac{\varepsilon}2\right) \\ &= \mathbb{P}_D (A \subseteq A' \land B \subseteq B') \\ &> 1 - \mathbb{P}(A' \subset A) - \mathbb{P}(B' \subset B) \\ &= 1 - 2 (1 - \frac{\varepsilon}2)^m \\ &= 1 - 2e^{-\frac{\varepsilon m}2} \end{aligned} \]

所以当 \(m = \lceil \frac{2}{\varepsilon} \log (\frac{2}{\delta })\rceil \sim O(\mathrm{poly}(\frac1{\varepsilon},\frac1{\delta}))\) 时，上式成立。

有限假设空间

对应 \(|\mathcal{H}| < \infty\) 的情况。

Case1

若 \(c\in \mathcal{H}\)，称 \(\mathcal{H}\) 可分，此时可以通过不断剔除不对的假设，最后在样本集上表现完美的假设中随机选择一个。

考虑一个误差大于 \(\varepsilon\) 的假设在样本上表现完美的概率：\(\mathbb{P}[h(x_i)\equiv y_i] = (1 - \mathbb{P}(h(x)\neq y))^m \leq (1 - \varepsilon)^m\)

算法出错的概率小于存在一个上述假设的概率，设 \(k\) 表示 \(\mathcal{H}\) 中误差大于 \(\varepsilon\) 的假设的个数，那么出错概率小于 \(k \cdot (1-\varepsilon)^m < |\mathcal{H}| \cdot(1-\varepsilon)^m < |\mathcal{H}|e^{-m\varepsilon}\)。

所以 \(m \geq \frac1{\varepsilon} (\ln |\mathcal{H}| + \ln \frac1{\delta})\)。

Case2

若 \(c\notin \mathcal{H}\)，称 \(\mathcal{H}\) 不可分，此时有可能 \(\mathcal{H}\) 中的所有假设对于一个样本集都不是完美的。

记泛化误差为 \(E(h) = \mathrm{err}_{c, D}(h)\)，经验误差为样本集上的误差 \(\hat{E}(h) = \frac1m \sum_i \mathbb{I}_{h(x_i) \neq y_i}\)。我们考虑选择经验误差尽可能小的假设（即选择 \(\hat{E}(h)\) 最小的假设，该原则称作经验风险最小化(Empirical Risk Minimization/ERM)）。

考虑把 \(\mathbb{I}_{h(x_i) \neq y_i}\) 看成是独立同分布随机变量，根据 Hoeffding 不等式可得：

\[P(|E(h) - \hat{E}(h)| \geq \varepsilon) \leq 2 \exp(-2m\varepsilon^2) \]

直观上更大的样本集可以更好的反应总体的误差。

不可知PAC可学习（agnostic PAC learnable）

考虑逼近假设集中最小误差的假设，

\[\mathbb{P}(E(h) - \min_{h'\in \mathcal{H}}E(h') \leq \varepsilon) \geq 1 - \delta \]

定理：对于任意 \(h\in \mathcal{H}\)，有

\[P(|E(h) - \hat{E}(h)| \leq \sqrt{\frac{\ln |\mathcal{H}| + \ln(2/\delta)}{2m}}) \geq 1 - \delta \]

此时所有假设的经验误差一致收敛到泛化误差。因此此时是不可知PAC可学习的。

VC 维

在无限假设空间的情况下，我们使用假设空间的 VC 维来刻画一个假设空间的表达能力。

在有限的样本上，如果两个假设给出的结果完全相同，则认为它们等价。给定一个样本集 \(D\)，令 \(\mathcal{H}\mid_D\) 表示由 \(D\) 形成的等价类。

定义增长函数 \(\Pi_{\mathcal{H}}(m)\) 表示样本空间 \(\mathcal{X}\) 上所有大小为 \(m\) 的样本集 \(D\) 中 \(|\mathcal{H}\mid_D|\) 的最大值。

定理 对于假设空间 \(\mathcal{H}\)，\(m\in \mathbb{N}, \varepsilon \in [0, 1]\) 和任意 \(h\in \mathcal{H}\) 有

\[\mathbb{P}(|E(h) - \hat{E}(h)| > \varepsilon) \leq 4 \Pi_{\mathcal{H}}(2m) \exp(-\frac{m\varepsilon^2}{8}) \]

我们只考虑二分类的问题，定义一个假设空间的 VC 维是：

\[\mathrm{VC}(\mathcal{H}) = \max \{m : \Pi_{\mathcal{H}}(m) = 2^m\} \]

直观上是能“打散”的最大样本集大小。

VC维可以用于约束增长函数的大小。若假设空间 \(\mathcal{H}\) 的 VC 维（至多）为 \(d\)，则对于任意 \(m \in \mathbb{N}\) 有

\[\Pi_{\mathcal{H}}(m) \leq \sum_{i=0}^d \binom{m}{i} \]

证明考虑数学归纳法，当 \((m-1, d-1)\) 和 \((m-1, d)\) 成立时，对于任意大小为 \(m\) 的样本集合 \(D = \{x_1, x_2,\cdots, x_m\}\)。令 \(D' = \{x_1, \cdots, x_{m-1}\}\)。

考虑 \(\mathcal{H}\mid_{D'}\) 中的等价类在 \(\mathcal{H}\mid_D\) 中要么出现 \(1\) 次，要么出现 \(2\) 次，令 \(\mathcal{H}_{D'\mid D}\) 表示出现了 \(2\) 次的部分。其中 \(\mathcal{H}\mid_{D'}\) 关于集合 \(D'\) 的 VC 维至多为 \(d\)，而 \(\mathcal{H}_{D'\mid D}\) 关于 \(D'\) 的 VC 维至多为 \(d-1\)（因为加入 \(x_m\) 后可以让 VC 维多 \(1\)）。

\[\begin{aligned} |\mathcal{H}\mid_D| &= |\mathcal{H}\mid_{D'}| + |\mathcal{H}_{D'\mid D}| \\ &\leq \sum_{i=1}^d \binom{m-1}{i} + \sum_{i=0}^{d-1}\binom{m-1}{i} \\ &=\sum_{i=1}^d \binom{m-1}{i} + \binom{m-1}{i-1} \\ &= \sum_{i=0}^d \binom{m}{i} \end{aligned} \]

由此可以得到推论：\(\Pi_{\mathcal{H}}(m) \leq \sum_{i=0}^d \binom{m}{i} \leq \sum_{i=0}^d \binom{m}{i}(\frac{m}{d})^{d-i}\\=(\frac{m}{d})^d(1+\frac{d}{m})^m \leq (\frac{em}{d})^d\)

根据上述定理和增长函数的上界，最终可以得到以下定理（由此可知 VC 维有限时问题是 不可知PAC可学习的）。

定理 若 \(\mathcal{H}\) 的 VC 维是 \(d\)，则对任意 \(m > d, 0 < \delta < 1\) 和 \(h \in \mathcal{H}\) 有

\[P\left(\left|E(h) - \hat{E}(h)\right| \leq \sqrt{\frac{8d\ln \frac{2em}{d} + 8\ln \frac4{\delta}}{m}}\right)\geq 1 - \delta \]

因此，上述泛化误差界只与样本数量 \(m\) 有关，收敛速率为 \(O(\frac1{\sqrt m})\)，与数据分布和样本集合无关。基于 VC 维的泛化误差界是分布无关、数据独立的。

对于一个 VC 维有限的假设空间，设 \(h\) 是 ERM 输出的假设，\(g\) 是最优解。

通过设置 \(\sqrt{\frac{\ln 2/{\delta'}}{2m}} = \frac{\varepsilon}2\)，可得 \(\mathbb{P}(|\hat{E}(g) - E(g)| \leq \frac{\varepsilon}{2}) \geq 1 - \frac{\delta}2\)。

再设置 \(\sqrt{\frac{8d\ln \frac{2em}{d} + 8\ln \frac4{\delta}}{m}} = \frac{\varepsilon}{2}\)，可得 \(\mathbb{P}(E(h) - \hat{E}(h) \leq \frac{\varepsilon}{2}) \geq 1 - \frac{\delta}{2}\)。

因此 \(E(h) - E(g) \leq (\hat{E}(h) + \frac{\varepsilon}{2}) - (\hat{E}(g) - \frac{\varepsilon}{2}) \leq \hat{E}(h) - \hat{E}(g) + \varepsilon \leq \varepsilon\) 以至少 \(1-\delta\) 的概率成立。

Rademacher 复杂度

我们可以用 \(\frac1m\sum_{i=1}^m y_i h(x_i)\) 来刻画假设 \(h\) 关于样本集 \(D = \{(x_i, y_i)\}_{i=1}^m\) 的一致性。对于假设空间，直观上可以认为它能良好拟合的概念越多则越复杂，反过来，对于每个概念，假设空间里能找到的与其一致性最高的假设越好，则这个假设空间越能良好拟合出这个概念。

定义二值随机变量 \(\sigma_i\)，其中 \(\mathbb{P}(\sigma_i = 1) = \mathbb{P}(\sigma_i = -1) = \frac12\)。

那么我们可以用如下期望来反应一个假设空间的复杂度：

\[\mathbb{E}_{\sigma}\left[\sup_{h \in \mathcal{H}} \dfrac1m \sum_{i=1}^m \sigma_i h(x_i)\right] \]

基于此，我们将上述形式推广到更一般的函数空间（假设空间也是一种函数空间）。

定义 函数空间 \(\mathcal{F}: \mathcal{Z} \to \mathbb{R}\) 关于集合 \(Z = \{z_1, z_2, \cdots, z_m\} \subset \mathcal{Z}\) 的经验 Rademacher 复杂度为

\[\hat{R}_Z(\mathcal{F}) = \mathbb{E}_{\sigma} \left[\sup_{f\in \mathcal{F}} \frac1m \sum_{i=1}^m \sigma_i f(z_i)\right] \]

经验 Rademacher 复杂度可以描述在一个特定样本集上函数空间的表达能力。我们接着考虑样本的分布，对于从具有分布 \(\mathcal{D}\) 的空间 \(\mathcal{Z}\) 独立随机采样的样本集，我们定义函数空间的期望 Rademacher 复杂度。

定义 函数空间 \(\mathcal{F}\) 关于 \(\mathcal{Z}\) 上分布 \(\mathcal{D}\) 的 Rademacher 复杂度为

\[R_m(\mathcal{F}) = \mathbb{E}_{Z\subseteq \mathcal{Z} : |Z| = m} \left[\hat{R}_Z(\mathcal{F})\right] \]

与 VC 维不同的是，Rademacher 复杂度考虑了数据的分布情况，从两者式子可以看出，VC 维考虑“最好的样本集”，而 Rademacher 复杂度考虑的是选取样本集的平均情况。基于 Rademacher 复杂度同样可以得到泛化误差的上界。

定理 若 \(\mathcal{F} : \mathcal{Z} \to [0, 1]\)，对于从 \((\mathcal{Z}, \mathcal{D})\) 中 i.i.d 采样的样本集 \(Z=\{z_i\}_{i\le m}\) 和 \(\delta \in (0, 1)\)，以至少 \(1 - \delta\) 的概率有：对于任意 \(f \in \mathcal{F}\)，

\[\mathbb{E}[f(z)] \leq \frac1m\sum_{i\leq m} f(z_i) + 2 R_m(\mathcal{F}) + \sqrt{\frac{\ln(1/\delta)}{2m}} \tag{1} \]

\[\mathbb{E}[f(z)] \leq \frac1m\sum_{i\leq m}f(z_i)+2\hat{R}_Z(\mathcal{F}) + 3 \sqrt{\frac{\ln(2/\delta)}{2m}}\tag{2} \]

Proof Sketch: \(\hat{E}(f) = \frac{1}{m}\sum_{i\leq m} f(z_i)\)。

首先令 \(\Phi(Z) = \sup_{f\in \mathcal{F}} \mathbb{E}[f] - \hat{E}_Z(f)\)。考虑将 \(Z\) 中的 \(z_m\) 替换为 \(z_m'\) 变成 \(Z'\)。那么

\[\Phi(Z') - \Phi(Z) \leq \sup_{f\in \mathcal{F}} \hat{E}_Z(f) - \hat{E}_{Z'}(f) = \sup_{f\in \mathcal{F}}\frac{f(z_m) - f(z_m')}{m} \leq \frac1m \]

因此 \(|\Phi(Z) - \Phi(Z')| \leq \frac1m\)，根据 McDiarmid 不等式，对于 \(\forall \delta \in (0, 1)\)，

\[\Phi(Z) \leq \mathbb{E}_Z[\Phi(Z)] + \sqrt{\frac{\ln(1/\delta)}{2m}} \]

接下来还需要估计 \(\mathbb{E}_Z[\Phi(Z)]\) 的上界：

\[\begin{aligned} \mathbb{E}_Z[\Phi(Z)] &= \mathbb{E}_Z[\sup_{f\in \mathcal{F}} \mathbb{E}_{Z'}[\hat{E}_{Z'}(f) - \hat{E}_Z(f)]] \\ &\leq \mathbb{E}_{Z,Z'} [\sup_{f\in \mathcal{F}}\hat{E}_{Z'}(f) - \hat{E}_Z(f)] \\ &=\mathbb{E}_{Z,Z'} [\sup_{f\in \mathcal{F}}\frac1m\sum_{i\leq m}(f(z_i') - f(z_i))] \\ &=\mathbb{E}_{Z,Z',\sigma} [\sup_{f\in \mathcal{F}}\frac1m\sum_{i\leq m}\sigma_i(f(z_i') - f(z_i))] \\ &\leq 2\mathbb{E}_{Z,\sigma}[\sup_{f\in \mathbb{F}} \frac1m \sum_{i\leq m} \sigma_if(z_i)] \\ &=2R_m(\mathcal{F}) \end{aligned} \]

因此 \((1)\) 得证。根据 McDiarmid 不等式我们还可以知道以至少 \(1-\delta/2\) 的概率，我们有

\[\Phi(Z) \leq \mathbb{E}_Z[\Phi(Z)] + \sqrt{\frac{\ln(2/\delta)}{2m}} \\ \mathbb{E}_Z[\Phi(Z)] \leq 2R_m(\mathcal{F}) \leq 2(\hat{R}_Z(\mathcal{F}) + \sqrt{\frac{\ln(2/\delta)}{2m}}) \]

因此 \((2)\) 得证。

根据上述定理，可以得到在二分类问题上的推论。此时假设空间 \(\mathcal{H} : \mathcal{X} \to \{+1,-1\}\)，\(\mathcal{Z} = \mathcal{Z} \times \{+1, -1\}\)，定义 \(f_h(z) = \mathbb{I}(h(x) \neq y) \in [0, 1]\)。由此得到函数空间 \(\mathcal{F}_{\mathcal{H}}\)。

\[E(h) = \mathbb{E}[f]\\ \hat{E}(h) = \hat{E}(f) \\ \hat{R}_Z(\mathcal{F}_{\mathcal{H}}) = \mathbb{E}_{\sigma}\left[\sup_{h\in \mathcal{H}} \frac1m \sum_{i = 1}^m \sigma_i\frac{1-y_ih(x_i)}{2}\right] = \frac12 \hat{R}_D(\mathcal{H}) \\ R_m(\mathcal{F}_{\mathcal{H}}) = \mathbb{E}_Z \hat{R}_Z(\mathcal{F}_{\mathcal{H}}) = \frac12 \mathbb{E}_D[\hat{R}_D(\mathcal{H})] = \frac12 R_m(\mathcal{H}) \]

所以：

\[E(h) \leq \hat{E}(h) + R_m(\mathcal{H}) + \sqrt{\frac{\ln(1/\delta)}{2m}} \\ E(h) \leq \hat{E}(h) + \hat{R}_D(\mathcal{H}) + \sqrt{\frac{\ln(2/\delta)}{2m}} \]

定理 假设空间 \(\mathcal{H}\) 的 Rademacher 复杂度 \(R_m(\mathcal{H})\) 与增长函数 \(\Pi_{\mathcal{H}}(m)\) 满足

\[R_m(\mathcal{H}) \leq \sqrt{\dfrac{2\ln \Pi_{\mathcal{H}}(m)}{m}} \]

又因为 \(\Pi_{\mathcal{H}}(m) \leq (\frac{em}{d})^d\)。所以

\[E(h) \leq \hat{E}(h) + \sqrt{\frac{2d\ln\frac{em}{d}}{m}} + \sqrt{\frac{\ln(1/\delta)}{2m}} \]

稳定性

VC 维的分析和 Rademacher 分析都没有考虑具体的学习算法。

我们用“稳定性”来衡量算法在输入变化时的结果变化。用 \(\mathfrak{L}_D\) 来表示在训练集 \(D\) 上学到的算法。

用 \(D^{\backslash i}\) 表示去掉第 \(i\) 个样本的样本集，用 \(D^i\) 表示替换第 \(i\) 个样本的样本集。

定义损失函数 \(\ell : \mathcal{Y} \times \mathcal{Y} \to \mathbb{R}^+\)。

算法的泛化损失：\(\ell(\mathfrak{L}, \mathcal{D}) = \mathbb{E}_{x,y} [\ell(\mathfrak{L}_D(x), y)]\)

算法的经验损失：\(\hat{\ell}(\mathfrak{L}_D) = \frac1m\sum_{i=1}^m \ell(\mathfrak{L}_D(x_i), y_i)\)

留一损失（leave-one-out）：\(\ell_{loo}(\mathfrak{L}_D) = \frac1m\sum_{i=1}^m \ell(\mathfrak{L}_{D^{\backslash i}}, z_i)\)

若对于任意 \(x\in \mathcal{X}, z = (x, y), i = 1, \dots, m\)，一致的有 \(|\ell(\mathfrak{L}_D, y) - \ell(\mathfrak{L}_{D^{\backslash i}}, y)| \leq \beta\)，称算法关于损失函数 \(\ell\) 满足 \(\beta\)-均匀稳定性。此时显然也满足：\(|\ell(\mathfrak{L}_D, y) - \ell(\mathfrak{L}_{D^{i}}, y)| \leq \beta\)。

定理 给定从 \(\mathcal{D}\) 上独立随机采样的大小为 \(m\) 的样本集，若算法 \(\mathfrak{L}\) 满足 \(\beta\)-均匀稳定性，损失函数上界为 \(M\)，那么对于 \(m\geq 1, \delta \in (0, 1)\)，以至少 \(1 - \delta\) 的概率有：

\[\ell(\mathfrak{L}, \mathcal{D}) \leq \hat{\ell}(\mathfrak{L}, D) + 2\beta + (4m\beta + M)\sqrt{\frac{\ln(1 / \delta)}{2m}} \\ \ell(\mathfrak{L}, \mathcal{D}) \leq \ell_{loo}(\mathfrak{L}, D) + \beta + (4m\beta + M)\sqrt{\frac{\ln(1 / \delta)}{2m}} \\ \]

因此经验损害-泛化损失的差的收敛率为 \(O(\beta\sqrt{m})\)，当 \(\beta\) 较小时，收敛率越好。

定理 若学习算法 \(\mathfrak{L}\) 是 ERM 且稳定的，则假设空间 \(\mathcal{H}\) 可学习。

Proof Sketch：令 \(g\) 是最小泛化损失假设，取 \(\frac{\delta}2 = 2\exp(-2m(\varepsilon')^2)\)。

根据 Hoeffding 不等式：当 \(m \geq \frac2{\varepsilon^2}\ln \frac4{\delta}\) 时，\(|\ell(g, \mathcal{D}) - \hat{\ell}(g, D)| \leq \frac{\varepsilon}2\) 以至少 \(1 - \delta/2\) 的概率成立。

取 \(\beta = \frac1m\)，则取

\[\ell(\mathfrak{L}, \mathcal{D}) \leq \hat{\ell}(\mathfrak{L}, D) + \frac2m + (4 + M)\sqrt{\frac{\ln(1/\delta)}{2m}} = \hat{\ell}(\mathfrak{L}, D) + \frac{\varepsilon}{2} \]

解得 \(m = O(\frac1{\varepsilon^2}\ln\frac{1}{\delta})\)。所以，

\[\ell(\mathfrak{L}, \mathcal{D}) - \ell(g, \mathcal{D}) \leq \hat{\ell}(\mathfrak{L}, D) + \frac{\varepsilon}2 - (\hat{\ell}(g, D) - \frac{\varepsilon}2) \leq \varepsilon \]

以至少 \(1-\delta\) 的概率成立。

可以看出稳定性不仅仅依赖算法，也与假设空间有关。

参考链接

【1】https://www.jeremykun.com/2014/01/02/probably-approximately-correct-a-formal-theory-of-learning/

【2】周志华《机器学习》第12章：计算学习理论

【3】https://zhuanlan.zhihu.com/p/344386947

【4】https://zhuanlan.zhihu.com/p/578316987