教训
-
树上背包强烈建议把循环 son 放在最外层,并且动态更新 size。(其实好像不必)
-
使用滚动数组的时候一定要看一眼简化后的状态转移方程。比方说 \(dp[t][now][k] = \max(dp[t - 1][now][j] + dp[sz[son]][son][k - j])\),滚掉 t 之后变成 \(dp[now][k] = \max(dp[now][j] + dp[son][k - j])\)。写代码的时候我们会写成用 \(dp[now][j] + dp[son][k - j]\) 与 \(dp[now][k]\) 取 \(\max\),但这会导致 \(dp[now][k]\) 单调不降。如果设的状态不是这个意思的话,一定不能这么写,可以考虑写成 \(dp[2][now][k]\)。
-
树上背包循环的范围记得要和当前节点的 size 取 min,否则的话复杂度不对。(是通过在 LCA 处贡献复杂度的方法来证明复杂度的)
-
树上背包第二层 for 建议循环跟当前根节点有关的那一部分,就是说 \(dp[now][k] = \max(dp[now][j] + dp[son][k - j])\) 这样的方程,第二层 for 循环 j 而不是 k - j。这是因为状态转移时要保证 \(dp[now][j]\) 用的是上一层的值,但如果循环的是 k - j 的话就有可能当 k - j 为 0 时用这一层的 dp 值去更新。但这个时候要注意循环的范围是和 \(sz[now] - sz[son]\) 取 min。(这个 \(sz[now]\) 指的是动态更新到的 sz)
-
树上背包初始化的时候就当成只有当前节点那一个点初始化即可,往后一步步把子树加入。
- 不要出现 UB!否则的话本来数组越界该显示 RE 就可能显示成 MLE。
P3605 [USACO17JAN]Promotion Counting P
- 树上启发式合并写的时候要注意不要再计算子树答案之前就把当前根节点加入,否则会出大问题。
- 同时要注意一个节点可能被访问多次,但只有第一次访问的时候数据结构中是它要的点,所以传一个 \(updans\),每次访问时结合当前节点的 \(updans\) 和要访问的节点的类型来确定 \(updans\)。
- 当然我这么写很麻烦,另一种方法是在第二轮遍历轻重儿子的时候直接按 \(dfs\) 序把它们全加进来,删除也类似,似乎更好一些。
P2857 [USACO06FEB]Steady Cow Assignment G
- 网络流注意 \(etot := -1,head[u] := -1\)。判断时用 \(i != -1\)。
- 注意 \(n,m\) 的意义是否正确,建议开 \(fn,fm,fs,ft\) 表示网络流的 \(n,m,s,t\),并在网络流中注意使用。
- 注意双向建边二倍空间。
- 关于这类有关割点或者点双连通分量的问题,一定要注意根节点的特殊考虑。
-
对于这种离散化之后覆盖的这种问题要格外小心,考虑如下这组数据:
-
in: 5 3 2 4 1 2 4 5 ans: 3 -
发现 3 根本没有在输入中出现,所以离散化的时候也不会去算进来它,而到后来把 2 和 4 覆盖掉之后,第一条线段相当于消失了。
-
这里我们注意,离散化过后每条线段相当于只覆盖了离散化之后的点,所以我们需要加一些点来描述线段的存在。
-
考虑在离散化的排序去重之后,在每一个数后面再加上一个比它大 1 的数,然后再次排序去重离散化,可以发现这样就解决了问题。
题意自己看一下。
状态:\(dp[i][dep]\) 表示 \(i\) 子树内选的最浅点相对深度 \(\ge dep\) 的最大权值和。
方程: \(dp[i][dep] = \max(dp[i][dep],dp[to][dep - 1] + \sum_{v \in son(i)-to}dp[v][\max(dep - 1,k - dep - 1)])(dep \not= 0)\)。
官方题解中说我们第一次求出的 \(dp[i][dep]\) 指的是最浅点正好是 \(dep\) 的。为什么是这样?我们在转移方程中用的 \(dp\) 指的不都是 \(\ge\) 吗?其实我觉得题解的说法不准确,求出的 \(dp[i][dep]\) 指的并不是最浅点是 \(dep\),而是指选定的最浅点深度 \(\ge dep\),其余的子树内的节点 \(\ge \max(dep - 1,k - dep - 1)\),发现了吧,在这种方程下即使你选中的最浅点深度 \(=h> dep\),其他节点还要满足与它自身要求不同的性质 (它自身需要 \(\ge \max(h - 1,k - h - 1)\) )。所以我们最后还得求一遍后缀最大值。
接下来,可以对比地来看一下以下几份提交:
首先我们来看一下错误版本错在哪里。
其实是个很简单的错误:考虑 \(now\) 子树内选取 \(to\) 作为最浅点,这个时候如果选取的相对深度很小(比方说 \(1\)),那么此时考虑将 \(v\) 子树合并进来,\(v\) 子树内选择的点到 \(v\) 的相对深度是有可能超过 \(k\) 的。
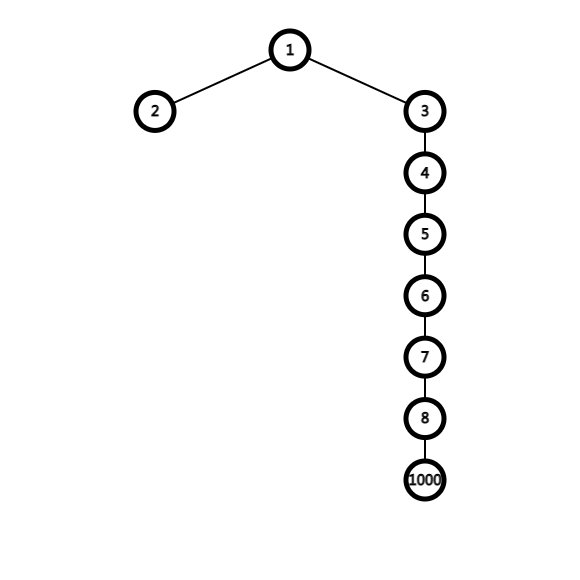
比方说这个图,\(k=4,now=1,to=2,v=3\),编号代表点权,这时可以发现 \(v\) 子树内最优选择就是只选择点 \(1000\),而 \(1000\) 与 \(3\) 的相对深度显然是比 \(k\) 要大的。而错误版本中计算只到 \(k\),所以有问题。
正确版本1的修改方法是把所有 \(f\) 改成 \(dp\),这样的话比方说在计算 \(dp[3]\) 的时候上图的情况就可以考虑进去。
正确版本2的修改方法是把循环范围从 \(k\) 改到 \(n\),这个好理解。
说了这么多,感觉似乎还是不太理解这道题,慢慢想吧。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号