模拟54 考试总结

考试经过

啥也不会，搞了N+1年T3无果，还有一个文件写错了，直接爆炸

T1.选择

观察到奇怪性质：每个点最多有10条边，这启发我们一些诸如枚举出边的复杂度是正确的
大框架还是一个dfs，用树型dp的方法统计答案，由于\(n^2\)是正确的，所以考虑枚举
对于一个点\(x\)，他的收益就是子树收益之和加上跨过\(x\)的点对收益
对每个点保存一个集合，表示他的子树中可以延伸到他的节点，初始化为自身，对于\(x\)枚举子树\(y1,y2\)，再暴力枚举\(y1,y2\)的所有子结点（不仅仅是直接儿子），如果给出输入有边相连则有\(link_{y1,y2}=1\)
然后显然可以状压，对边做，注意特殊处理直接到\(x\)的情况，做完就能算出\(x\)点的最大收益
然后分别考虑删除每个子树\(y\)，看答案是否有改变，如果没有那么能延伸到\(y\)的点都能延伸到\(x\) ，暴力合并即可
我的做法是每次重新做一边状压，由于每个点只会在他的父亲处统计，所以总共是均摊\(n^2\)的
当然也可以保存状态之类，然后每个点只做一次

#include <bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	int x=0;char ch=getchar();
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
const int N=1050;
struct node{
	int from,to,next;
}a[2*N];
int head[N],mm=1;
inline void add(int x,int y)
{
	a[mm].from=x;a[mm].to=y;
	a[mm].next=head[x];head[x]=mm++;
}
bool v[N],ps[N][N],l[N][N];
int ans[N],fa[N],size[N],son[N][12];
void dfs(int x)
{
	v[x]=1;int tot=0;
	for(int i=head[x];i;i=a[i].next)
	{
		int y=a[i].to;
		if(v[y])continue;
		fa[y]=x;size[x]++;
		son[x][++tot]=y;
		dfs(y);	
	}
}	
vector <int> t[N],sta[12];
inline int getsum(int x)
{
	int s=0;
	while(x)
	{
		if(x&1)s++;
		x>>=1;
	}
	return s;
}
int f[1<<12];
void dfss(int x,int ff)
{
	int tot=0;
	for(int i=head[x];i;i=a[i].next)
	{
		int y=a[i].to;if(y==ff)continue;
		dfss(y,x);ans[x]+=ans[y];
	}
	for(int i=head[x];i;i=a[i].next)
	{	
		int y=a[i].to;if(y==ff)continue;
		for(int ii=a[i].next;ii;ii=a[ii].next)
		{
			int yy=a[ii].to;
			if(yy==ff)continue;
			for(int k=0;k<t[y].size();k++)
			 for(int p=0;p<t[yy].size();p++)
			  if(ps[t[y][k]][t[yy][p]])l[y][yy]=1;
		}
		for(int k=0;k<t[y].size();k++)
		 if(ps[t[y][k]][x])l[y][x]=1;
	}
	memset(f,0,sizeof(f));
	for(int i=0;i<size[x];i++)
	{
		for(int j=0;j<sta[i].size();j++)
		{
			int s=sta[i][j];
			for(int k=1;k<=size[x];k++)
			{
				if((s>>(k-1))&1)continue;
				for(int p=1;p<=size[x];p++)
				{
					if(p==k)continue;
					if((s>>(p-1))&1)continue;
					f[s|(1<<(k-1))|(1<<(p-1))]=max(f[s|(1<<(k-1))|(1<<(p-1))],f[s]+l[son[x][k]][son[x][p]]);
				}
				f[s|(1<<(k-1))]=max(f[s|(1<<(k-1))],f[s]+l[son[x][k]][x]);
			}
		}
	}
	int an=0;for(int i=1;i<(1<<size[x]);i++)an=max(an,f[i]);ans[x]+=an;
	for(int y=1;y<=size[x];y++)
	{
		memset(f,0,sizeof(f));
		for(int i=0;i<size[x];i++)
		{
			for(int j=0;j<sta[i].size();j++)
			{
				int s=sta[i][j];
				if((s>>(y-1))&1)continue;
				for(int k=1;k<=size[x];k++)
				{	
					if(k==y)continue;
					if((s>>(k-1))&1)continue;
					for(int p=1;p<=size[x];p++)
					{
						if(p==k||p==y)continue;
						if((s>>(p-1))&1)continue;
						f[s|(1<<(k-1))|(1<<(p-1))]=max(f[s|(1<<(k-1))|(1<<(p-1))],f[s]+l[son[x][k]][son[x][p]]);
					}
					f[s|(1<<(k-1))]=max(f[s|(1<<(k-1))],f[s]+l[son[x][k]][x]);
				} 
			}
		}
		int ann=0;for(int i=1;i<(1<<size[x]);i++)ann=max(ann,f[i]);
		if(ann==an)for(int i=0;i<t[son[x][y]].size();i++)t[x].push_back(t[son[x][y]][i]);
	}
}
signed main()
{
	freopen("select.in","r",stdin);
	freopen("select.out","w",stdout);
	int n=read();
	for(int i=1;i<n;i++)
	{
		int x=read(),y=read();
		add(x,y);add(y,x);
	}
	int m=read();
	for(int i=1;i<=m;i++)
	{
		int x=read(),y=read();
		ps[x][y]=ps[y][x]=1;
	}
	dfs(1);memset(v,0,sizeof(v));
	for(int i=1;i<=n;i++)t[i].push_back(i);
	for(int i=0;i<(1<<10);i++)sta[getsum(i)].push_back(i);
	dfss(1,0);cout<<ans[1]<<endl;
	return 0;
}

T2.表格

对于三个格子的情况有以下几种

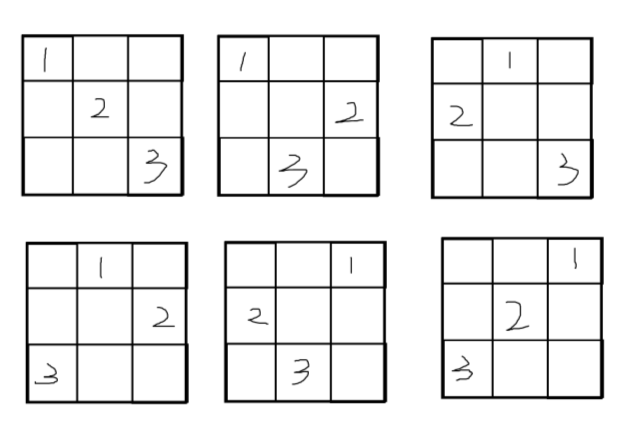
所以只要统计一种的答案再乘6就行
对于上下界显然可以差分，就变成了只有\([1,lim]\)的限制，先放式子

\[\sum_{i=3}^n(i-2)\times (n-i+2) \sum_{j=3}^{\min (m,\lfloor lim/2\rfloor-i+2)}(j-2)\times (m-j+2) \]

这里只算第一种，那么\(n,m\)就是枚举矩形的长和宽，\((i-2)\times (j-2）\)是中间一个点放的方法（钦定两个点一定在角上），\((n-i+2)\times (m-j+2)\)是整个格子里有多少个这样的矩形，保证不重不漏
然而范围有足足\(10^{18}\)，肯定不能枚举，考虑快速算
将它们换成多项式的形式，然后高斯消元(拉格朗日插值)就能算，因为还不会就咕了

T3.黑白

正解SG函数，咕了

T4.打怪

凸包送命题，貌似贪心可过但是被hack了，咕

考试总结

要正确给题定位，考试时肝了T3而没怎么看最可搞的T2，选好策略