模拟50 考试总结

只要你相信你能卡过，你就能卡过 ——班长

考试经过

T1第一眼：树剖板子？ 上来开冲，然后发现过不了样例。。。
果断开始打暴力，T2是个dp，只会智障部分分，T3想了一下可以bfs，八点多冲完了开始想正解
然而根本不会正解…… 发现T1暴力假了，修了一遍，部分分也没想法。。。
40+20+20=80 这能水到rk10。。。
T1暴力可过，T3暴力可过，\(chuxiaoxiao\) 220rk1%%%
一直对部分分开数组，数据这么水我也是没想到的

T1. 第零题

题目名好评
要知道一个性质是对于一条路径，如果满血开始走，从两端开始复活次数都是一样的
证明：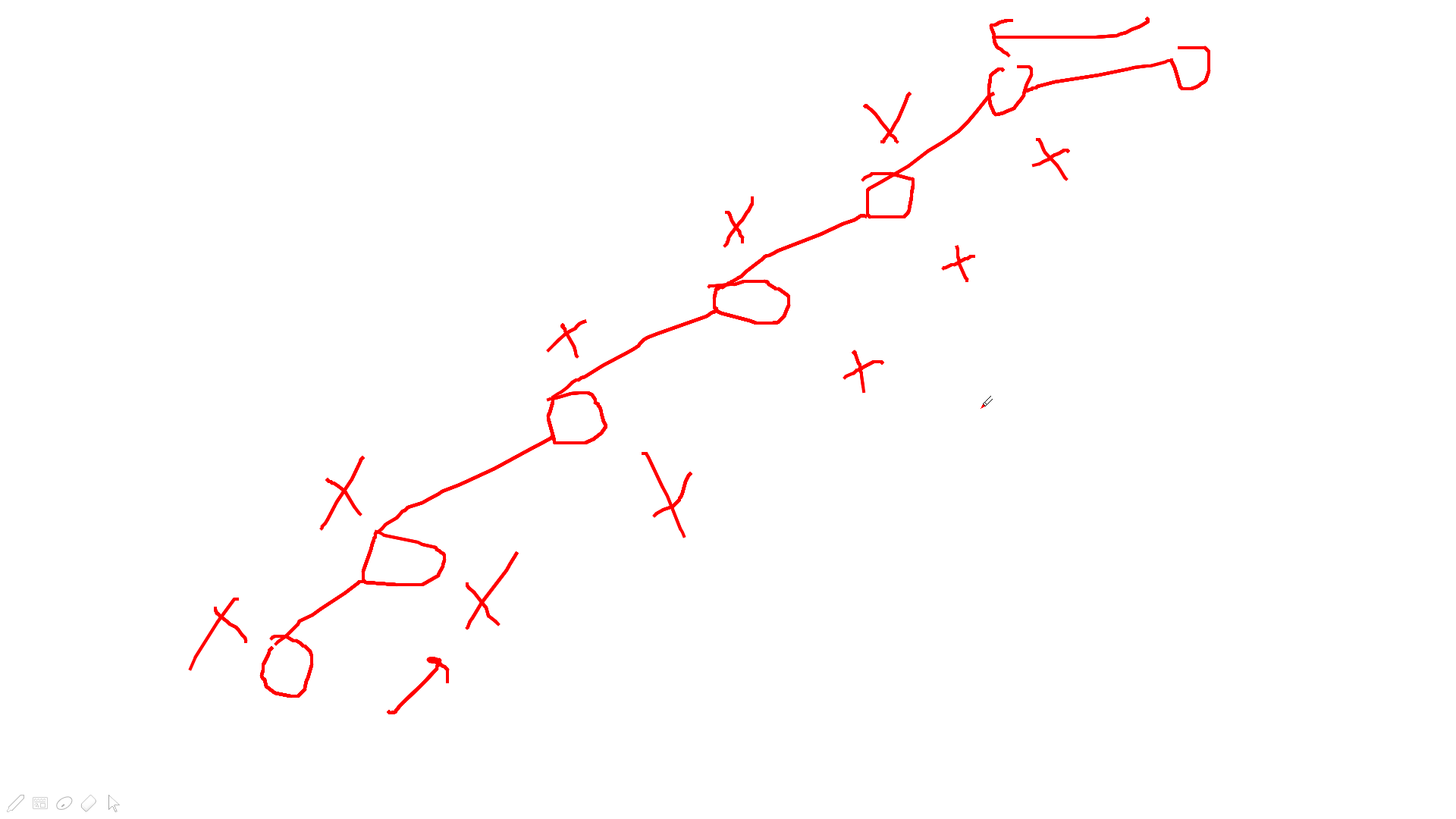
假如你要从下往上走，标记的点都是你要死的点（可能中间还有点但是不会死），那么你每往上走一次会死，最后你残血但不死，现在你反过来从上往下走，走到第一个点不会死，但到下一个点之前一定会死且仅死一次，然后你又残血，最后发现次数是一样的
顺便有一个更重要的结论，就是发现中间一段重复了，事实上如果有一段路从满血开始走最后恰好在终点死掉，那么可以直接统计复活次数而不用关心路径长度，所以这个题就简单了
从根dfs可以求出一个点到他祖先的路径长度，倍增预处理出每个点向上的死亡点，再对死亡点倍增把两个点提到lca附近，然后看lca到他们的路径之和，如果大于\(k\)就多复活一次，全程倍增实现可以一个\(log\)

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=200050;
inline int read()
{	
	int x=0;char ch=getchar();
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return x;
}
struct node{
	int from,to,next,w;
}a[2*N];
int head[N],mm=1;
inline void add(int x,int y,int z)
{
	a[mm].from=x;a[mm].to=y;a[mm].w=z;
	a[mm].next=head[x];head[x]=mm++;
}
int n,k,t;
int d[N],fa[N][20],w[N];bool v[N];
void dfs(int x)
{	
	v[x]=1;
	for(int i=head[x];i;i=a[i].next)
	{	
		int y=a[i].to;
		if(v[y])continue;
		d[y]=d[x]+1;
		w[y]=w[x]+a[i].w;
		fa[y][0]=x;
		for(int j=1;j<=t;j++)
		 fa[y][j]=fa[fa[y][j-1]][j-1];
		dfs(y);
	}
}
int die[N][20],bit[23];
int getdie(int x)
{
	int sum=k;
	for(int i=t;i>=0;i--)
	{
		int f=fa[x][i];
		if(!f)continue;
		int p=w[x]-w[f];
		if(p<sum)
		{
			sum-=p;
			x=fa[x][i];
		}
	}
	return fa[x][0];
}
void dfss(int x)
{
	v[x]=1;
	for(int i=head[x];i;i=a[i].next)
	{
		int y=a[i].to;
		if(v[y])continue;
		die[y][0]=getdie(y);
		for(int j=1;j<=t;j++)
		 die[y][j]=die[die[y][j-1]][j-1];
		dfss(y);
	}
}
inline int getlca(int x,int y)
{
	if(d[x]>d[y])swap(x,y);
	for(int i=t;i>=0;i--)
	 if(d[fa[y][i]]>=d[x])y=fa[y][i];
	if(x==y)return x;
	for(int i=t;i>=0;i--)
     if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
	return fa[x][0]; 
}
inline int gan(int &x,int lca)
{	
	int ans=0;
	for(int i=t;i>=0;i--)
	{
		int f=die[x][i];
		if(!f)continue;
		if(d[f]>=d[lca])
		{
			ans+=bit[i];
			x=f;
		}
	}
	return ans;
}
signed main()
{	
	n=read(),k=read(),t=ceil((double)log(n)/log(2));
	bit[0]=1;for(int i=1;i<=20;i++)bit[i]=bit[i-1]*2;
	for(int i=1;i<n;i++)
	{
		int x=read(),y=read(),ww=read();
		add(x,y,ww);add(y,x,ww);
	}
	d[1]=1;dfs(1);
	memset(v,0,sizeof(v));dfss(1);
	int q=read();
	for(int i=1;i<=q;i++)
	{
		int s=read(),t=read();
		int lca=getlca(s,t);
		int ans=gan(s,lca)+gan(t,lca);	
		int ss=w[s]+w[t]-w[lca]*2;
		if(ss>k)ans++;
		printf("%lld\n",ans);
	}	
	return 0;
}

应该想到倍增的，关于结论觉得不妥就拍一下

T2.第负一题

分治好题，分成\(log\)个区间，对于每段统计经过区间中点的答案
分别考虑是否经过中点，两个dp数组 \(0/1\)代表是否经过\(mid\)的最大值
然后合并，对差值排序做前缀和，复杂度两个\(log\),细节和柿子咕了
建议观赏土哥博客，真的超清楚%%%

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
const int N=200050;
int a[N],f[2][N][2],g[2][N][2];
vector <int> s1,s2,s3;
inline bool cmp(int x,int y){return x>y;}
int solve(int l,int r)
{
	if(l==r)return a[l];
	int mid=(l+r)>>1;
	int ans=(solve(l,mid)+solve(mid+1,r))%mod;
	for(int i=l;i<=mid;i++)f[1][i][1]=f[1][i][0]=f[0][i][1]=f[0][i][0]=-1e15;
	for(int i=mid+1;i<=r;i++)g[1][i][1]=g[1][i][0]=g[0][i][1]=g[0][i][0]=-1e15;
	f[0][mid][0]=0;f[1][mid][1]=a[mid];
	for(int i=mid-1;i>=l;i--)
	{
		f[0][i][0]=max(f[0][i+1][1],f[0][i+1][0]);
		f[0][i][1]=f[0][i+1][0]+a[i];
		f[1][i][0]=max(f[1][i+1][1],f[1][i+1][0]);
		f[1][i][1]=f[1][i+1][0]+a[i];
	}
	g[0][mid+1][0]=0;g[1][mid+1][1]=a[mid+1];
	for(int i=mid+2;i<=r;i++)
	{
		g[0][i][0]=max(g[0][i-1][1],g[0][i-1][0]);
		g[0][i][1]=g[0][i-1][0]+a[i];
		g[1][i][0]=max(g[1][i-1][1],g[1][i-1][0]);
		g[1][i][1]=g[1][i-1][0]+a[i];
	}
	for(int i=l;i<=mid;i++)ans=(ans+(r-mid)*max(f[0][i][0],f[0][i][1])%mod)%mod;
	for(int i=mid+1;i<=r;i++)ans=(ans+(mid-l+1)*max(g[0][i][0],g[0][i][1])%mod)%mod;
	s1.clear();s2.clear();s3.clear();s2.push_back(1e15);
	for(int i=l;i<=mid;i++)s1.push_back(max((max(f[1][i][0],f[1][i][1])-max(f[0][i][0],f[0][i][1])),(int)0));
	for(int i=mid+1;i<=r;i++)s2.push_back(max((max(g[1][i][0],g[1][i][1])-max(g[0][i][0],g[0][i][1])),(int)0));
	sort(s1.begin(),s1.end());sort(s2.begin(),s2.end(),cmp);
	for(int i=0;i<s2.size();i++)
	{
		if(i==0)s3.push_back(s2[i]);
		else s3.push_back(s3[i-1]+s2[i]);
	}
	int p=s2.size()-1,sum=r-mid;
	for(int i=0;i<s1.size();i++)
	{	
		int x=s1[i];
		while(s2[p]<x&&p)p--;
		ans=(ans+s3[p]-(int)1e15+(sum-p)*x%mod)%mod;
	}
	return ans;
}
signed main()
{
	int n;cin>>n;
	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
	cout<<solve(1,n)<<endl;
	return 0;
}

这种题接触的少，不过质量不错，对于统计贡献啥的是一个重要的思考方向

T3.第负二题

真毒瘤。。。
\(n^2\)可以水过，不过被战神给的数据卡了

二分答案，判断\(k+1\)是否可行,等价于能不能放一个大小为\(k\)中心在当前行(记作\(i\))的菱形。

考虑中心\(y\)坐标的限制，那么对于任意\(j\)，有

\[y-(k-(j-i))>=l_j,y+(k-(j-i))<=r_j(i<=j<=i+k) \]

\[y-(k-(i-j))>=l_j,y+(k-(i-j))<=r_j(i-k<=j<=i) \]

化减一下就有

\[\max(\max(l_j+j+k-i),\max(l_j-j+k+i))<=y<=\min(\min(r_j-j-k+i),\min(r_j+j-k-i)) \]

\(k,i\)固定，我们只需要对\(l_j+j,l_j-j,r_j-j,r_j+j\)维护最值就好，可以RMQ每次\(O(1)\)

#include <bits/stdc++.h>
using namespace std;
#define ull unsigned long long
const int mod=998244353;
const int N=2000050;
ull random(ull &A, ull &B)
{ 
   ull T=A,S=B; 
   A=S;T^=T<<23; 
   T^=T>>17;T^=S^(S>>26); 
   B=T;return T+S; 
} 
void gen(int p,int L,int X,int Y,ull A,ull B,int l[],int r[]) 
{
   for(int i=1;i<=p;i++) 
   { 
      l[i]=random(A,B)%L+X; 
      r[i]=random(A,B)%L+Y; 
      if(l[i]>r[i])swap(l[i],r[i]); 
   } 
}
int l[N],r[N],bit[N],kk[N],n;
int f1[N][20],f2[N][20],f3[N][20],f4[N][20];
inline void pre()
{	
	for(int i=1;i<=n;i++)
	{
		f1[i][0]=l[i]-i;f2[i][0]=r[i]+i;
		f3[i][0]=l[i]+i,f4[i][0]=r[i]-i;		
	}	
	int t=log(n)/log(2)+1;
	for(int j=1;j<t;j++)
	 for(int i=1;i<=n-(1<<j)+1;i++)
	 {
	 	f1[i][j]=max(f1[i][j-1],f1[i+(1<<(j-1))][j-1]);
	 	f2[i][j]=min(f2[i][j-1],f2[i+(1<<(j-1))][j-1]);
	 	f3[i][j]=max(f3[i][j-1],f3[i+(1<<(j-1))][j-1]);
	 	f4[i][j]=min(f4[i][j-1],f4[i+(1<<(j-1))][j-1]);
	 }
}
inline int get1(int ll,int rr){int p=kk[rr-ll+1];return max(f1[ll][p],f1[rr-(1<<p)+1][p]);}
inline int get2(int ll,int rr){int p=kk[rr-ll+1];return min(f2[ll][p],f2[rr-(1<<p)+1][p]);}
inline int get3(int ll,int rr){int p=kk[rr-ll+1];return max(f3[ll][p],f3[rr-(1<<p)+1][p]);}
inline int get4(int ll,int rr){int p=kk[rr-ll+1];return min(f4[ll][p],f4[rr-(1<<p)+1][p]);}
inline bool check(int x,int i)
{
	if(i-x<=0||i+x>n||x*2+1>(r[i]-l[i]+1))return 0;
	int l1=get1(i,i+x)+i+x,r1=get2(i,i+x)-x-i;
   int l2=get3(i-x,i)+x-i,r2=get4(i-x,i)-x+i;
	if(max(l1,l2)<=min(r1,r2))return 1;
	return 0;
}
signed main()
{
	int L,X,Y;ull A,B;cin>>n>>L>>X>>Y>>A>>B;
	gen(n,L,X,Y,A,B,l,r);
	bit[0]=1;for(int i=1;i<=n;i++)bit[i]=1ll*bit[i-1]*3%mod;
	for(int i=1;i<=n;i++)kk[i]=log(i)/log(2);
	pre();int an=0;
	for(int i=1;i<=n;i++)
	{
		int ll=0,rr=n,ans;
		while(ll<=rr)
		{
			int mid=(ll+rr)>>1;
			if(check(mid,i))ans=mid,ll=mid+1;
			else rr=mid-1;
		}
		ans++;cout<<ans<<endl;
		an=(an+1ll*bit[i-1]*ans%mod)%mod;
	}
	cout<<an<<endl;
	return 0;
}

这样时空复杂度都是\(n\log n\),只有\(80\)，还要优化
发现每次\(f\)值变化只有1,所以只要判断\(x-1,x+1,x\)就行，进一步优化可以只用判断\(x,x+1\)，这样把二分优化掉
考虑优化RMQ，发现这个东西整体单调，可以单调队列
但这里细节极多，对于前两个单调队列，每次查询\([i-x,i]\)的最值，\(i\)每次增加1,如果先判断\(x+1\)，再判断\(x\)那么他是单调的没有问题
另外两个每次查询\([i,i+x]\)，这个东西不能保证一定单调，因为你如果直接判断的话会将\(x+1\)入队，如果这次答案是\(x-1\),下一个判断的时候会访问到不应该在队列里的元素，亲身调试2h心得。。。
正确做法是每次先不将后面的东西入队，而是先去队列中的最值，然后与后面的两个数取最值，等这一行的\(f\)最终确定之后再将该入队的入队，这样可以解决不完全单调的问题，算是一个魔改，复杂度\(O(n)\)

#include <bits/stdc++.h>
using namespace std;
#define ull unsigned long long
const int mod=998244353;
const int N=5000050;
ull random(ull &A, ull &B)
{ 
   ull T=A,S=B; 
   A=S;T^=T<<23; 
   T^=T>>17;T^=S^(S>>26); 
   B=T;return T+S; 
} 
void gen(int p,int L,int X,int Y,ull A,ull B,int l[],int r[]) 
{
   for(int i=1;i<=p;i++) 
   { 
      l[i]=random(A,B)%L+X; 
      r[i]=random(A,B)%L+Y; 
      if(l[i]>r[i])swap(l[i],r[i]); 
   } 
}
int l[N],r[N],f[N],bit[N],n;
int l1[N],l2[N],r1[N],r2[N];
deque <int> q1,q2,q3,q4;
inline int gan1(int ll,int rr)
{
	while(q1.size()&&q1.front()<ll)q1.pop_front();
	int ls=q1.size()?q1.back()+1:ll;
	for(int i=ls;i<=rr;i++)
	{
		while(q1.size()&&l1[q1.back()]<l1[i])q1.pop_back();
		q1.push_back(i);
	}
	return l1[q1.front()];
}
inline int gan2(int ll,int rr)
{
	while(q2.size()&&q2.front()<ll)q2.pop_front();
	int ls=q2.size()?q2.back()+1:ll;
	for(int i=ls;i<=rr;i++)
	{
		while(q2.size()&&r1[q2.back()]>r1[i])q2.pop_back();
		q2.push_back(i);
	}
	return r1[q2.front()];
}
inline int gan3(int ll)
{
	while(q3.size()&&q3.front()<ll)q3.pop_front();
	return q3.size()?l2[q3.front()]:-1e9;   
}
inline int gan4(int ll)
{
	while(q4.size()&&q4.front()<ll)q4.pop_front();
	return q4.size()?r2[q4.front()]:1e9;
}
inline void update3(int x)
{
	while(q3.size()&&l2[q3.back()]<l2[x])q3.pop_back();
	q3.push_back(x);
}
inline void update4(int x)
{
	while(q4.size()&&r2[q4.back()]>r2[x])q4.pop_back();
	q4.push_back(x);
}
inline bool check0(int x,int i)
{
	if(i-x<=0||i+x>n)return 0;
	int ll1=gan1(i-x,i)+x-i,rr1=gan2(i-x,i)-x+i;
	int ll2=max(gan3(i),l2[x+i])+x+i,rr2=min(gan4(i),r2[x+i])-x-i;
	if(max(ll1,ll2)<=min(rr1,rr2))return 1;
	return 0;
}
inline bool check1(int x,int i)
{
	if(i-(x+1)<=0||i+x+1>n)return 0;
	int ll1=gan1(i-(x+1),i)+(x+1)-i,rr1=gan2(i-(x+1),i)-(x+1)+i;
	int ll2=max(gan3(i),max(l2[x+i],l2[x+i+1]))+(x+1)+i,
	    rr2=min(gan4(i),min(r2[x+i],r2[x+i+1]))-(x+1)-i;
   if(max(ll1,ll2)<=min(rr1,rr2))return 1;
   return 0;	
}
signed main()
{
	int L,X,Y;ull A,B;cin>>n>>L>>X>>Y>>A>>B;
	gen(n,L,X,Y,A,B,l,r);int ans=0;
	bit[0]=1;for(int i=1;i<=n;i++)bit[i]=1ll*bit[i-1]*3%mod;
	for(int i=1;i<=n;i++)
	{
		l1[i]=l[i]+i;r1[i]=r[i]-i;
		l2[i]=l[i]-i;r2[i]=r[i]+i;
	}
	for(int i=1;i<=n;i++)
	{
		if(i==1)
		{
			q1.push_back(1);q2.push_back(1);
			q3.push_back(1);q4.push_back(1);
			f[i]=0;continue;
		}
		int x=f[i-1];
		if(check1(x,i))f[i]=x+1;
		else if(check0(x,i))f[i]=x;
		else f[i]=x-1;
		if(f[i]==x)update3(i+x),update4(i+x);
		else if(f[i]==x+1)update3(i+x),update3(i+x+1),update4(i+x),update4(i+x+1);
	}
	for(int i=1;i<=n;i++)ans=(ans+1ll*bit[i-1]*(f[i]+1)%mod)%mod;
	cout<<ans<<endl;
	return 0;
}

考试总结

1.想法多一点，想到就去实现
2.想不到正解也要想暴力，想更优的暴力，有分就是有分