dp泛做
模拟8 T3 超级树
这个主要是状态定义难想,如果想到了定义之后转移其实很好理解
状态是为了dp方便快速而设计的,好的状态定义可以简化状态转移,优化时间复杂度
设\(f_{i,j}\)表示在一棵\(i\)级超级树中,有\(j\)条路径同时存在且这\(j\)条路径没有公共点时总共的方案数
这个状态奇怪就奇怪在他新规定了一个没有公共点的路径这个东西,这个东西并不在题中让求的东西里,但他设计出了这个,为的是接下来可以转移做到不重不漏
然后考虑刷表,在从\(i\)级扩展到\(i+1\)级的时候,分别想新路径的构造方式然后转移就行
在取模很多并且时间比较紧的情况下,优化枚举范围也是一个重要技巧
详细题解见学长的博客,\(DC\)学长写的超详细,尤其是后面思维这一块很好,知其然知其所以然
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=305;
int f[N][4*N],n,mod;
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
signed main()
{
cin>>n>>mod;
f[1][0]=f[1][1]=1;
for(int i=1;i<=n;i++)
for(int j=0;j<=n-i+2;j++)
for(int k=0;k<=n-i+2-j;k++)
{
int sum=f[i][j]*f[i][k]%mod;
f[i+1][j+k]=add(f[i+1][j+k],sum);
f[i+1][j+k]=add(f[i+1][j+k],2*sum%mod*(j+k)%mod);
f[i+1][j+k+1]=add(f[i+1][j+k+1],sum);
f[i+1][j+k-1]=add(f[i+1][j+k-1],2*sum*j*k%mod);
f[i+1][j+k-1]=add(f[i+1][j+k-1],sum*(j*(j-1)+k*(k-1))%mod);
}
cout<<f[n][1]%mod<<endl;
return 0;
}
模拟28 T2 客星璀璨之夜
考虑贡献的来源与本质
由于问的是期望,而期望一定是由每段路径的贡献累积而成的,所以将他拆开,分别算每条路径的经过次数再乘贡献就行
设\(f_{i,j}\)表示当前还剩\(i\)个行星,第\(j\)段路径(\(x_j\)和\(x_{j+1}\),注意这里是星球)的期望经过次数
先计算剩\(i\)个星球选择的方案总数,就是\(g_i=2^n\times n!\)
考虑转移:
当前还有\(i\)个行星,考虑他选的是那一个星球,分三种情况:选了\(j\),\(j\)之前,\(j\)之后
选了\(j\)有贡献,就是\(g_{i-1}\),然后\(j\)这段的路径还会被\(f_{i-1,j-1}\)覆盖到,所以有贡献\(g_{i-1}+f_{i-1,j-1}\)
选了\(j\)前面的和后面的都没有贡献,只是有新路径覆盖的贡献,那么前面就是\(f_{i-1,j-2}\times (j-1)\)的贡献,后面就是\(f_{i-1,j}\times (2*i-j)\),累加起来就行
参考博客
网上题解大部分没有采用这种dp方式,有的进行了一次或两次预处理,还是要找到dp转移的本质
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod=998244353;
const int N=3030;
inline int ksm(int x,int y)
{
int s=1;x%=mod;
for(;y;y>>=1)
{
if(y&1)s=s*x%mod;
x=x*x%mod;
}
return s;
}
inline int ny(int x)
{
return ksm(x,mod-2);
}
int a[2*N],f[N][2*N],g[N],jc[N];
signed main()
{
int n;cin>>n;jc[0]=1;g[0]=1;
for(int i=1;i<=2*n+1;i++)scanf("%lld",&a[i]);
for(int i=1;i<=n;i++)jc[i]=jc[i-1]*i%mod;
for(int i=1;i<=n;i++)g[i]=ksm(2,i)*jc[i]%mod;
for(int i=1;i<=n;i++)
for(int j=1;j<=2*i;j++)
f[i][j]=(g[i-1]+f[i-1][j-1]+(j-1)*f[i-1][max((int)0,j-2)]%mod+(2*i-j)*f[i-1][j]%mod)%mod;
int ans=0;
for(int i=1;i<=2*n;i++)ans=(ans+f[n][i]*(a[i+1]-a[i])%mod)%mod;
cout<<ans*ny(g[n])%mod<<endl;
}
模拟20 T1玩具
首先转化题意,整个过程实际上就是有一颗树,1号节点固定,其他节点在\(1~i-1\)等概率随机一个父亲,求树的期望高度
题解似乎给出了一种考虑森林和树,类似背包的做法,不过需要处理3个dp数组,不太容易理解,可以换一种思路
明确一点这个题是假期望,等概率的期望dp都是计数题!
我们发现1,2号点是固定的,那么每个点要么在\(1\)的子树里要么在\(2\)的子树里,可以根据这个dp
设\(f_{i,j}\)表示树中有\(i\)个节点,树高为\(j\)的方案数,转移枚举1号节点和2号节点分别的子树大小和高度
其实有点树上合并的味道,只不过这个形态比较固定,方便理解可以刷表,就是
就是把两部分小的合成大的,加一是2子树的高还要加上它和1节点的连边,后面组合数是要选择点哪些属于1的子树,哪些属于2的,就是选择编号,1,2固定不能选要减去,其余比较显然
就像这个一样,要排编号
理解方程之后如果你直接开打的话可能会成这样
f[1][0]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=n-i;j++)
for(int k=0;k<i;k++)
for(int l=0;l<j;l++)
f[i+j][max(k,l+1)]=(f[i+j][max(k,l+1)]+f[i][k]*f[j][l]%mod*C(i+j-2,j-1)%mod)%mod;
然后你发现过不去样例,手模一下会发现,你的转移其实不能保证有序!
比如[4][2]有一种是由[1][0]和[3][1]转移过来,然而[3][1]由[2][0]和[1][0]转移过来,[3][1]还没有就被用到了
问题是当一个转态需要去更新别的状态时,他自己还没有被更新到,导致更新失败
所以我们换一种方式,枚举\(i+j\)和其中一颗子树的大小,这样就保证了转移正确性
f[1][0]=f[2][1]=1;
for(int i=3;i<=n;i++)
for(int j=1;j<=i-1;j++)
for(int k=0;k<j;k++)
for(int l=0;l<(i-j);l++)
f[i][max(k,l+1)]=(f[i][max(k,l+1)]+f[j][k]*f[i-j][l]%mod*C(i-2,j-1)%mod)%mod;
这个转移复杂度为\(n^4\),可以通过弱化版,,对于本题还要优化
应该砍一个\(n\),我们发现枚举比较多,所以看能不能前缀和优化
\(max\)不好处理,我们把它拆开,手动讨论两种情况
for(int l=0;l<min(i-j,k);l++)f[i][k]=(f[i][k]+f[j][k]*f[i-j][l]%mod*C(i-2,j-1)%mod)%mod;
for(int l=k;l<i-j;l++)f[i][l+1]=(f[i][l+1]+f[j][k]*f[i-j][l]%mod*C(i-2,j-1)%mod)%mod;
上面的已经可以直接前缀和了,下面的由于\(k,l\)优先级相同,可以改变顺序,就也可以前缀和了
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,mod;
inline int ksm(int x,int y)
{
int s=1;x%=mod;
for(;y;y>>=1)
{
if(y&1)s=s*x%mod;
x=x*x%mod;
}
return s;
}
const int N=350;
int f[N][N],jc[2*N],ny[2*N],jcny[2*N],inv[N];
inline int C(int x,int y)
{
if(x<y)return 0;
if(!y)return 1;
return jc[x]*jcny[y]%mod*jcny[x-y]%mod;
}
signed main()
{
cin>>n>>mod;
inv[1]=1;jc[0]=1;jc[1]=1;jcny[0]=1;jcny[1]=1;
for(int i=2;i<=350;i++)
{
jc[i]=jc[i-1]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
jcny[i]=jcny[i-1]*inv[i]%mod;
}
f[1][0]=f[2][1]=1;int ans=0;
for(int i=3;i<=n;i++)
for(int j=1;j<i;j++)
{
int c=C(i-2,j-1),sum=0;
for(int k=0;k<j;k++)
{
f[i][k]=(f[i][k]+f[j][k]*sum%mod*c%mod)%mod;
sum=(sum+f[i-j][k])%mod;
}
sum=0;
for(int l=0;l<i-j;l++)
{
if(l<=j)sum=(sum+f[j][l])%mod;
f[i][l+1]=(f[i][l+1]+sum*f[i-j][l]%mod*c%mod)%mod;
}
}
for(int i=1;i<n;i++)ans=(ans+f[n][i]*i%mod)%mod;
cout<<ans*jcny[n-1]%mod<<endl;
return 0;
}
这个题在于把握住全局和局部的关系,通过改变枚举对象来达到有序转移
模拟47 T2.Sequence
dp关键在于设计状态,这个题也不例外
表面上看上去是个计数,其实他的突破口在数据范围上
\(m\)到了\(1e18\),这种东西显然不能作为dp数组大小的,想要解决这个一般需要矩阵快速幂,与之配套的是一个较小的数据范围,\(k<=100\),有了,这种情况下转移方程一般不会很复杂,所以我们看有没有和\(k\)相关的状态可以设计
dp设计状态要紧盯着数据范围,尤其是数据范围差别比较大的时候
设\(f_i\)表示以\(i\)结尾的子序列个数,那么对于下一个元素\(x\)有
其他元素都不改变,应该比较好理解,往后放一个\(x\),那么原来所有以任何数结尾的都可以新增一个\(x\)贡献到\(f_x\)上,原来为空的也可以加上一个单独的\(x\)变成合法,所以要加一
这个东西能想出来关键在提取有用信息,这种序列统计一般不会关注整个序列是啥,大多关注开头,结尾,长度等信息
dp设计状态另一个重要思想是忽略,把看似很难求的东西转化,提取一部分东西作为状态简化问题
维护一个\(sum\)就能求出原有的答案,考虑往后填什么,因为不管后面的\(x\)是啥新的\(f_x\)都是一定的,肯定往后填原来dp值最小的,注意这里不能排序,因为有取模,应该按照上一次出现位置排序
新填的一定循环,考虑矩阵优化,配一个矩阵,每次让一个元素加上所有元素之和,然后把要拿得换到前面
由于要加一,所以矩阵是\((n+1)\times (n+1)\)的,因为一个数被更新之后就放到了最后,所以可以直接处理要填的顺序,我们希望乘出来之后能把最前面的放到最后,其余都往前移且dp值不变,就有这么一个东西
\(\begin{bmatrix}0&0&0&0&1&0\\1&0&0&0&1&0\\0&1&0&0&1&0\\0&0&1&0&1&0\\0&0&0&1&1&0\\0&0&0&0&1&1\end{bmatrix}\)
对角线向下平移,再加一列,最后来个1
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod=1e9+7;
const int N=1000050;
int last[105],a[N],n,m,k;
int p[105],s[105][105],f[105];
inline bool cmp(int x,int y)
{
return last[x]<last[y];
}
int pp[105][105],an[105];
inline void gan()
{
memset(pp,0,sizeof(pp));
for(int i=1;i<=k+1;i++)
for(int j=1;j<=k+1;j++)
for(int kk=1;kk<=k+1;kk++)
pp[i][j]=(pp[i][j]+s[i][kk]*s[kk][j]%mod)%mod;
memcpy(s,pp,sizeof(pp));
}
inline void mul()
{
memset(an,0,sizeof(an));
for(int i=1;i<=k+1;i++)
for(int j=1;j<=k+1;j++)
an[i]=(an[i]+f[j]*s[j][i]%mod)%mod;
memcpy(f,an,sizeof(f));
}
inline void ksm(int x)
{
for(;x;x>>=1)
{
if(x&1)mul();
gan();
}
}
signed main()
{
cin>>n>>m>>k;
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
int sum=0,ans=0;
for(int i=1;i<=n;i++)
{
int x=a[i],pp=f[x];
last[x]=i;
f[x]=(sum+1)%mod;
sum=(sum+f[x]-pp+mod)%mod;
}
for(int i=1;i<=k;i++)p[i]=i;
sort(p+1,p+k+1,cmp);
memcpy(an,f,sizeof(an));
for(int i=1;i<=k;i++)f[i]=an[p[i]];
for(int i=1;i<=k+1;i++)
{
s[i][k]=1;
if(i>1)s[i][i-1]=1;
}
f[k+1]=1;s[k+1][k+1]=1;
ksm(m);
for(int i=1;i<=k;i++)ans=(ans+f[i])%mod;
cout<<ans<<endl;
return 0;
}
模拟29 T2.完全背包问题
背包看似比较基础,不过他能玩出好多奇怪的东西
给一些物品问是否能把背包装满,对大体积物品选取的数量有限制
多组询问显然不能对每个\(w\)分别做,应该一遍dp之后直接\(check\),显然背包dp复杂度与值域有关
如果没有大体积限制就是背包九讲的板子了,加上限制之后怎么办?限制多了,加维
发现物品数比较少,限制个数也不多,一个比较简单的dp是在\(w\)较小的时候,设\(f_{i,j,k}\)表示选了前\(i\)个物品,大体积物品数量不超过\(j\),是否存在总体积为\(k\)的方案,布尔数组,按着套路转移就行,分当前的物品是否受限
现在问题来了,值域足足有\(10^18\),直接做肯定不行,思考怎么解决
值域极大时一种方法是给他带上\(log\),例如矩阵快速幂和数位dp,但显然这里都不适用,其实我们还有一种方法:同余
试图找到一种循环之类的规律,能只考虑\(w\)对一个相对较小的数取模的值,分析一下会发现这个跟\(L\)大小有关系
设所有\(v\)之中最小的是\(v_0\),如果\(v_0>=L\),那么他一定受限,最大背包体积不超过\(cV\),于是就是上面的第一个转移,用bitset优化一下可以保证正确的时空复杂度,同时也可以用两个bitset直接或上来代替\(k\)的枚举
其实题里面根本没有这样的数据
如果\(v_0<L\),那么对于一个合法的\(w\),一定可以多\(v_0\)凑出一个新的,答案存在单调性,于是我们更换状态定义
设\(f_{i,j,k}\)表示考虑到\(i\)个,大体积个数为\(j\),所有可行的体积方案中对\(j\)取模最小的值
这个看上去似乎不好理解,实际上这就让它的值域缩小了,考虑一个\(w\),如果在大体积个数确定的情况下,\(w>=f_{n,j,w\mod v_0}\)则合法,由于这里不在是布尔数组,所状态定义稍微变一下,变成钦定\(j\),每次取\(min\)
发现第二个柿子转移无序,应对策略是对dp状态建图跑最短路,建一个有\(v_0+1\)个点的有向图,从源点\(s\)向每个\(k\)连边权为\(f_{i-1,j,k}\)的边,每个\(k\)向\((k+v_i)\mod v_0\)连边权为\(v_i\)的边,spfa或dij
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=10500;
int v[N],n,m,l,c;
bitset <30*N> f[35][55];
inline void gan1()
{
f[0][0][0]=1;
for(int i=1;i<=n;i++)for(int j=0;j<=c;j++)
{
f[i][j]=f[i-1][j];
if(j)f[i][j]|=(f[i][j-1]<<v[i]);
}
for(int i=1;i<=m;i++)
{
int x;scanf("%lld",&x);
if(x>c*v[n]){puts("No");continue;}
if(f[n][c][x])puts("Yes");
else puts("No");
}
}
int g[55][35][N];
struct node{
int from,to,next,w;
}a[2*N];
int head[N],mm=1;
inline void add(int x,int y,int w)
{
a[mm].from=x;a[mm].to=y;a[mm].w=w;
a[mm].next=head[x];head[x]=mm++;
}
int mp[N],tot,s,d[N];
inline void build(int i,int j)
{
memset(a,0,sizeof(a));mm=1;
memset(head,0,sizeof(head));
for(int k=0;k<v[1];k++)add(s,mp[k],g[i-1][j][k]);
for(int k=0;k<v[1];k++)add(mp[k],mp[(k+v[i])%v[1]],v[i]);
}
queue <int> q;bool vis[N];
inline void spfa(int i,int j)
{
build(i,j);memset(d,0x3f,sizeof(d));
d[s]=0,vis[s]=1;q.push(s);
while(q.size())
{
int x=q.front();q.pop();vis[x]=0;
for(int ii=head[x];ii;ii=a[ii].next)
{
int y=a[ii].to;
if(d[y]>d[x]+a[ii].w)
{
d[y]=d[x]+a[ii].w;
if(!vis[y])q.push(y),vis[y]=1;
}
}
}
for(int k=0;k<v[1];k++)g[i][j][k]=d[mp[k]];
}
int mi[N];
inline void gan2()
{
memset(g,0x3f,sizeof(g));g[0][0][0]=0;
s=++tot;for(int i=0;i<v[1];i++)mp[i]=++tot;
for(int i=1;i<=n;i++)
{
if(v[i]>=l)
{
for(int j=0;j<=c;j++)
for(int k=0;k<v[1];k++)
g[i][j][k]=min(g[i-1][j][k],(j>0?g[i][j-1][((k-v[i])%v[1]+v[1])%v[1]]:(int)1e17)+v[i]);
}
else for(int j=0;j<=c;j++)spfa(i,j);
}
for(int i=1;i<=m;i++)
{
int x;scanf("%lld",&x);bool flag=0;
for(int j=0;j<=c;j++)if(x>=g[n][j][x%v[1]]){puts("Yes"),flag=1;break;}
if(!flag)puts("No");
}
}
signed main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)scanf("%lld",&v[i]);
sort(v+1,v+n+1);cin>>l>>c;
if(v[1]>=l)gan1();
else gan2();
return 0;
}
这个告诉我们带模的状态定义和建图dp转移两个技巧
一般来说对于无序转移,加减法考虑高斯消元,最值考虑建图
模拟53 T4.计数
学长出的dp好题,结合了树的一些性质
首先满足前序遍历就有如下性质

考虑中序遍历,对于一个限制强制\(a<b\),那么\(a,b\)的限制关系有两种:\(a\)在\(b\)前或后

最终我们还是要dp的,那么限制就可以转化成对于\(a\)的左子树大小的限制:
若满足限制1,那么b必然在a的子树里,所以\(a\)的左子树一定要放的下\(b\),即不小于\(b-a\)
若满足限制2,那么b必然不在,于是\(a\)的左子树大小要小于\(b-a\)
所以只要处理出上下界就可以了,转移按照套路枚举左子树大小,设\(f_{i,j}\)表示以\(i\)为根大小为\(j\)的方案数,就有
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=405,M=1005;
const int mod=1e9+7;
int f[N][N],p1[N],p2[N];
inline void clear()
{
memset(f,0,sizeof(f));
memset(p1,0,sizeof(p1));
memset(p2,0,sizeof(p2));
}
signed main()
{
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
int t;cin>>t;
while(t--)
{
clear();
int n,m;scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)p1[i]=0,p2[i]=n-i+1;
for(int i=1;i<=m;i++)
{
int x,y;scanf("%lld%lld",&x,&y);
bool flag=0;if(x>y)swap(x,y),flag=1;
if(flag)p1[x]=max(p1[x],y-x);
else p2[x]=min(p2[x],y-x);
}
f[n][1]=1;
for(int i=n-1;i>=1;i--)
for(int k=p1[i];k<p2[i];k++)
for(int j=k+1;j<=n-i+1;j++)
f[i][j]=(f[i][j]+(k?f[i+1][k]:1)*(j-1-k?f[i+1+k][j-1-k]:1)%mod)%mod;
printf("%lld\n",f[1][n]);
}
return 0;
}
并不难,主要是思维上有特点
模拟60 T3 打字机
这个题感觉思维很好,但是没有题解啥也不会
暴力就是设计一个状态\(f_{i,j}\),表示两个串分别匹配了多少的答案,转移就是
就是一个魔改的公共子序列,考场写挂了
然后想正解,发现dp瓶颈在对于每个询问都做了一次,所以思考下能不能直接一次出答案,然后通过简单处理解决每个询问
由于子串都是前缀后缀,这里一个好的方法是对于每个前缀处理后缀信息
然后就神仙了:设对于\(S\)长度为\(i\)的后缀答案是\(h(i)\),他定义了一个\(F\)函数\(F(x)=x-h(x)\),然后对着\(F\)搞
为啥呢?因为这个\(F\)有很好的性质
首先它的值单调,因为\(i\)每增加1的时候,\(h(i)\)最多增加1,所以说单调
其次它的值域很小,任意\(x\)有\(-|T|<=F(x)<=|T|\),这个也不难理解
当直接不容易dp的时候,可以把相关的量设计成状态,通过一些性质设计方程
由于它的值域单调,所以我们可以设计更为高效的dp,用分段函数实现转移
设\(f_{i,j,k}\)表示匹配到\(S\)的\(i\)位,到\(T\)的\(j\)位,此时后缀为\(k\)的\(F(k)\)值,然后和暴力类似的转移
然而会发现复杂度依然不对,现在你可以\(O(1)\)回答,但转移复杂度还是\(O(|S|^2|T|)\),也不太行
考虑第二个性质,这个20很好,所以考虑将下标和值域互换
重来,\(f_{i,j,k}\)成为使得\(F(x)<=k\)的最大\(x\),然后所有都会反过来,注意这里下标可能为负要处理一下
初始化考虑实际意义,似乎有点复杂,下面\(dp2\)即为\(f\)
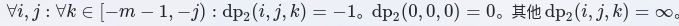
那个-1是不合法特判,方便转移,方程如下,刷表很方便
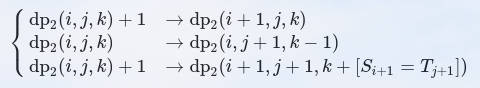
然后就有代码了
#include <bits/stdc++.h>
using namespace std;
const int N=100020;
int f[N][22][42];
char s[N],t[24];
inline int h1(int x){return x+21;}
signed main()
{
freopen("print.in","r",stdin);
freopen("print.out","w",stdout);
scanf("%s%s",s+1,t+1);
memset(f,0x3f,sizeof(f));
int l1=strlen(s+1),l2=strlen(t+1);
for(int i=0;i<=l1;i++)for(int j=0;j<=l2;j++)
for(int k=-l2-1;k<=-j-1;k++)f[i][j][h1(k)]=-1;
f[0][0][h1(0)]=0;
for(int i=0;i<=l1;i++)for(int j=0;j<=l2;j++)
for(int k=-l2-1;k<=l2;k++)
{
f[i+1][j][h1(k)]=min(f[i+1][j][h1(k)],f[i][j][h1(k)]+1);
if(k>=-l2)f[i][j+1][h1(k-1)]=min(f[i][j+1][h1(k-1)],f[i][j][h1(k)]);
f[i+1][j+1][h1(k+(s[i+1]==t[j+1]))]=min(f[i+1][j+1][h1(k+(s[i+1]==t[j+1]))],f[i][j][h1(k)]+1);
}
int m;cin>>m;
for(int i=1;i<=m;i++)
{
int l,r;scanf("%d%d",&l,&r);
int len=r-l+1,an;
for(int j=-l2;j<=l2;j++)
if(f[r][l2][h1(j)]>=len)
{an=j;break;}
printf("%d\n",len-an);
}
return 0;
}
技巧很有用,但是这样dp细节一般不会少


 浙公网安备 33010602011771号
浙公网安备 33010602011771号