模拟44 考试总结
如果深渊呼唤我 我就走向深渊
考试经过
感觉精神不错,上来看T1,想到可以搞转化区间覆盖再判合不合法,感觉可以线段树,发现值域很大,开始想动态开点结果发现空间不够,接着冥思苦想离散化细节
1h无果先看看后面的题,靠都啥玩意啊!!!
认为后面极不可做所以死磕T1,三个小时的时候调完了,看了两眼就交了
然后准备冲暴力,T2看着像数位dp但是不会,打了个最暴力的暴力,T4没看懂题弃了,T3打了几个表但是找不到规律,想着再有一两个小时问题应该不大,然而不会暴力,瞄准1分冲了一发
期望:100+20+1+0=121
实际:0+0+5+0=5
淦。。。
没有逃脱线段树必假魔咒啊
一看人傻了,快读挂了

我就是智障
后来发现改了还是爆零,整半天少判了不合法状态。。。
啥时候能想明白了再打啊……
T1 Emotional Flutter
把所有黑段两个端点分别对\(k\)取模,然后转化为\(1-k\)的区间覆盖,最后看剩下连续区间长是不是大于等于\(s\)就行
具体分成两种情况,模完之后如果\(l\)小于等于\(r\)就从\(l\)到\(r\)覆盖,否则覆盖\(1\)到\(r\)和\(l\)到\(k\)
权值太大要离散化,可以将整个区间分成一些点和段,有端点覆盖的就是权值为1点,一段没有 覆盖端点 的区间可以缩成一个权值为区间长度的点,其实点全职就是区间长
注意如果发现一段黑的超过了\(k-s\)直接无解
然后线段树就被时空双爆了
#include <bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
int x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const int N=500050;
struct tree{
int ls,rs,sum;bool lazy;
}tr[6*N];
int a[N],b[N],w[2*N],lsh[2*N],mp[N],d[N],num;
inline void qi(int id,int l,int r)
{
tr[id].ls=tr[id*2].ls;int mid=(l+r)>>1;
if(tr[id*2].ls==lsh[mid]-lsh[l-1])tr[id].ls+=tr[id*2+1].ls;
tr[id].rs=tr[id*2+1].rs;
if(tr[id*2+1].rs==lsh[r]-lsh[mid+1-1])tr[id].rs+=tr[id*2].rs;
tr[id].sum=max(max(tr[id*2].sum,tr[id*2+1].sum),tr[id*2].rs+tr[id*2+1].ls);
}
inline void luo(int id,int l,int r)
{
if(l!=r&&tr[id].lazy)
{
tr[id*2].ls=tr[id*2].rs=tr[id*2].sum=0;
tr[id*2+1].ls=tr[id*2+1].rs=tr[id*2+1].sum=0;
tr[id*2].lazy=tr[id*2+1].lazy=1;
tr[id].lazy=0;
}
}
void build(int id,int l,int r)
{
tr[id].lazy=0;
if(l==r)
{
tr[id].rs=tr[id].ls=tr[id].sum=w[l];
return;
}
int mid=(l+r)>>1;
build(id*2,l,mid);build(id*2+1,mid+1,r);
qi(id,l,r);
}
void add(int id,int ll,int rr,int l,int r)
{
if(l>r)return;
if(l<=ll&&r>=rr)
{
tr[id].ls=tr[id].rs=tr[id].sum=0;
tr[id].lazy=1;return;
}
luo(id,ll,rr);int mid=(ll+rr)>>1;
if(r<=mid) add(id*2,ll,mid,l,r);
else if(l>mid) add(id*2+1,mid+1,rr,l,r);
else add(id*2,ll,mid,l,mid),add(id*2+1,mid+1,rr,mid+1,r);
qi(id,ll,rr);
}
inline int gen(int x)
{
if(x&1)return (x+1)>>1;
return x>>1;
}
signed main()
{
int t=read();
while(t--)
{
int s=read(),k=read(),n=read();num=0;
for(int i=1;i<=n;i++)a[i]=read();
int p=gen(n)<<1,ss=0;bool die=0;
for(int i=1;i<=n;i++)
{
ss+=a[i];if(!(i&1))continue;
if(a[i]>k){puts("NIE");die=1;break;}
int lp=(ss-a[i]+1)%k,rp=ss%k;
if(lp==0)lp=k;if(rp==0)rp=k;
b[i]=lp,b[i+1]=rp;
}
if(die)continue;
for(int i=1;i<=p;i++)lsh[i]=b[i];
sort(lsh+1,lsh+p+1);
int cnt=unique(lsh+1,lsh+p+1)-lsh-1;
for(int i=1;i<=p;i++)
{
int ga=b[i];
b[i]=lower_bound(lsh+1,lsh+cnt+1,ga)-lsh;
mp[b[i]]=ga;
}
for(int i=1;i<=cnt;i++)
{
if(mp[i]-mp[i-1]>1)w[++num]=mp[i]-1-mp[i-1];
w[++num]=1;d[i]=num;
}
if(mp[cnt]<k)w[++num]=k-mp[cnt];
memset(lsh,0,sizeof(lsh));
for(int i=1;i<=num;i++)lsh[i]=lsh[i-1]+w[i];
build(1,1,num);
for(int i=1;i<=p;i+=2)
{
int ll=d[b[i]],rr=d[b[i+1]];
if(ll<=rr)add(1,1,num,ll,rr);
else add(1,1,num,ll,num),add(1,1,num,1,rr);
}
if(tr[1].sum<s)puts("NIE");
else puts("TAK");
}
return 0;
}
注意这里的\(lsh\)数组进行了反复利用,后一次是作为\(w\)的前缀和用的
其实根本不用线段树,一个差分就完事了
AC代码
#include <bits/stdc++.h>
using namespace std;
#define gc if(++ip==ie)fread(ip=buf,1,SZ,stdin)
const int SZ=1<<19;
char buf[SZ],*ie=buf+SZ,*ip=ie-1;
inline int read(){
gc;while(*ip<'-')gc;
bool f=*ip=='-';if(f)gc;
int x=*ip&15;gc;
while(*ip>'-'){x*=10;x+=*ip&15;gc;}
return f?-x:x;
}
const int N=500050;
int a[N],b[N],w[2*N],lsh[2*N],mp[N],d[N],num;
int f[2*N],ff[2*N],pp[2*N];
inline int gen(int x)
{
if(x&1)return (x+1)>>1;
return x>>1;
}
signed main()
{
int t=read();
while(t--)
{
num=0;int s=read(),k=read(),n=read();
memset(f,0,sizeof(f));
for(register int i=1;i<=n;i++)a[i]=read();
int p=gen(n)<<1;long long ss=0;bool die=0;
for(register int i=1;i<=n;i++)
{
ss+=a[i];if(!(i&1))continue;
if(a[i]>k-s){puts("NIE");die=1;break;}
int lp=(ss-a[i]+1)%k,rp=ss%k;
if(lp==0)lp=k;if(rp==0)rp=k;
b[i]=lsh[i]=lp,b[i+1]=lsh[i+1]=rp;
}
if(die)continue;
sort(lsh+1,lsh+p+1);
int cnt=unique(lsh+1,lsh+p+1)-lsh-1;
for(register int i=1;i<=p;i++)
{
int ga=b[i];
b[i]=lower_bound(lsh+1,lsh+cnt+1,ga)-lsh;
mp[b[i]]=ga;
}
memset(lsh,0,sizeof(lsh));
for(register int i=1;i<=cnt;i++)
{
if(mp[i]-mp[i-1]>1)w[++num]=mp[i]-1-mp[i-1],lsh[num]=lsh[num-1]+w[num];
w[++num]=1,lsh[num]=lsh[num-1]+w[num];d[i]=num;
}
if(mp[cnt]<k)w[++num]=k-mp[cnt],lsh[num]=lsh[num-1]+w[num];
for(int i=1;i<=p;i+=2)
{
int ll=d[b[i]],rr=d[b[i+1]];
if(ll<=rr)f[ll]++,f[rr+1]--;
else f[ll]++,f[num+1]--,f[1]++,f[rr+1]--;
}
int ans=0;
for(int i=1;i<=num;i++)
{
ff[i]=ff[i-1]+f[i];
if(ff[i]>0)pp[i]=0;
else pp[i]=pp[i-1]+w[i];
ans=max(ans,pp[i]);
}
if(ans<s)puts("NIE");
else puts("TAK");
}
return 0;
}
由于是在卡常代码的基础上改的所以比较丑
T2. Medium Counting
神仙dp,根本不会,然而还是要复读一下题解
设\(f_{l,r,x,lim}\)表示当前处理了从\(l\)到\(r\)的字符串,考虑它们从\(x\)开始的后缀,保证字典序,且要求第\(p\)位的字母至少是\(lim\)的方案数
说白了就是干这么一个事:
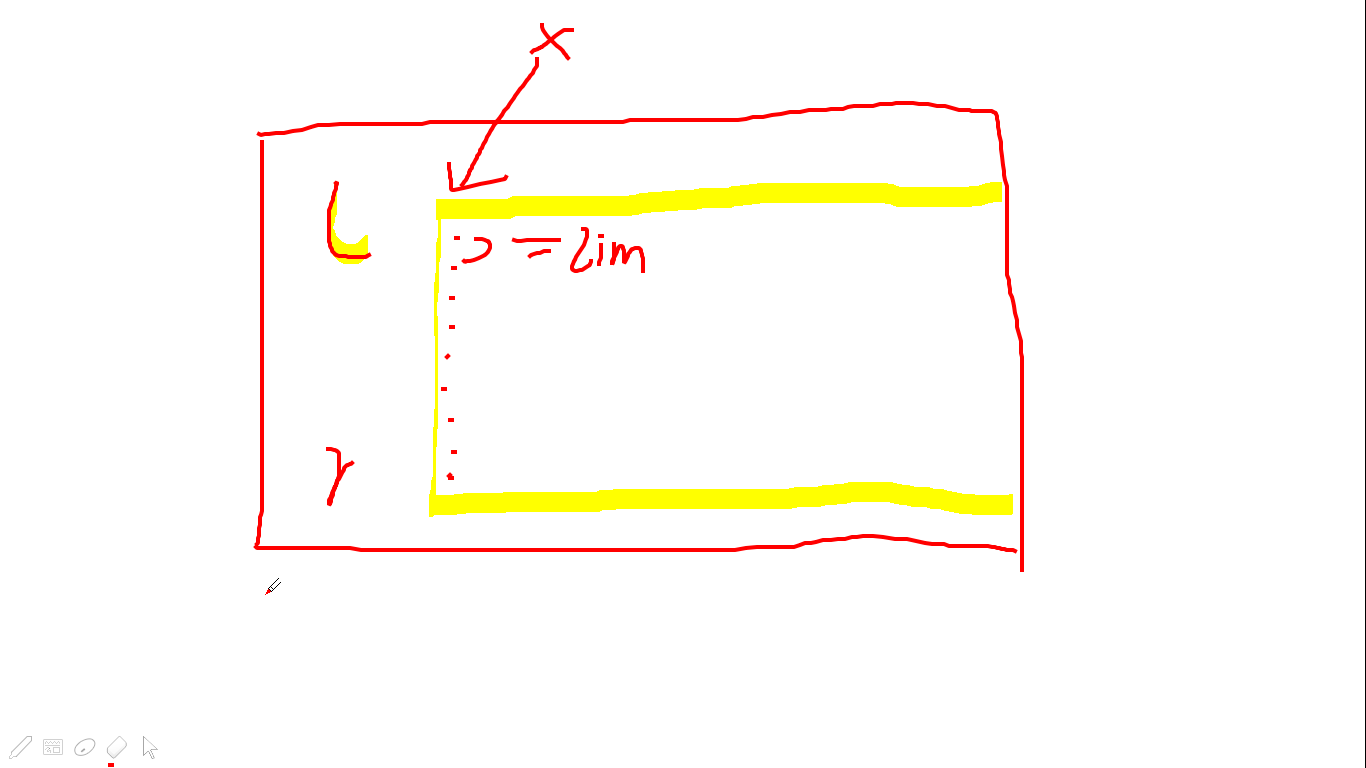
黄色部分就是考虑的区域
考虑两种转移:
第一个就是考虑填更大的\(lim\),即直接转移到\(f_{l,r,x,lim+1}\)
第二个就有点复杂,也是这个题思路的巧妙所在
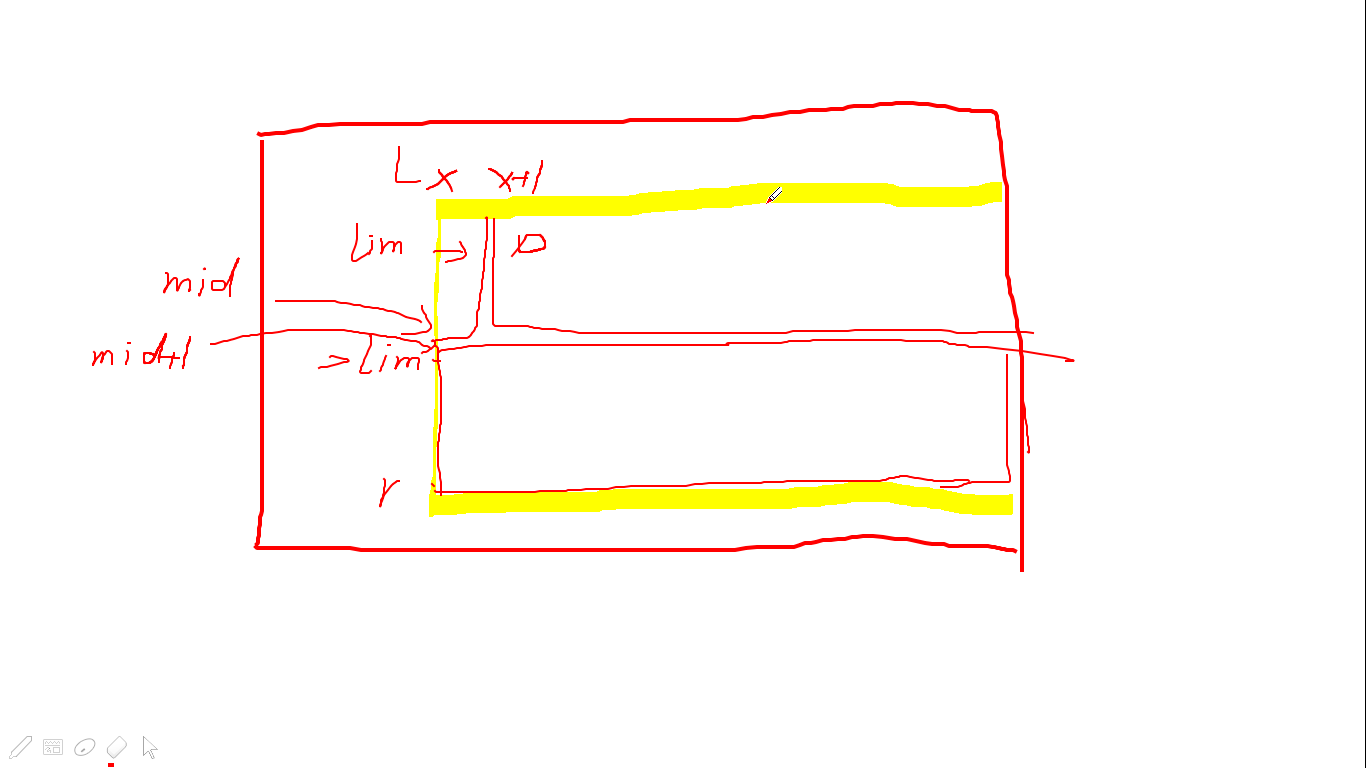
枚举一个在\(l\)和\(r\)之间的\(mid\),强制让它之上的一列都填成\(lim\),然后就可以划分子问题,转移用\(f_{l,mid,x+1,0}\times f_{mid+1,r,x,lim+1}\)贡献答案
反正我想不到,毕竟战神是战神
思考一下正确性是有的,接下来就是恶心的实现了
懒人适用dfs记捜,着重说一下边界和判定
如果\(lim\)大于26了返回0,如果\(l\)大于\(r\)返回1,\(x\)如果大于\(m\)返回\(l==r\)一个0或1,具体要看实际意义,chy说看这种情况是怎么出来的,加出来的就是0,乘出来的就是1,貌似有些道理
这里\(mid\)要枚举到\(r\),不合法返回\(1\),原因是要累加乘号前面的答案
关于跳出条件,发现如果想要把上面的全填成\(lim\),必须要保证合法,就是上面的必须都是只有问好和\(lim\)这个字母,感性理解下这个条件其实很苛刻,转移不会很多
还有就是如果字符串不等长要在后面补0,就是\(a-1\)这个字母,如果\(lim\)是0但这一位是问号,也是不合法的,因为这时只有不填合法,空字符串字典序最小
然后终于能放代码了
#include <bits/stdc++.h>
using namespace std;
const int mod=990804011;
#define int long long
char a[55][25];
int n,m;int mem[55][55][25][30];
int dfs(int l,int r,int x,int lim)
{
if(mem[l][r][x][lim]!=-1)return mem[l][r][x][lim];
if(l>r)return mem[l][r][x][lim]=1;
if(x>m)return mem[l][r][x][lim]=(l==r);
if(lim>26)return mem[l][r][x][lim]=0;
int ans=0;
ans=(ans+dfs(l,r,x,lim+1))%mod;
for(int i=l;i<=r;i++)
{
if(a[i][x]!='?'&&a[i][x]!=lim+'a'-1)break;
if(a[i][x]=='?'&&lim==0)break;
ans=(ans+dfs(l,i,x+1,0)*dfs(i+1,r,x,lim+1)%mod)%mod;
}
mem[l][r][x][lim]=ans;
return ans;
}
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%s",a[i]+1);
m=max(m,(int)strlen(a[i]+1));
}
for(int i=1;i<=n;i++)
{
int p=strlen(a[i]+1);
for(int j=p+1;j<=m;j++)
a[i][j]='a'-1;
}
memset(mem,-1,sizeof(mem));
cout<<dfs(1,n,1,0)<<endl;
return 0;
}
数位dp题做的不多,要积累技巧
T3.Huge Counting
数学题,可以发现每个点\(f\)函数的值就是多重集排列,详见此
然后考虑计算答案,对于每个点答案可以在\(log\)时间计算出来,就是
其实就是算2因子的个数,考虑什么时候有贡献,只有在这个柿子答案是0的时候才有贡献,因为这样模2才有余数
进一步撕烤,无数奇怪脑洞之后发现答案和\(\sum x_i\)有关,所有\(x_i\)在二进制下加起来每一位最多有一个1,否则产生进位会造成向下取整后原柿子一定大于零
解释一下,比如一个点在每一维上的坐标分别是\(1001\),\(0100\),\(0010\)就是合法的,\(f\)最后是1,如果出现\(1001\)和\(1100\)就不合法,函数值是0
问题转化成了求在每一维找一个点,最终各个点的二进制位不重叠的方案数,并且每一维点的区间都有限制
所以就又是数位dp了,分别记录当前位数的和每一维是否受限,转移考虑那个1在拿一维被选或不选1,比前一个题要简单
对于左边界只要容斥就行了,复杂度\(O(2^{2k}n)\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int mod=990804011;
int l[11],r[11];int n;
int mem[62][1<<10],p[12];
int dfs(int x,int lim)
{
if(mem[x][lim]!=-1)return mem[x][lim];
if(!x)return mem[x][lim]=1;
int ans=0,s=0;
for(int i=1;i<=n;i++)
{
if((p[i]>>(x-1))&1)continue;
if((lim>>(i-1))&1)s|=(1<<(i-1));
}
ans=(ans+dfs(x-1,s))%mod;
for(int i=1;i<=n;i++)
{
if((lim>>(i-1))&1){if((p[i]>>(x-1))&1)ans=(ans+dfs(x-1,s|(1<<(i-1))))%mod;}
else ans=(ans+dfs(x-1,s))%mod;
}
mem[x][lim]=ans;
return ans;
}
signed main()
{
int t;cin>>t;
while(t--)
{
scanf("%lld",&n);
memset(mem,-1,sizeof(mem));
for(int i=1;i<=n;i++)scanf("%lld%lld",&l[i],&r[i]);
for(int i=1;i<=n;i++)l[i]--,r[i]--;
int ans=0,flag=(n&1)^1;
for(int i=0;i<=(1<<n)-1;i++)
{
int sum=0;bool die=0;
memset(mem,-1,sizeof(mem));
for(int j=1;j<=n;j++)
{
if((i>>(j-1))&1)p[j]=r[j],sum++;
else p[j]=l[j]-1;
if(p[j]<0){die=1;break;}
}
if(die)continue;
if((sum&1)^flag)ans=(ans+dfs(60,(1<<n)-1))%mod;
else ans=(ans-dfs(60,(1<<n)-1)+mod)%mod;
}
printf("%lld\n",ans);
}
return 0;
}
这题难度主要在转化题意和思维上,不要被花里胡哨的题目吓倒
T4
结论题但没人会证,所以咕了
考试总结
1.不要想到啥就开打,好歹整理一下思路,把情况一定要考虑清楚
2.自己把握时间,不要高估自己打暴力的效率和准确性


 浙公网安备 33010602011771号
浙公网安备 33010602011771号