模拟34 考试总结

考试经过
别自欺欺人了,你菜的一批

好吧又挂没了
T1想到二分然后快速打出两个\(log\)做法,结果因为乱卡常把边界搞炸了挂掉\(34pts\)
T2也是正解,因为线段树被卡常,结果一车\(86\)的
T3乱搞了一个状压滚粗了,本来能\(rk4\)的,结果……
也许只有简单题才能想到正解吧,然而有了正解也有拿不了的分啊……
还是自己太弱了啊
T1.Merchant
先证明单调性:由于每个都是一次函数,所以和起来一定是一次函数:当斜率为负就是0,否则就单调升可以二分,然后就莽就行了
有一个叫做\(nth-element\)的函数,利用快排只递归一半可以\(O(n)\)求出序列第\(k\)大数,具体就是传入首尾迭代器和\(k\),用法如下:
nth_element(a+1,a+k+1,a+n+1);
记得\(k\)放在中间,它会把你要的数放在第\(k\)位上,这样就能\(O(n) check\)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ld long double
#define R register
const int N=1000500;
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x*f;
}
int a[N],b[N],n,m,s;
ld q[N];int tot;
inline bool check(int x)
{
ld ans=0;
memset(q,0,sizeof(q));tot=0;
for(R int i=1;i<=n;i++)
{
ld an=a[i]*x+b[i];
if(an<=0)continue;
q[++tot]=an;
}
int ga=tot-min(tot,m)+1;
nth_element(q+1,q+ga+1,q+tot+1);
int p=q[ga],num=0;
for(R int i=1;i<=tot;i++)if(q[i]>=p)ans+=q[i],num++;
if(num>m)ans=ans-(ld)(num-m)*p;
if(ans-s>=0)return 1;
else return 0;
}
inline int er(int l,int r)
{
if(l>=r)return r;
int mid=(l+r)>>1;
if(check(mid))return er(l,mid);
else return er(mid+1,r);
}
signed main()
{
cin>>n>>m>>s;
bool flag=1;
for(int i=1;i<=n;i++)a[i]=read(),b[i]=read();
if(check(0))
{puts("0");return 0;}
cout<<er(1,1e9);
return 0;
}
可能会爆\(long long\),可以用\(long double\)
T2.Equation
会发现直接高斯消元挂成和爆搜一个分,所以考虑正解
由于他只要求\(x_1\),所以我们利用各个式子都可以得到形如\(x_1\pm x_i=w\)的形式,具体就是在树上dfs一遍,根据深度的奇偶判断应该加还是减当前边权,然后对于询问直接手动讨论情况解方程,修改就是个区间修改,有\(dfs\)序都好说
正解好像是树状数组,不过我利用不建树的线段树成功卡过,而且跑的比大部分树状数组都快
#include <bits/stdc++.h>
using namespace std;
const int N=1000050;
#define R register
#define gc if(++ip==ie)fread(ip=buf,1,SZ,stdin)
const int SZ=1<<19;
char buf[SZ],*ie=buf+SZ,*ip=ie-1;
inline long long read(){
gc;while(*ip<'-')gc;
bool f=*ip=='-';if(f)gc;
int x=*ip&15;gc;
while(*ip>'-'){x*=10;x+=*ip&15;gc;}
return f?-x:x;
}
struct node{
int from,to,next,w;
}a[2*N];
int head[N],mm=1;
inline void add(int x,int y,int w)
{
a[mm].from=x;a[mm].to=y;a[mm].w=w;
a[mm].next=head[x];head[x]=mm++;
}
int d[N],fa[N],size[N];
int id[N],rk[N],tot,w[N],ww[N];
void dfs(int x)
{
id[x]=++tot;rk[tot]=x;
for(int i=head[x];i;i=a[i].next)
{
int y=a[i].to;
d[y]=d[x]+1;fa[y]=x;
if(d[x]&1)w[y]=w[x]+a[i].w;
else w[y]=w[x]-a[i].w;
dfs(y);
size[x]+=size[y];
}
size[x]++;
}
struct tree{
int lazy;
}tr[4*N];
inline void luo(int id,int l,int r)
{
if(l!=r&&tr[id].lazy)
{
tr[id<<1].lazy+=tr[id].lazy;
tr[id<<1|1].lazy+=tr[id].lazy;
tr[id].lazy=0;
}
}
inline void change(int id,int ll,int rr,int l,int r,int v)
{
if(ll>rr)return;
if(l<=ll&&r>=rr)
{
tr[id].lazy+=v;return;
}
luo(id,ll,rr);int mid=(ll+rr)>>1;
if(r<=mid)change(id<<1,ll,mid,l,r,v);
else if(l>mid)change(id<<1|1,mid+1,rr,l,r,v);
else change(id<<1,ll,mid,l,mid,v),change(id<<1|1,mid+1,rr,mid+1,r,v);
}
inline int get(int id,int ll,int rr,int p)
{
if(ll==rr)return tr[id].lazy;
luo(id,ll,rr);int mid=(ll+rr)>>1;
if(p<=mid)return get(id<<1,ll,mid,p);
else return get(id<<1|1,mid+1,rr,p);
}
signed main()
{
int n,q;n=read(),q=read();
for(R int i=1;i<=n-1;i++)
{
int f=read(),w=read();
add(f,i+1,w);ww[i+1]=w;
}
d[1]=1;dfs(1);
for(int i=1;i<=tot;i++)change(1,1,tot,i,i,w[rk[i]]);
for(R int i=1;i<=q;i++)
{
int op=read();
if(op==1)
{
int x=read(),y=read();long long s=read();
int xx=get(1,1,tot,id[x]),yy=get(1,1,tot,id[y]);
int opt=(d[x]&1)+(d[y]&1);
if(opt==0)
{
long long ans=xx+yy-s;
if(ans&1)puts("none");
else printf("%lld\n",ans>>1);
continue;
}
if(opt==1)
{
if(d[x]&1)swap(x,y),swap(xx,yy);
long long ans=xx-yy;
if(ans==s)puts("inf");
else puts("none");
continue;
}
if(opt==2)
{
long long ans=xx+yy+s;
if(ans&1)puts("none");
else printf("%lld\n",ans>>1);
continue;
}
}
if(op==2)
{
int x=read(),w=read(),add;
if(d[fa[x]]&1)add=w-ww[x];
else add=ww[x]-w;
change(1,1,tot,id[x],id[x]+size[x]-1,add);
ww[x]=w;
}
}
return 0;
}
貌似是第一道考场打对的正解数据结构呢
T3.
好久的坑今天才填
坐标的值域不是很大,所以可以枚举值域
准备工作是把所有横坐标开vector,然后把对应的纵坐标往里扔,给每个vector排序
最好额外放进去一个2501,后面处理问题方便
然后枚举右端点\(R\),然后从右到左枚举左端点\(L\),跳过不合法(空)区间
像题解说的一样,考虑怎么计算出一个\(L\),\(R\)之间所有矩形面积
显然长固定为\(R-L\),想怎么算宽,每个矩形面积是\(S=(R-L)*(y_{max}-y_{min})\),将柿子拆开
借用sdfz大佬ycx的推导:
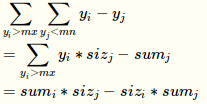
就变成了找符合条件的\(y_{max},y_{min}\)数量以及他们的和,用两个数状数组维护,一个往里插1,一个往里插纵坐标
从右向左枚举\(L\),把这个\(L\)的vector里的所有纵坐标插到\(R\)数状数组对应的位置,如果重了就不插
for(R int k=0;k<s[j].size();k++)
{
ll p=s[j][k];
if(!c[i].get(p,p))b[i].add(p,1),c[i].add(p,p);
}
这个插入的细节其实解决了横坐标相同的问题,关键的是纵坐标重了怎么办
如果纵坐标重了那么一个矩形可能会被计算多次,需要处理
可以分段处理,用类似扫描线的东西,本质上把它划分成了很多区间,分别计算贡献
维护上,中,下三条线,中,下范围是对应的区间,上线是上边界,下边界为1
具体实现先确定中线,然后下面最近的是下线,上线同理,用两个指针从小到大扫两个vector,看代码
还有记得卡常
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define R register
inline ll read()
{
ll x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
const ll mod=1e9+7,N=10050;
inline ll addmod(ll x,ll y){return x+y>=mod?x+y-mod:x+y;}
inline ll ganmod(ll x){return x-x/mod*mod;}
inline ll mulmod(ll x,ll y){return x*y-(x*y/mod)*mod;}
struct node{
ll x,y;
}a[N];
struct bit{
ll b[2505];
inline int lowbit(int x){return x&(-x);}
inline void add(int p,ll x)
{
for(R int i=p;i<=2501;i+=lowbit(i))
b[i]+=x;
}
inline ll getsum(int p)
{
ll s=0;
for(R int i=p;i;i-=lowbit(i))
s+=b[i];
return s;
}
inline ll get(int l,int r)
{
if(l>r)return 0;
return getsum(r)-getsum(l-1);
}
}b[2505],c[2505];
vector <ll> s[2505];
signed main()
{
int n=read();
for(R int i=1;i<=n;i++)
{
a[i].x=read(),a[i].y=read();
s[a[i].x].push_back(a[i].y);
b[a[i].x].add(a[i].y,1);
c[a[i].x].add(a[i].y,a[i].y);
}
for(R int i=1;i<=2500;i++)
{
s[i].push_back(2501);
sort(s[i].begin(),s[i].end());
}
ll ans=0;
for(R ll i=2500;i;i--)
{
if(s[i].size()==1)continue;
for(R ll j=i-1;j;j--)
{
if(s[j].size()==1)continue;
for(R int k=0;k<s[j].size();k++)
{
ll p=s[j][k];
if(!c[i].get(p,p))b[i].add(p,1),c[i].add(p,p);
}
int p1=0,p2=0;ll mid=max(s[i][p1],s[j][p2]);
while(s[i][p1+1]<=mid)p1++;
while(s[j][p2+1]<=mid)p2++;
while(p1<s[i].size()-1&&p2<s[j].size()-1)
{
ll r=min(s[i][p1+1],s[j][p2+1]);
ll l=min(s[i][p1],s[j][p2]);
ans=addmod(ans,mulmod((i-j),ganmod(c[i].get(mid,r-1)*b[i].get(1,l)-c[i].get(1,l)*b[i].get(mid,r-1))+mod));
mid=r;while(s[i][p1+1]<=mid)p1++;while(s[j][p2+1]<=mid)p2++;
}
}
}
printf("%lld\n",ans);
return 0;
}
考试总结
1.二分一定要注意边界!!!
2.适度卡常,有正解就把分拿到


 浙公网安备 33010602011771号
浙公网安备 33010602011771号