组合数学相关

二项式反演

若有两个长度均为\(n\)的数列\(f\),\(g\)，满足

\[g_m=\sum_{i=0}^m\dbinom{m}{i}f_i \]

则有

\[f_m=\sum_{i=0}^m(-1)^{m-i}\dbinom{m}{i}g_i \]

用途：有时对于较难求出的\(f\)，可利用其性质先求出\(g\),进而较为简单的求出\(f\)
至少形式（一般用的多）
若

\[g_m=\sum_{i=m}^{n}\dbinom{m}{i}f_i \]

就有

\[f_m=\sum_{i=m}^n(-1)^{i-m}\dbinom{m}{i}g_i \]

对第二个证明：（直接嫖学长的）

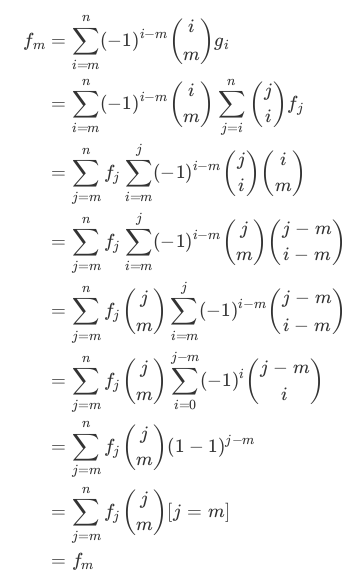
简单例题：
Bill的挑战
当时想了半天，把它换成至少然后反演一下随便切

范德蒙恒等式

\[C_{m+n}^k=\sum_{i=0}^mC_{m}^i\times C_{n}^{k-i} \]

作用：化简式子
特别说明：当求和项大于\(m\)时也成立，因为多出来的组合数不合法贡献为\(0\)

剩下各种反演咕了，因为根本不会