P2534

[AHOI2012]铁盘整理

题目描述

在训练中，一些臂力训练器材是少不了的，小龙在练习的时候发现举重器械上的铁盘放置的非常混乱，并没有按照从轻到重的顺序摆放，这样非常不利于循序渐进的锻炼。他打算利用一个非常省力气的办法来整理这些铁盘，即每次都拿起最上面的若干个圆盘并利用器械的力量上下翻转，这样翻转若干次以后，铁盘将会按照从小到大的顺序排列好。那么你能不能帮小龙确定，最少翻转几次就可以使铁盘按从小到大排序呢？

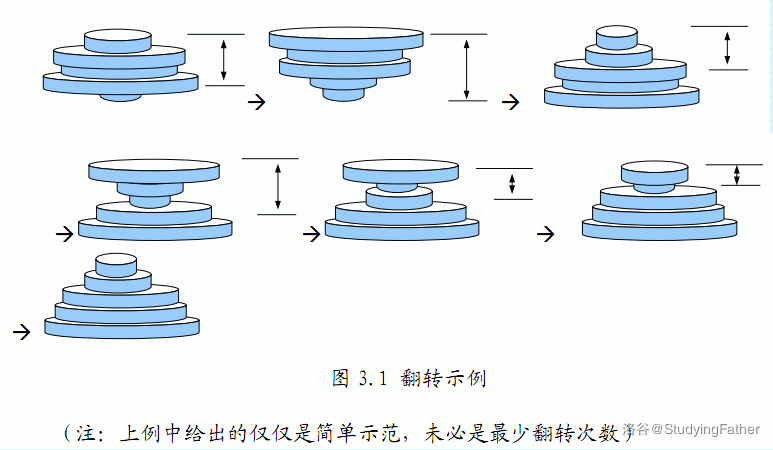
例如：下面的铁盘经过如图所示的以下几个步骤的翻转后变为从小到大排列。

输入格式

共两行。第一行为铁盘个数 \(N\)（\(1 \leq N \leq 16\)），第二行为 \(N\) 个不同的正整数，分别为从上到下的铁盘的半径 \(R\)（\(1 \leq R \leq 100\)）。

输出格式

一个正整数，表示使铁盘从小到大有序需要的最少翻转次数。

样例 #1

样例输入 #1

5
2 4 3 5 1

样例输出 #1

5

IDA* 迭代加深搜索
由于是求最少次数 要么BFS 要么IDA*
BFS的话重复状态判断是个难题（MLE）
所以IDA*
dfs(dep,pre,step)
dep:从0开始++
pre:上一次操作翻转1~pre
step:操作次数
IDA*最为重要的就是估价函数
这道题我们首先应该离散化
这样判断是否顺序合理只用判断abs(a[i+1]-a[i])==1
至于为什么不是(a[i+1]-a[i]!=1)就cnt++
我们估价要保守一点 宁可少剪枝 不要错！
像这种要求从小到大顺序排列的题目都可以试着离散化 判断更简单！

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,a[17],b[17],flag=0;
int cal()
{
	int cnt=0;
	for(int i=1;i<=n;i++)
		if(abs(a[i]-a[i+1])!=1)
			cnt++;
	return cnt;
}
void dfs(int dep,int pre,int step)
{
	if(flag)return ;
	int gj=cal();
	if(gj+step>dep)return ;
	if(gj==0)
	{
		flag=1;
		return ;
	}
	for(int i=2;i<=n;i++)
	{
		if(i==pre)continue;
		reverse(a+1,a+i+1);
		dfs(dep,i,step+1);
		reverse(a+1,a+i+1);
	}
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i],b[i]=a[i];
	sort(b+1,b+n+1);
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(b+1,b+n+1,a[i])-b;
	a[n+1]=n+1;
	for(int i=0;i<=20;i++)
	{
		flag=0;
		dfs(i,-1,0);
		if(flag)
		{
			cout<<i<<"\n";
			return 0;
		}
	}
	return 0;
}