P4799

[CEOI2015 Day2] 世界冰球锦标赛

题目描述

译自 CEOI2015 Day2 T1「Ice Hockey World Championship」

今年的世界冰球锦标赛在捷克举行。Bobek 已经抵达布拉格，他不是任何团队的粉丝，也没有时间观念。他只是单纯的想去看几场比赛。如果他有足够的钱，他会去看所有的比赛。不幸的是，他的财产十分有限，他决定把所有财产都用来买门票。

给出 Bobek 的预算和每场比赛的票价，试求：如果总票价不超过预算，他有多少种观赛方案。如果存在以其中一种方案观看某场比赛而另一种方案不观看，则认为这两种方案不同。

输入格式

第一行，两个正整数 \(N\) 和 \(M(1 \leq N \leq 40,1 \leq M \leq 10^{18})\)，表示比赛的个数和 Bobek 那家徒四壁的财产。

第二行，\(N\) 个以空格分隔的正整数，均不超过 \(10^{16}\)，代表每场比赛门票的价格。

输出格式

输出一行，表示方案的个数。由于 \(N\) 十分大，注意：答案 \(\le 2^{40}\)。

样例 #1

样例输入 #1

5 1000
100 1500 500 500 1000

样例输出 #1

8

提示

样例解释

八种方案分别是：

• 一场都不看，溜了溜了
• 价格 \(100\) 的比赛
• 第一场价格 \(500\) 的比赛
• 第二场价格 \(500\) 的比赛
• 价格 \(100\) 的比赛和第一场价格 \(500\) 的比赛
• 价格 \(100\) 的比赛和第二场价格 \(500\) 的比赛
• 两场价格 \(500\) 的比赛
• 价格 \(1000\) 的比赛

有十组数据，每通过一组数据你可以获得 10 分。各组数据的数据范围如下表所示：

数据组号	\(1-2\)	\(3-4\)	\(5-7\)	\(8-10\)
\(N \leq\)	\(10\)	\(20\)	\(40\)	\(40\)
\(M \leq\)	\(10^6\)	\(10^{18}\)	\(10^6\)	\(10^{18}\)

折半搜索 meet in the middle
由于M的范围 不能用背包解决 所以只能搜索 用DFS带着传递的sum来求
由于N>=40 直接搜索TLE 所以折半搜索 复杂度降低为2^(N/2+1)
折半搜索原理：

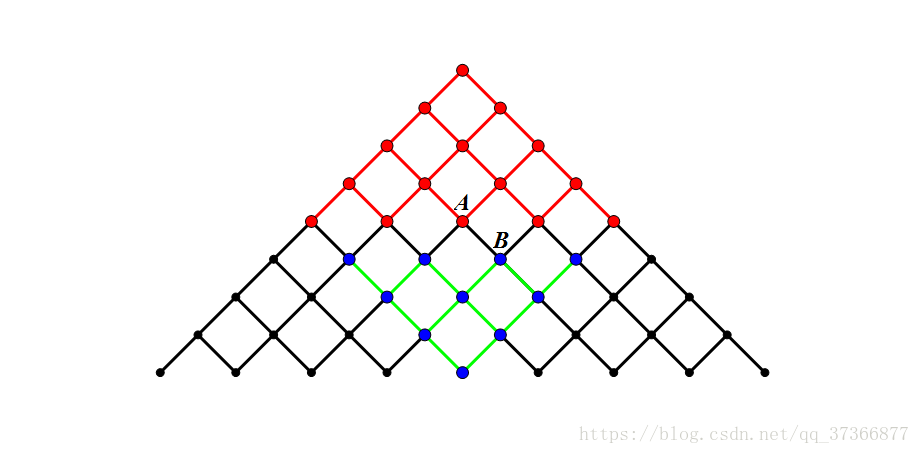
我们分别dfs(1,mid,0,cnta,a[]) dfs(mid+1,n,0,cntb,b[])
得到了a[] b[] 里面有所有总和不超过m的组合
我们sort(a+1,a+cnta+1) 然后对于每一个b[i] 在a[]中查找 upper_bound m-b[i]
找到pos 那么对于pos之前的a[j] 均有a[j]+b[i]<=m 直接累加pos-1即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int n;
ll m,c[45],a[1<<21],b[1<<21],cnta,cntb;
void dfs(int l,int r,ll sum,ll& cnt,ll arr[])
{
	if(sum>m)return ;
	if(l>r)
	{
		arr[++cnt]=sum;
		return ;
	}
	dfs(l+1,r,sum,cnt,arr);
	dfs(l+1,r,sum+c[l],cnt,arr);
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>c[i];
	int mid=(1+n)>>1;
	dfs(1,mid,0,cnta,a);
	dfs(mid+1,n,0,cntb,b);
	sort(a+1,a+cnta+1);
	ll tot=0;
	for(int i=1;i<=cntb;i++)
		tot+=(upper_bound(a+1,a+cnta+1,m-b[i])-a)-1;
	cout<<tot<<"\n";
	return 0;
}