P1351

[NOIP2014 提高组] 联合权值

题目描述

无向连通图 \(G\) 有 \(n\) 个点，\(n-1\) 条边。点从 \(1\) 到 \(n\) 依次编号,编号为 \(i\) 的点的权值为 \(W_i\)，每条边的长度均为 \(1\)。图上两点 \((u, v)\) 的距离定义为 \(u\) 点到 \(v\) 点的最短距离。对于图 \(G\) 上的点对 \((u, v)\)，若它们的距离为 \(2\)，则它们之间会产生\(W_v \times W_u\) 的联合权值。

请问图 \(G\) 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入格式

第一行包含 \(1\) 个整数 \(n\)。

接下来 \(n-1\) 行,每行包含 \(2\) 个用空格隔开的正整数 \(u,v\)，表示编号为 \(u\) 和编号为 \(v\) 的点之间有边相连。

最后 \(1\) 行,包含 \(n\) 个正整数，每两个正整数之间用一个空格隔开，其中第 \(i\) 个整数表示图 \(G\) 上编号为 \(i\) 的点的权值为 \(W_i\)。

输出格式

输出共 \(1\) 行,包含 \(2\) 个整数，之间用一个空格隔开,依次为图 \(G\) 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对\(10007\)取余。

样例 #1

样例输入 #1

5  
1 2  
2 3
3 4  
4 5  
1 5 2 3 10

样例输出 #1

20 74

提示

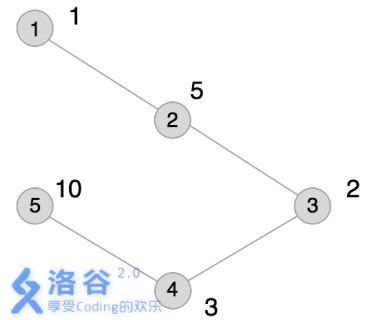
本例输入的图如上所示，距离为2 的有序点对有\(( 1,3)\) 、\(( 2,4)\) 、\(( 3,1)\) 、$( 3,5) \(、\)( 4,2)$ 、$( 5,3) $。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30%的数据，\(1 < n \leq 100\)；

对于60%的数据，\(1 < n \leq 2000\)；

对于100%的数据，\(1 < n \leq 200000, 0 < W_i \leq 10000\)。

保证一定存在可产生联合权值的有序点对。

好题！！！
距离为2 两种情况
1.u&&grandfather
2.u&&fa's other son
DFS(u,fa,graf)
对于第二种情况 最大值肯定是fa儿子中最大和次大的乘积
至于tot的更新 +=2*Πaiaj  =(a1+…+ai)^2-(a1^2+…+ai^2)所以维护即可
树形DP一遍DFS搞定

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long 
int n;
struct Tree{
	int nxt,to;
}edge[200005*2];
int head[200005*2],cnt;
void add(int u,int v)
{
	cnt++;
	edge[cnt].nxt=head[u];
	edge[cnt].to=v;
	head[u]=cnt;
}
const int mod=10007;
int a[200005],maxx=-INT_MAX,tot=0;
void DFS(int u,int fa,int graf)
{
	int max1=0,max2=0,s1=0,s2=0;	
	for(int i=head[u];i;i=edge[i].nxt)
	{
		int v=edge[i].to;
		if(v==fa)continue;
		s1=(s1+a[v])%mod;
		s2=(s2+a[v]*a[v]%mod)%mod;
		if(a[v]>max1)
			max2=max1,max1=a[v];
		else if(a[v]>max2)max2=a[v];
		DFS(v,u,fa);
	}
	maxx=max(maxx,max(max1*max2,a[u]*a[graf]));
	tot=(tot+(s1*s1%mod-s2+mod)%mod+2*a[u]*a[graf]%mod)%mod;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	for(int i=1;i<n;i++)
	{
		int u,v;
		cin>>u>>v;
		add(u,v);
		add(v,u);
	}
	for(int i=1;i<=n;i++)cin>>a[i];
	DFS(1,0,0);
	cout<<maxx<<" "<<tot<<"\n";
	return 0;
}