P3373

【模板】线段树 2

题目描述

如题，已知一个数列，你需要进行下面三种操作：

• 将某区间每一个数乘上 \(x\)

• 将某区间每一个数加上 \(x\)

• 求出某区间每一个数的和

输入格式

第一行包含三个整数 \(n,m,p\)，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 \(n\) 个用空格分隔的整数，其中第 \(i\) 个数字表示数列第 \(i\) 项的初始值。

接下来 \(m\) 行每行包含若干个整数，表示一个操作，具体如下：

操作 \(1\)： 格式：1 x y k 含义：将区间 \([x,y]\) 内每个数乘上 \(k\)

操作 \(2\)： 格式：2 x y k 含义：将区间 \([x,y]\) 内每个数加上 \(k\)

操作 \(3\)： 格式：3 x y 含义：输出区间 \([x,y]\) 内每个数的和对 \(p\) 取模所得的结果

输出格式

输出包含若干行整数，即为所有操作 \(3\) 的结果。

样例 #1

样例输入 #1

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

样例输出 #1

17
2

提示

【数据范围】

对于 \(30\%\) 的数据：\(n \le 8\)，\(m \le 10\)
对于 \(70\%\) 的数据：$n \le 10^3 \(，\) m \le 10^4$
对于 \(100\%\) 的数据：$ n \le 10^5\(，\) m \le 10^5$

除样例外，\(p = 571373\)

（数据已经过加强^_）

样例说明：

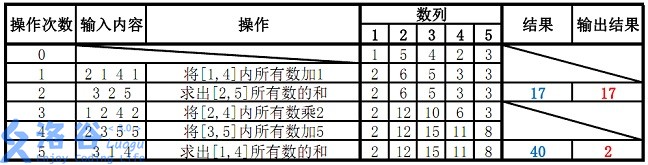
故输出应为 \(17\)、\(2\)（ \(40 \bmod 38 = 2\) ）

注意 先×后＋

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,mod,x,y,k;
struct tree{
	int l,r,sum,add,mul;
}tr[100005*4];
int a[100005*4];
void pushup(int p)
{
	tr[p].sum=tr[p<<1].sum+tr[p<<1|1].sum;
	tr[p].sum%=mod;
}
void build(int p,int l,int r)
{
	tr[p].l=l,tr[p].r=r;tr[p].add=0,tr[p].mul=1;
	if(l==r)
	{
		tr[p].sum=a[l];
		return ;
	}
	int mid=(l+r)>>1;	
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	pushup(p);
}
void eval(tree& t,int mul,int add)
{
	t.sum=(t.sum*mul+(t.r-t.l+1)*add)%mod;
	t.mul=t.mul*mul;t.mul%=mod;
	t.add=t.add*mul+add;t.add%=mod;
}
void pushdown(int p)
{
	eval(tr[p<<1],tr[p].mul,tr[p].add);
	eval(tr[p<<1|1],tr[p].mul,tr[p].add);
	tr[p].add=0,tr[p].mul=1;
}
void modify(int p,int l,int r,int mul,int add	)
{
	if(l<=tr[p].l&&r>=tr[p].r)
	{
		eval(tr[p],mul,add);
		return ;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)modify(p<<1,l,r,mul,add);
	if(r>mid)modify(p<<1|1,l,r,mul,add);
	pushup(p);
}
int query(int p,int l,int r)
{
	if(l<=tr[p].l&&r>=tr[p].r)
	{
		return tr[p].sum;
	}
	pushdown(p);
	int sum=0;
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)sum=(sum+query(p<<1,l,r));
	if(r>mid)sum=(sum+query(p<<1|1,l,r));
	return sum%mod;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m>>mod;
	for(int i=1;i<=n;i++)cin>>a[i];
	build(1,1,n);
	while(m--)
	{
		int op;
		cin>>op;
		if(op==1)
		{
			cin>>x>>y>>k;
			modify(1,x,y,k,0);
		}
		if(op==2)
		{
			cin>>x>>y>>k;
			modify(1,x,y,1,k);
		}
		if(op==3)
		{
			cin>>x>>y;
			cout<<(query(1,x,y)+mod)%mod<<"\n";
		}
	}
	return 0;
}