P5057

[CQOI2006]简单题

题目描述

有一个 n 个元素的数组，每个元素初始均为 0。有 m 条指令，要么让其中一段连续序列数字反转——0 变 1，1
变 0（操作 1），要么询问某个元素的值（操作 2）。
例如当 n = 20 时，10 条指令如下：

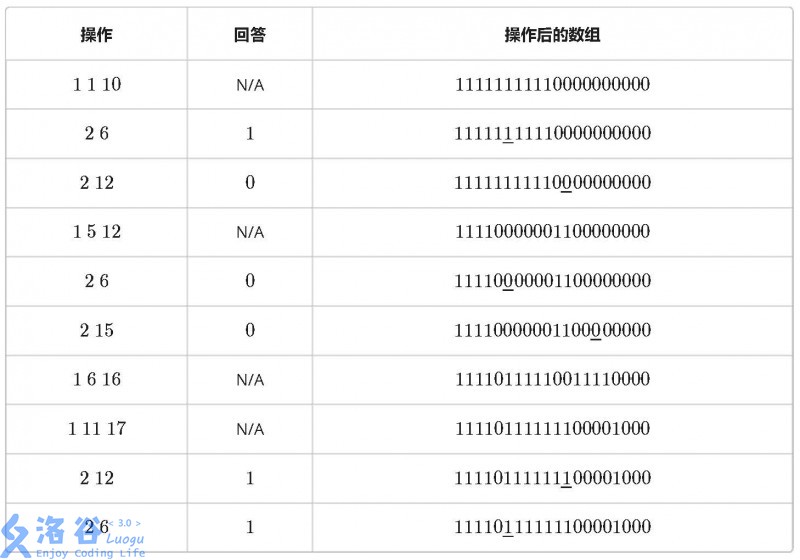
输入格式

第一行包含两个整数 n, m，表示数组的长度和指令的条数； 以下 m 行，每行的第一个数 t 表示操作的种类：

若 t = 1，则接下来有两个数 L, R，表示区间 [L, R] 的每个数均反转； 若 t = 2，则接下来只有一个数 i，表示询问的下标。

输出格式

每个操作 2 输出一行（非 0 即 1），表示每次操作 2 的回答。

样例 #1

样例输入 #1

20 10
1 1 10
2 6
2 12
1 5 12
2 6
2 15
1 6 16
1 11 17
2 12
2 6

样例输出 #1

1
0
0
0
1
1

提示

对于 50% 的数据，1 ≤ n ≤ \(10^3\), 1 ≤ m ≤ \(10^4\)；
对于 100% 的数据，1 ≤ n ≤ \(10^5\), 1 ≤ m ≤ 5 × \(10^5\)，保证 L ≤ R。

线段树的一种变形
这种我们只用记录每个区间翻转了多少次
用add记录即可 每次反转+1 最后若为奇数则为1 否则为0
所以这个query是tot+=add

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,a[100005],m;
struct tree{
	int l,r,sum,add;
}tr[100005*4];
void pushup(int p)
{
	tr[p].sum=tr[p<<1].sum+tr[p<<1|1].sum;
}
void build(int p,int l,int r)
{
	tr[p].l=l,tr[p].r=r;
	if(l==r)
	{
		tr[p].sum=0;
		return ;	
	} 
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	pushup(p);
}
void pushdown(int p)
{
	tr[p<<1].sum+=tr[p].add*(tr[p<<1].r-tr[p<<1].l+1);
	tr[p<<1].add+=tr[p].add;
	tr[p<<1|1].sum+=tr[p].add*(tr[p<<1|1].r-tr[p<<1|1].l+1);
	tr[p<<1|1].add+=tr[p].add;
	tr[p].add=0;
}
void modify(int p,int l,int r,int k)
{
	if(l<=tr[p].l&&r>=tr[p].r)
	{
		tr[p].add+=k;
		tr[p].sum+=k*(tr[p].r-tr[p].l+1);
		return ;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)modify(p<<1,l,r,k);
	if(r>mid)modify(p<<1|1,l,r,k);
	pushup(p);
}
int query(int p,int l,int r)
{
	if(l<=tr[p].l&&r>=tr[p].r)
	{
		return tr[p].add;
	}
	pushdown(p);
	int tot=0;
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)tot+=query(p<<1,l,r);
	if(r>mid)tot+=query(p<<1|1,l,r);
	return tot;
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	build(1,1,n);
	while(m--)
	{
		int op,x,y;
		cin>>op;
		if(op==1)
		{
			cin>>x>>y;
			
			modify(1,x,y,1);
		}
		else
		{
			cin>>x;
			cout<<query(1,x,x)%2<<"\n";
		}
	}
	return 0;
}