P1886

滑动窗口 /【模板】单调队列

题目描述

有一个长为 \(n\) 的序列 \(a\)，以及一个大小为 \(k\) 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is \([1,3,-1,-3,5,3,6,7]\), and \(k = 3\)。

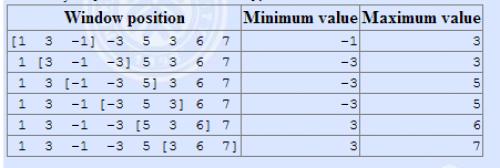
输入格式

输入一共有两行，第一行有两个正整数 \(n,k\)。
第二行 \(n\) 个整数，表示序列 \(a\)

输出格式

输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值

样例 #1

样例输入 #1

8 3
1 3 -1 -3 5 3 6 7

样例输出 #1

-1 -3 -3 -3 3 3
3 3 5 5 6 7

提示

【数据范围】
对于 \(50\%\) 的数据，\(1 \le n \le 10^5\)；
对于 \(100\%\) 的数据，\(1\le k \le n \le 10^6\)，\(a_i \in [-2^{31},2^{31})\)。

单调队列模板题 虽说我打线段树不好吗…
以最小值为例：若当前a[i]不大于队首a[q[r]] 
那么a[q[r]]永远不可能成为最小值了 所以r--直到a[i]入队后最小
然后维护区间长度为k即可 只需l++

单调队列维护的都是a[q[l]]为最大/最小值

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,k,a[1000005];
struct tree{
	int l,r,minn,maxx;
}tr[1000005*4];
void pushup(int p)
{
	tr[p].maxx=max(tr[p<<1].maxx,tr[p<<1|1].maxx);
	tr[p].minn=min(tr[p<<1].minn,tr[p<<1|1].minn);
}
void build(int p,int l,int r)
{
	tr[p].l=l,tr[p].r=r;
	if(l==r)
	{
		tr[p].maxx=a[l];
		tr[p].minn=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	pushup(p);
}
int query1(int p,int l,int r)
{
	int maxx=-LONG_MAX;
	if(l<=tr[p].l&&r>=tr[p].r)
		return tr[p].maxx;
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)maxx=max(maxx,query1(p<<1,l,r));
	if(r>mid)maxx=max(maxx,query1(p<<1|1,l,r));
	return maxx;
}
int query2(int p,int l,int r)
{
	int minn=LONG_MAX;
	if(l<=tr[p].l&&r>=tr[p].r)
		return tr[p].minn;
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)minn=min(minn,query2(p<<1,l,r));
	if(r>mid)minn=min(minn,query2(p<<1|1,l,r));
	return minn;
}
int q[1000005],l=1,r=0;
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)
	{
		while(l<=r&&a[q[r]]>=a[i])
			r--;
		q[++r]=i;
		while(q[r]-q[l]+1>k)
			l++;
		if(i>=k)cout<<a[q[l]]<<" ";
	}
	cout<<"\n";
	l=1,r=0;memset(q,0,sizeof(q));
	for(int i=1;i<=n;i++)
	{
		while(l<=r&&a[q[r]]<=a[i])
			r--;
		q[++r]=i;
		while(q[r]-q[l]+1>k)
			l++;
		if(i>=k)cout<<a[q[l]]<<" ";
	}
	return 0;
}