P1436

棋盘分割

题目背景

无

题目描述

将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

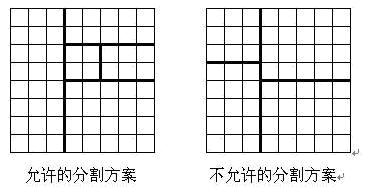
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及n，求出平方和的最小值。

输入格式

第1行为一个整数n(1 < n <= 15)。

第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式

仅一个数，为平方和。

样例 #1

样例输入 #1

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

样例输出 #1

1460

搜索+记忆化
but 我因为根据前缀和求权值矩形和的公式写错调了0.5h…
(x1,y1)~(x2,y2):
s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]
然后开个f[sx][sy][tx][ty][step]:矩形为(sx,sy)~(tx,ty)且为第step步时的最小值
if(tot>=f[sx][sy][tx][ty][step])return ;

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,a[10][10],s[10][10],minn=INT_MAX;
int f[15][15][15][15][20];
int pf(int x)
{
	return x*x;
}
void dfs(int sx,int sy,int tx,int ty,int step,int tot)
{
//	printf("(%d,%d)  (%d,%d)   %d   %d\n",sx,sy,tx,ty,step,tot);
	if(step==n)
	{
		tot+=pf(s[tx][ty]-s[tx][sy-1]-s[sx-1][ty]+s[sx-1][sy-1]);
		minn=min(minn,tot);
		return ;
	}
	if(tot>=minn)return ;
//	if(tot>f[step])return ;
	if(tot>=f[sx][sy][tx][ty][step])return ;
	f[sx][sy][tx][ty][step]=min(f[sx][sy][tx][ty][step],tot);
	for(int i=sy;i<=ty;i++)
	{
		dfs(sx,sy,tx,i,step+1,tot+pf(s[tx][ty]-s[tx][i]-s[sx-1][ty]+s[sx-1][i]));
		dfs(sx,i+1,tx,ty,step+1,tot+pf(s[tx][i]-s[tx][sy-1]-s[sx-1][i]+s[sx-1][sy-1]));
	}
	for(int i=sx;i<=tx;i++)
	{
		dfs(sx,sy,i,ty,step+1,tot+pf(s[tx][ty]-s[tx][sy-1]-s[i][ty]+s[i][sy-1]));
		dfs(i+1,sy,tx,ty,step+1,tot+pf(s[i][ty]-s[i][sy-1]-s[sx-1][ty]+s[sx-1][sy-1]));
	}
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>n;
	memset(f,0x3f,sizeof(f));
	for(int i=1;i<=8;i++)
		for(int j=1;j<=8;j++)
			cin>>a[i][j],s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
	dfs(1,1,8,8,1,0);
	cout<<minn<<"\n";
	return 0;
}
/*
2
1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1
*/