P5003

跳舞的线 - 乱拐弯

题目背景

线初始面对方向请自己确定

题目描述

线现在在一个地图上，它正在 \((1,1)\) 上（左上角），最终要去到 \((M,N)\) 上。它不但只能往下或往右走，还只能在整数格子上移动。

Imakf 有的时候想要炫技，又有时想偷懒，所以他会告诉你这张地图的全貌，你要告诉他到达终点的最多和最少拐弯次数。

输入格式

第一行两个正整数 \(M,N\)，意义见题目描述。

第 \(2\sim M+1\) 行，每行 \(N\) 个字符。如果为 # 就代表这里有障碍，反之没有。

输出格式

输出两个正整数 \(max,min\)，\(max\) 表示最多拐弯次数，\(min\) 表示最少拐弯次数。

如果到达不了就仅输出 -1。

样例 #1

样例输入 #1

5 5
oooo#
ooooo
#oo#o
o#ooo
oo#oo

样例输出 #1

7 2

样例 #2

样例输入 #2

5 5
oooo#
ooooo
#oo##
o#o#o
oo#oo

样例输出 #2

-1

提示

样例 \(1\) 说明：

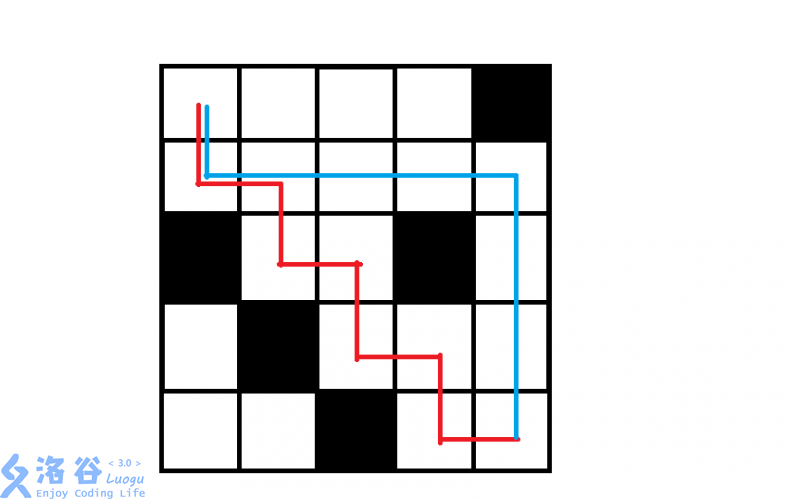
红色路线代表拐弯次数最多。

蓝色路线代表拐弯次数最少。

---

样例 \(2\) 说明：

显然过不去。

\(1\le M,N\le 1000\)

撡
我TMD会写最大值的DP但是不会写最小值的（写挂了）
所以求最大拐弯用DP 最小用DFS+剪枝

重点 剪枝部分

首先是基本的几个最优性剪枝：
ans_now>=ans return

还有记忆化类型的！！！

1.g[x][y]:(x,y)目前搜到的最小值
2.vis[x][y][op]:（x,y）方向为op是否搜过
注意剪枝时是ans_now>g[x][y] return 等于g[x][y]时不一定！
有可能是不同方向来的有更优解
所以 ans_now==g[x][y]&&vis[x][y][op] return

最后 不要忘了对起点是'#'的特判！！！

Code

#include<bits/stdc++.h>//
using namespace std;
#define int long long
int n,m;
char ch[1005][1005];
int f[1005][1005][2],g[1005][1005],ans1,ans2=INT_MAX,flag=0,cs=0,vis[1005][1005][2];
void dfs(int x,int y,int cnt,int fx)
{
//	cs++;
	
	if(x==n&&y==m)
	{
		flag=1;
		ans2=min(ans2,cnt);
		return ;
	}
//	if(x<n&&y<m&&cnt+1>=ans2)return ;
	
	if(cnt>=ans2)return ;
	if(cnt>g[x][y])return ;
	if(cnt==g[x][y]&&vis[x][y][fx])return ;
//	if(vis[x][y][fx])return ;
	vis[x][y][fx]=1;
	g[x][y]=min(g[x][y],cnt);
	if(x+1<=n&&ch[x+1][y]!='#')
	{
		if(x==1&&y==1)fx=1;
		if(fx==0)dfs(x+1,y,cnt+1,1);
		else dfs(x+1,y,cnt,1);
	}
	if(y+1<=m&&ch[x][y+1]!='#')
	{
		if(x==1&&y==1)fx=0;
		if(fx==1)dfs(x,y+1,cnt+1,0);
		else dfs(x,y+1,cnt,0);
	}
}
signed main()
{
	ios::sync_with_stdio(false);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin>>ch[i][j];
	if(ch[1][1]=='#')
	{
		cout<<-1<<"\n";
		return 0;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			if(ch[i][j]=='#')continue;
			if(ch[i-1][j]=='#'&&ch[i][j-1]=='o')
			{
				f[i][j][0]=max(f[i][j][0],f[i][j-1][1]+1);
			}
			if(ch[i][j-1]=='#'&&ch[i-1][j]=='o')
			{
				f[i][j][1]=max(f[i][j][1],f[i-1][j][0]+1);
			}
			if(ch[i-1][j]=='o')f[i][j][1]=max(f[i][j][1],max(f[i-1][j][0],f[i-1][j][1]));
			if(ch[i][j-1]=='o')f[i][j][0]=max(f[i][j][0],max(f[i][j-1][0],f[i][j-1][1]));
			if(ch[i-1][j]=='o'&&ch[i][j-1]=='o'&&ch[i-1][j-1]=='o')
			{
				f[i][j][0]=max(f[i][j][0],f[i][j-1][1]+1);
				f[i][j][1]=max(f[i][j][1],f[i-1][j][0]+1);
			}
		}
	
	ans1=max(f[n][m][0],f[n][m][1]);
	memset(g,0x3f,sizeof(g));
	dfs(1,1,0,0);
	if(!flag)
	{
		cout<<-1<<"\n";
		return 0;
	}
	cout<<ans1<<" "<<ans2<<"\n";
	return 0;
}