P3956

[NOIP2017 普及组] 棋盘

题目背景

NOIP2017 普及组 T3

题目描述

有一个\(m \times m\)的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的）， 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 $1 $个金币。

另外， 你可以花费 \(2\) 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用， 而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法； 只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入格式

第一行包含两个正整数$ m, n$，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的$ n \(行，每行三个正整数\) x, y, c\(， 分别表示坐标为\)(x,y)\(的格子有颜色\) c$。

其中$ c=1$ 代表黄色，$ c=0$ 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为\((1, 1)\)，右下角的坐标为\(( m, m)\)。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是\((1, 1)\) 一定是有颜色的。

输出格式

一个整数，表示花费的金币的最小值，如果无法到达，输出\(-1\)。

样例 #1

样例输入 #1

5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0

样例输出 #1

8

样例 #2

样例输入 #2

5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0

样例输出 #2

-1

提示

输入输出样例 1 说明

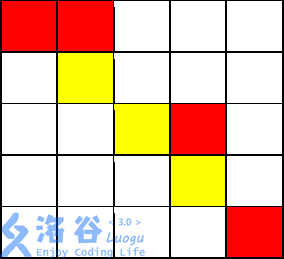
从\((1,1)\)开始，走到\((1,2)\)不花费金币

从\((1,2)\)向下走到\((2,2)\)花费 \(1\) 枚金币

从\((2,2)\)施展魔法，将\((2,3)\)变为黄色，花费 \(2\) 枚金币

从\((2,2)\)走到\((2,3)\)不花费金币

从\((2,3)\)走到\((3,3)\)不花费金币

从\((3,3)\)走到\((3,4)\)花费 \(1\) 枚金币

从\((3,4)\)走到\((4,4)\)花费 \(1\) 枚金币

从\((4,4)\)施展魔法，将\((4,5)\)变为黄色，花费$ 2$ 枚金币，

从\((4,4)\)走到\((4,5)\)不花费金币

从\((4,5)\)走到\((5,5)\)花费 \(1\) 枚金币

共花费 $8 $枚金币。

输入输出样例 2 说明

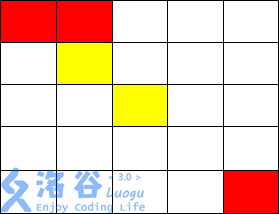
从\(( 1, 1)\)走到\(( 1, 2)\),不花费金币

从\(( 1, 2)\)走到\(( 2, 2)\),花费$ 1 $金币

施展魔法将\(( 2, 3)\)变为黄色,并从\(( 2, 2)\)走到\(( 2, 3)\)花费$ 2$ 金币

从\(( 2, 3)\)走到\(( 3, 3)\)不花费金币

从\(( 3, 3)\)只能施展魔法到达\(( 3, 2),( 2, 3),( 3, 4),( 4, 3)\)

而从以上四点均无法到达\(( 5, 5)\),故无法到达终点,输出\(-1\)

数据规模与约定

对于 \(30\%\)的数据, \(1 ≤ m ≤ 5, 1 ≤ n ≤ 10\)。

对于 \(60\%\)的数据, \(1 ≤ m ≤ 20, 1 ≤ n ≤ 200\)。

对于 \(100\%\)的数据, \(1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000\)。

---

一个常见的记忆化搜索技巧：
d[x][y]:目前为止搜到的走到(x,y)的最小cost

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int m,n;
int a[105][105],minn=2*105*105,d[105][105];
int vis[105][105];
int dx[4]={1,0,-1,0};
int dy[4]={0,1,0,-1};
int flag=0;
void dfs(int x,int y,int cost,int used)
{
//	cout<<x<<" "<<y<<"\n";
	if(cost>=d[x][y])return ;
	d[x][y]=min(d[x][y],cost);
	if(cost>=minn)return ;
	if(x==m&&y==m)
	{
		flag=1;
		minn=min(minn,cost);
		return ;
	}
	for(int i=0;i<4;i++)
	{
		int nx=x+dx[i],ny=y+dy[i];
		if(nx>m||ny>m||nx<1||ny<1)continue;
		if(vis[nx][ny])continue;
		if(a[nx][ny]==-1)
		{
			if(!used)
			{
				a[nx][ny]=a[x][y];
				vis[nx][ny]=1;
				dfs(nx,ny,cost+2,1);
				vis[nx][ny]=0;
				a[nx][ny]=-1;
			}
		}
		else
		{
			if(used)used=0;
			if(a[nx][ny]==a[x][y])
			{
				vis[nx][ny]=1;
				dfs(nx,ny,cost,used);
				vis[nx][ny]=0;
			}
			else
			{
				vis[nx][ny]=1;
				dfs(nx,ny,cost+1,used);
				vis[nx][ny]=0;
			}
		}
		
	}
	return ;
}
int main()
{
	ios::sync_with_stdio(false);
	cin>>m>>n;
	memset(d,0x3f,sizeof(d));
	memset(a,-1,sizeof(a));
	for(int i=1;i<=n;i++)
	{
		int x,y,c;
		cin>>x>>y>>c;
		a[x][y]=c;
	}
//	for(int i=1;i<=m;i++)
//	{
//		for(int j=1;j<=m;j++)
//			cout<<a[i][j]<<" ";
//		cout<<"\n";
//	}
	vis[1][1]=1;
	dfs(1,1,0,0);
	if(flag)cout<<minn<<"\n";
	else cout<<-1<<"\n";
	return 0;
}