博客作业06--图
1.学习总结
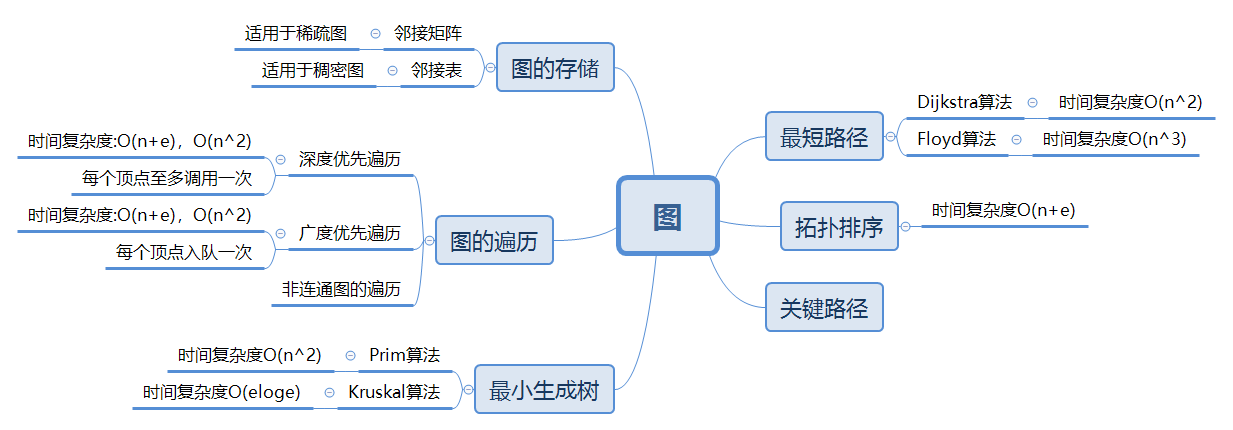
1.1图的思维导图
1.2 图结构学习体会
- 深度优先遍历：从顶点v出发，以纵向方式一步一步向后访问各个顶点。查找所有顶点的所有邻接点所需时间为O(n2)，n为顶点数，算法时间复杂度为O(n²)
- 广度优先遍历：从顶点v出发，以横向方式一步一步向后访问各个顶点。查找每个顶点的邻接点所需时间为O(n2)，n为顶点数，算法的时间复杂度为O(n²)
- Prim算法： 时间复杂度为O（n²）
- Kruscal算法：时间复杂度：O(e²)
- Dijkstra算法：时间复杂度：O(n²) 堆优化后O(nlogn)
- 拓扑排序算法：时间复杂度：O(n²)
2.PTA实验作业
2.1 题目1：7-1 图着色问题
2.2 设计思路
vector<int>Q[501];
for i=0 to e
输入ab，Q[a].push_back(b),Q[b].push_back(a);
while sum--
s.clear();
for i=1 to v
输入color[i];
s.insert(color[i]);
for i=1 to v
for j=0 to Q[i].size()
如果color[i]==color[Q[i][j]]
flag置0，结束循环
如果flag==0 结束循环
如果flag==1 输出Yes，否则输出No
2.3 代码截图
2.4 PTA提交列表说明
- 无问题
2.1 题目1：7-2 排座位
2.2 设计思路
for i=0 to M
输入abs
friends[a][b]=s;
friends[b][a]=s;
for i=0 to K
若friends[a][b]==1，输出No problem
flag=0;
vis[a][b]=vis[b][a]=1;
VIS(a,b);
若friends[a][b]==-1
如果flag==1 输出OK but...
否则输出No way
否则
如果flag==1 输出No problem
否则输出OK
2.3 代码截图
2.4 PTA提交列表说明
- 无问题
2.1 题目1：7-3 六度空间
2.2 设计思路
for i=0 to k
输入ab
a--;b--;
G[a][b]=G[b][a]=1;
for i=0 to N
for j=0 to N
visited[j]=0;
num=BFS(i);
um=num*1.0/N*100;
输出i+1,sum
2.3 代码截图
2.4 PTA提交列表说明
- 无问题
3.截图本周题目集的PTA最后排名
3.1 PTA排名
3.2 我的总分：250
4. 阅读代码
- 计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出，它的优势在于在对于较小范围内的整数排序。它的复杂度为Ο(n+k)（其中k是待排序数的范围），快于任何比较排序算法，缺点就是非常消耗空间。很明显，如果而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序，比如堆排序和归并排序和快速排序。
- 算法原理： 基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，在代码中作适当的修改即可。
- 算法步骤：
（1）找出待排序的数组中最大的元素；
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。 - 时间复杂度：Ο(n+k)。
- 空间复杂度：Ο(k)。
- 要求：待排序数中最大数值不能太大。
- 稳定性：稳定。
#define MAXNUM 20 //待排序数的最大个数
#define MAX 100 //待排序数的最大值
int sorted_arr[MAXNUM]={0};
//计算排序
//arr:待排序数组，sorted_arr：排好序的数组，n：待排序数组长度
void countSort(int *arr, int *sorted_arr, int n)
{
int i;
int *count_arr = (int *)malloc(sizeof(int) * (MAX+1));
//初始化计数数组
memset(count_arr,0,sizeof(int) * (MAX+1));
//统计i的次数
for(i = 0;i<n;i++)
count_arr[arr[i]]++;
//对所有的计数累加，作用是统计arr数组值和小于小于arr数组值出现的个数
for(i = 1; i<=MAX; i++)
count_arr[i] += count_arr[i-1];
//逆向遍历源数组（保证稳定性），根据计数数组中对应的值填充到新的数组中
for(i = n-1; i>=0; i--)
{
//count_arr[arr[i]]表示arr数组中包括arr[i]和小于arr[i]的总数
sorted_arr[count_arr[arr[i]]-1] = arr[i];
//如果arr数组中有相同的数，arr[i]的下标减一
count_arr[arr[i]]--;
}
free(count_arr);
}
