代码随想录算法训练营第52天 | 图论基础1

图论理论基础
https://www.programmercarl.com/kamacoder/图论理论基础.html#图的基本概念
深度优先搜索理论基础
https://www.programmercarl.com/kamacoder/图论深搜理论基础.html#深搜三部曲
98.所有可达路径
https://kamacoder.com/problempage.php?pid=1170
代码随想录
https://www.programmercarl.com/kamacoder/0098.所有可达路径.html
广度优先搜索理论基础
https://www.programmercarl.com/kamacoder/图论广搜理论基础.html

图论基础

• 图种类

  • 有向图和无向图；
  • 加权无向图和加权有向图；

• 度

  • 无向图：边的个数
  • 有向图：入度（指向该节点的个数） 和 出入 （从该节点出发的个数）

• 连通性

  • 无向图-连通图：任何节点都可以达到；
  • 有向图- 强连通图：任何两个节点可以互相达到；

• 连通分量

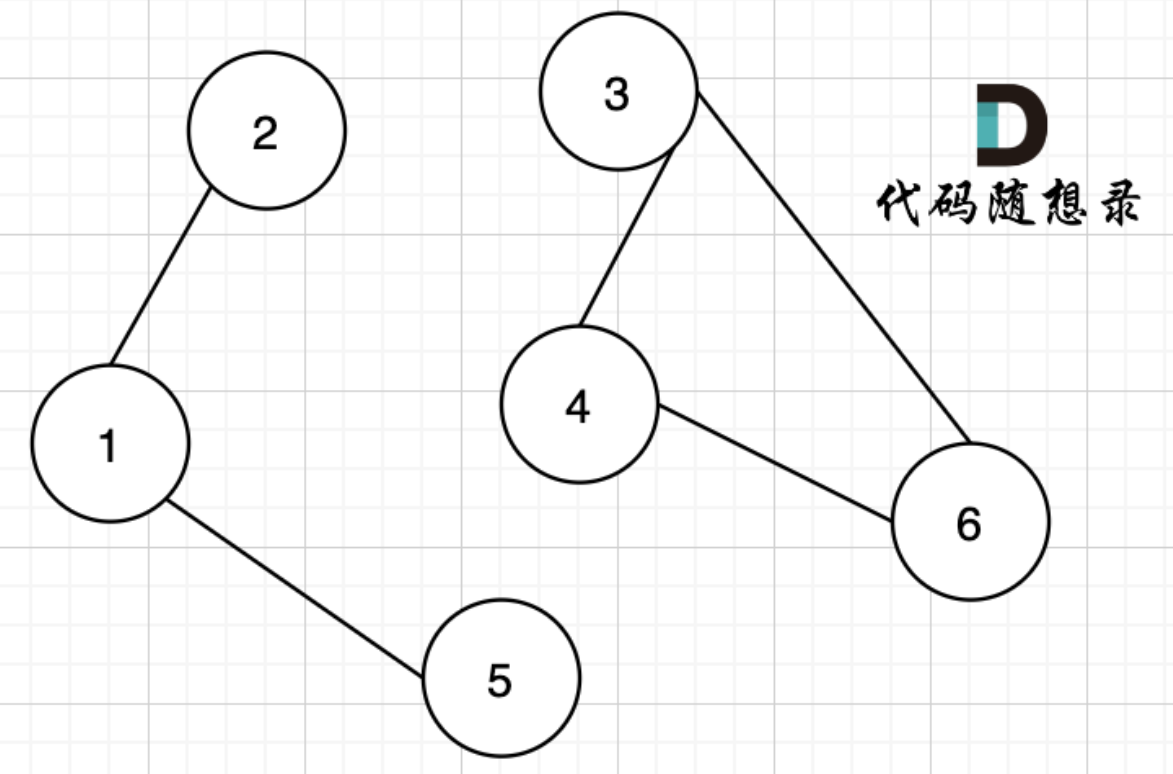
  • 在无向图中：极大连通子图就是该图的连通分量；如下图的（1,2,5）节点和（3,4,6）节点；
    
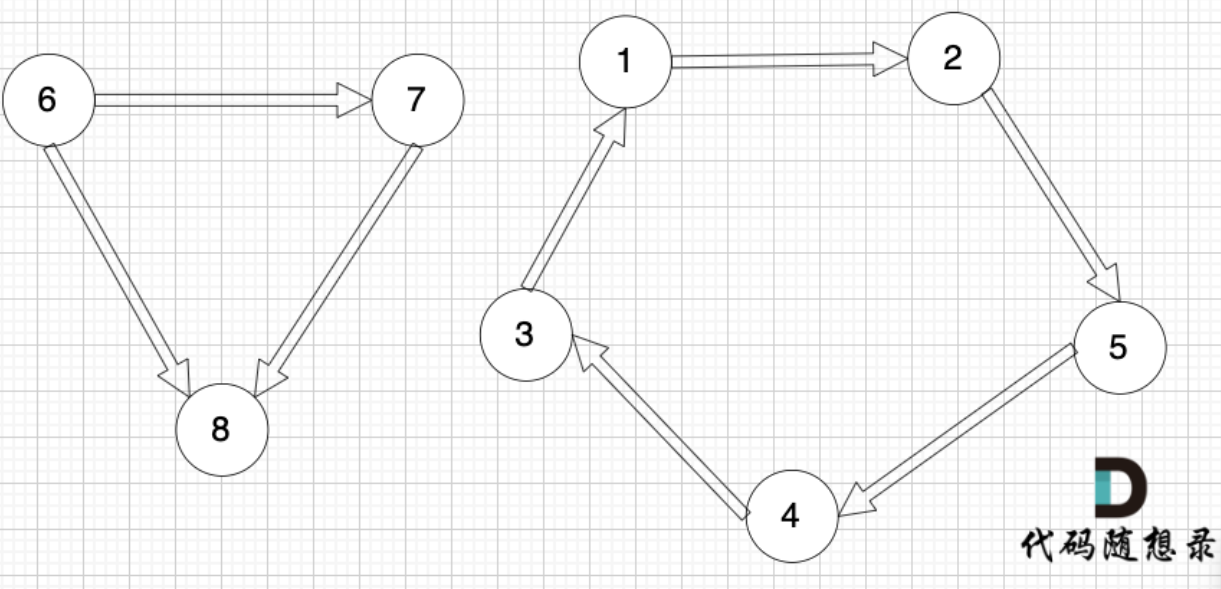
  • 强连通分量：有向图中，极大强连通子图称之为该图的强连通分量；如下图（6,7,8）和（1,2,3,4,5）的图；
    

• 图的构造

  • 邻接表；邻接矩阵；类；
  • 朴素存储；邻接表；邻居矩阵；

• 邻接矩阵

  • 二维数组表示图结构；
  • 节点表示图
  • grid[2][5]=6 grid[5][2]=6 说明grid中2和5节点中有一边；

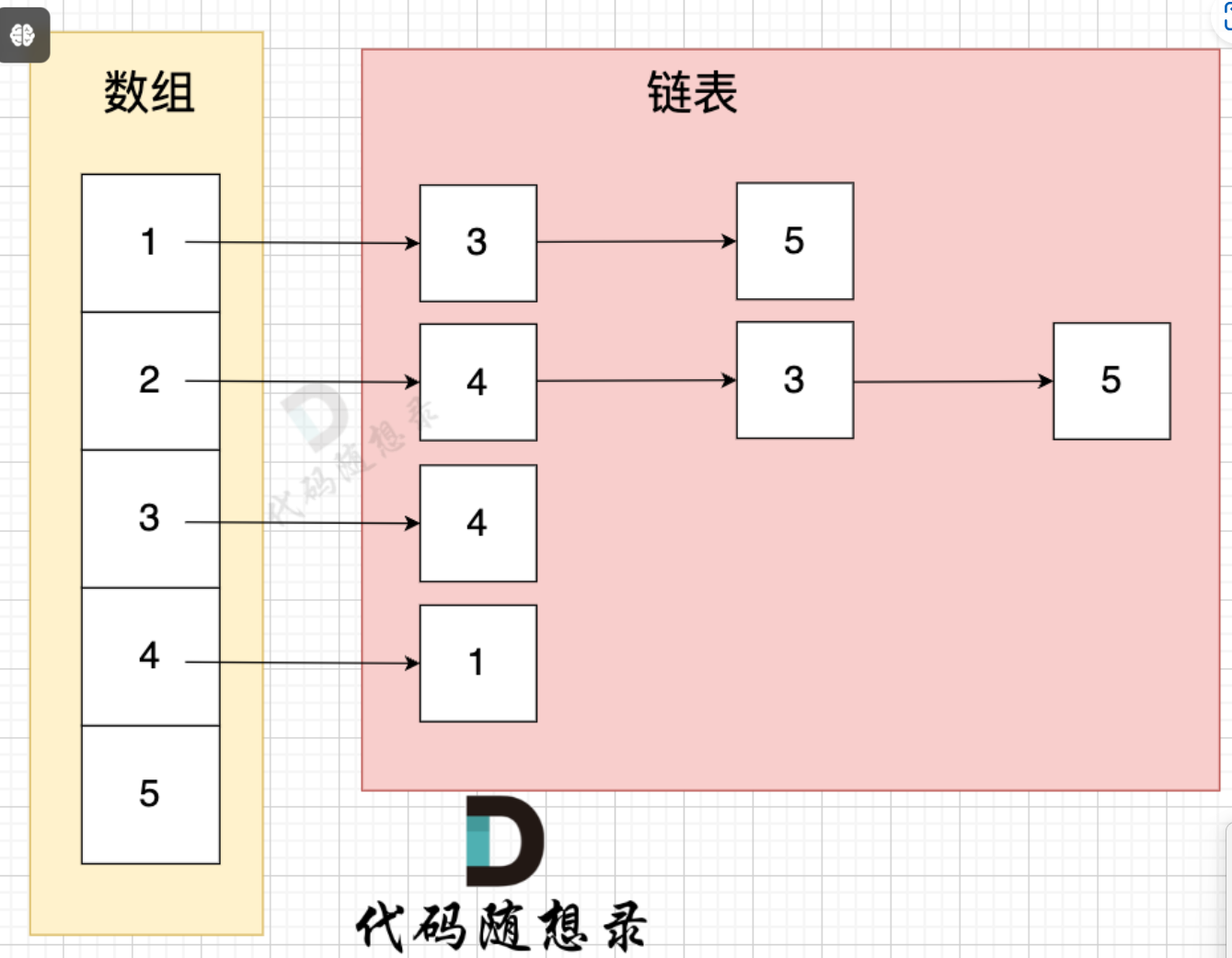
• 邻接表

  • 数组+链表；
  • 从边的角度存储图
    

图的遍历方式

• 深度优先搜索（dfs）
• 广度优先搜索（bfs）

深度优先搜索理论基础

概念

• 向一个方向搜索，遇到绝境就回溯，继续；

代码框架

• 因为有路径回溯和路径选择；
• 所以是递归+回溯的过程；

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

深搜三部曲

1. 确认递归函数、参数；

void dfs(参数)

• 二维数组保存所有路径；路径以一维数组保持；
• 全局变量保存

2. 确认终止条件；

if (终止条件) {
    存放结果;
    return;
}

3. 处理目前搜索节点出发的路径；

for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

98. 所有可达路径

题解

采用邻接矩阵方式

• 该方式采用邻接矩阵方式存储数据
• 严格按照模版进行遍历

点击查看代码

```python
def dfs(graph,x,n,res,path):
	if x==n:
		res.append(path.copy())
		return
	for i in range(1,n+1):
		if graph[x][i]==1:
			path.append(i)
			dfs(graph,i,n,res,path)
			path.pop()

def main():
	n,m = map(int,input().split())
	graph =[[0]*(n+1) for _ in range(n+1)]
	for i in range(m):
		s,t = map(int,input().split())
		graph[s][t] = 1
	path = [1]
	res = []
	dfs(graph,1,n,res,path)
	if not res:
		print(-1)
		return
	for path in res:
		print(" ".join(map(str,path)))
if __name__ == '__main__':
	main()
```
</details>

采用邻接列表方式

• 采用 from collections import defaultdict方式

  点击查看代码

  from collections import defaultdict
  def dfs(graph,x,n,path,res):
  	if x==n:
  		res.append(path.copy())
  		return
  	for i in graph[x]:
  		path.append(i)
  		dfs(graph,i,n,path,res)
  		path.pop()
  def main():
  	n,m = map(int,input().split())
  	graph = defaultdict(list)
  	for i in range(m):
  		s,t = map(int,input().split())
  		graph[s].append(t)
  	# print(graph)
  	res = []
  	path = [1]
  	dfs(graph,1,n,[1],res)
  	if not res:
  		print(-1)
  	else:
  		for path in res:
  			print(" ".join(map(str,path)))
  
  if __name__ == '__main__':
  	main()
  

广度优先搜索理论基础

使用场景

• 解决两点之间的最短路径问题
• 不涉及具体遍历方式，只要把相邻和相同属性的节点标记上即可；

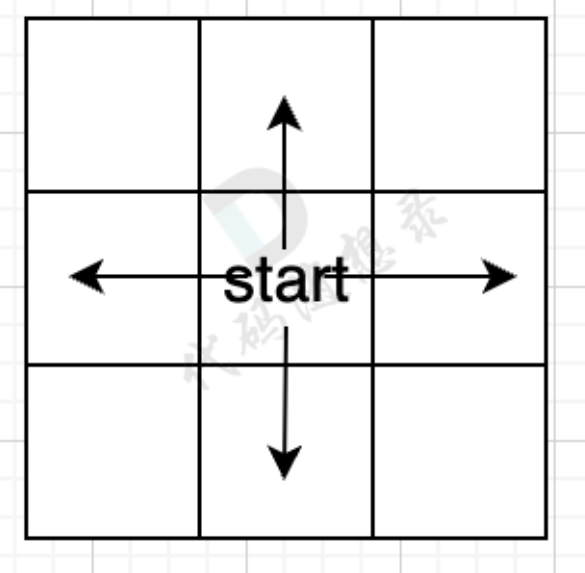
广搜过程

• 一圈一圈搜索