BZOJ 3774 最优选择 (最小割)

题面

中文题面,不解释liao:传送门

分析

好难啊,好神啊,这题我理解了好久(可能还没有真正理解?)

我们先假设所有点都满足条件得到了回报,回报之和为$sum$,那么最终的答案一定是$sum$减去一部分代价再减去一部分没有满足的点的回报.我们的任务就是求减去的一坨的最小值.所以我们将这个问题转化为求最小割的问题.

现在看看怎么转化.首先因为是四联通,所以可以像国际象棋棋盘一样黑白点染色,看作二分图来连边.一个点如果要得到回报,要么是自己被控制,要么是自己不被控制且四周都被控制.那么分这两种情况拆点,拆成$u_0$和$u_1$.

假设$u$是白点,$v$是某个与$u$相邻的黑点,括号内表示边权,连边的方式就是$\begin{aligned} &1.S\to u_0 (a_u) \\ &2.v_0\to T (a_v) \\ &3.u_0\to u_1 (b_u) \\ &4.v_1\to v_0 (b_v) \\ &5.u1\to v0 (\infty) \\ &6.u0\to v1 (\infty) \\ \end{aligned}$
画出来就是这个样子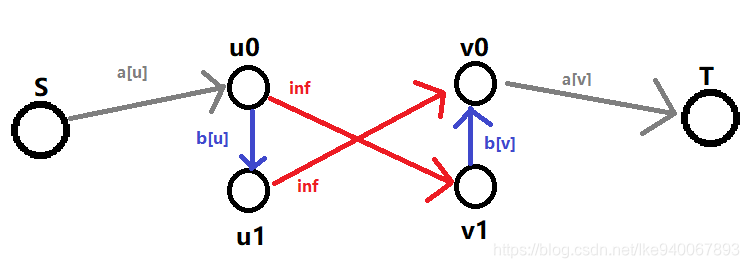
因为是求最小割,那么最后必须割成 从$S\to T$没有增广路.下面看看这样建图有什么妙处

• 因为中间两条红色的边权为$\infty$,所以不可能被割掉.
• 如果任意割掉两条灰色的边其一,那么这里就不会有增广路径,相当于控制了割掉的边对应的点并付出了相应代价.而此时如果没被割掉的点所相邻的四个点都已经割掉了灰色的边,那么这个点就被控制了,而且不用付出代价
• 如果两个点都不被控制,那么这两个点一定都不能得到回报,也就是割掉两条蓝色的边的情况,相当于舍弃了这两个点的回报.
  如此一来我们巧妙地满足了题目的要求(反正我第一次做想不到).
  那么这样求一次最小割就能得到(要舍弃的回报 $+$ 付出的代价) 的最小值,然后就求出了答案

边一般我都开得很大…懒得算
据说二分图的$dinic$跑得很快.同机房高一清华一本爷(见友链)说$O(n\sqrt n)$(甩锅 )

CODE

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
template<typename T>inline void read(T &num) {
    char ch; while((ch=getchar())<'0'||ch>'9');
    for(num=0;ch>='0'&&ch<='9';num=num*10+ch-'0',ch=getchar());
}

const int MAXN = 5010;
const int MAXM = 100005;
const int inf = 1e9;
const int dx[] = { 0, 0, 1, -1 };
const int dy[] = { 1, -1, 0, 0 };
int n, m, S, T, a[55][55], b[55][55];
int fir[MAXN], info[MAXN], cnt;
struct edge { int to, nxt, c; }e[MAXM];
inline void add(int u, int v, int cc) {
	e[cnt] = (edge){ v, fir[u], cc }; fir[u] = cnt++;
	e[cnt] = (edge){ u, fir[v], 0 }; fir[v] = cnt++;
}
int q[MAXN], vis[MAXN], cur, dis[MAXN];
inline bool bfs() {
	int head = 0, tail = 0;
	vis[S] = ++cur; q[tail++] = S;
	while(head < tail) {
		int u = q[head++];
		for(int i = fir[u]; ~i; i = e[i].nxt)
			if(e[i].c && vis[e[i].to] != cur)
				dis[e[i].to] = dis[u] + 1, vis[e[i].to] = cur, q[tail++] = e[i].to;
	}
	if(vis[T] == cur) memcpy(info, fir, sizeof fir);
	return vis[T] == cur;
}
int dfs(int u, int Max) {
	if(u == T || Max == 0) return Max;
	int flow = 0, delta;
	for(int &i = info[u]; ~i; i = e[i].nxt)
		if(e[i].c && dis[e[i].to] == dis[u] + 1 && (delta=dfs(e[i].to, min(Max-flow, e[i].c)))) {
			e[i].c -= delta, e[i^1].c += delta, flow += delta;
			if(flow == Max) return flow;
		}
	return flow;
}
inline int dinic() {
	int flow = 0, x;
	while(bfs()) {
		while((x=dfs(S, inf)))
			flow += x;
	}
	return flow;
}
inline int enc(int i, int j, bool k) { return (i-1)*m + j + k*n*m; }
inline void build() {
	S = 2*n*m + 1, T = 2*n*m + 2;
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= m; ++j) {
			if((i+j) & 1) {
				add(S, enc(i, j, 0), a[i][j]);
				add(enc(i, j, 0), enc(i, j, 1), b[i][j]);
			}
			else {
				add(enc(i, j, 0), T, a[i][j]);
				add(enc(i, j, 1), enc(i, j, 0), b[i][j]);
			}
			for(int l = 0, x, y; l < 4; ++l)
				if((x=i+dx[l]) >= 1 && x <= n && (y=j+dy[l]) >= 1 && y <= m)
					if((i+j) & 1) add(enc(i, j, 0), enc(x, y, 1), inf), add(enc(i, j, 1), enc(x, y, 0), inf);
		}
}
int main ()
{
	memset(fir, -1, sizeof fir);
    read(n), read(m);
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= m; ++j)
			read(a[i][j]);
	int sum = 0;
	for(int i = 1; i <= n; ++i)
		for(int j = 1; j <= m; ++j)
			read(b[i][j]), sum += b[i][j];
	build();
	printf("%d\n", sum-dinic());
}