Acwing 数论打卡(2)

873. 欧拉函数

https://www.acwing.com/video/298/
欧拉函数定义有f(x)=n 表示1到x中与x互质的数有n个

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
int fun(int x){
    int res=x;
    for(int i=2;i<=x/i;i++){
        if(x%i==0){
            res=res/i*(i-1);//先除后乘 避免数据溢出
            while(x%i==0) x/=i;
        }
    }
    if(x>1) res=res/x*(x-1);
    return res;
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int a;
        scanf("%d",&a);
        cout<<fun(a)<<endl;
    }
  return 0;
}
//  freopen("testdata.in", "r", stdin);

874. 筛法求欧拉函数

https://www.acwing.com/problem/content/876/

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1000010;


int primes[N], cnt;
int euler[N];
bool st[N];


void get_eulers(int n)
{
    euler[1] = 1;
    for (int i = 2; i <= n; i ++ )
    {
        if (!st[i])
        {
            primes[cnt ++ ] = i;
            //如果p是素数 那么欧拉函数值为p-1
            euler[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; j ++ )
        {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0)
            {
                euler[t] = euler[i] * primes[j];
                //因为pj是i的一个质因数 所以pj*i的质因数和i的质因数完全一样
                //欧拉函数f(n)=n*(1-1/p1)---(1-1/pn);
                //f(i)=i*(1-1/p1)---(1-1/pn);
                //f(pj*i)=pj*i*(1-1/p1)---(1-1/pn);
                //由于p1-pn完全相同 所以有f(pj*i)=pj*f(i);
                break;
            }
            //i%pj!=0
            //i*pj比i多了一个pj质因数 
            euler[t] = euler[i] * (primes[j] - 1);
        }
    }
}


int main()
{
    int n;
    cin >> n;

    get_eulers(n);

    LL res = 0;
    for (int i = 1; i <= n; i ++ ) res += euler[i];

    cout << res << endl;

    return 0;
}

875. 快速幂

https://www.acwing.com/problem/content/877/

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
int n;
int a,b,p;
//a的b次方%p
long long fun(int a,int b,int p){
    long long ans=1;
    long long temp=a;
    while(b){
        if(b&1) ans=ans*temp%p;
        temp=temp*temp%(long long )p;
        b>>=1;
    }
    return ans;
}
int main(){
    cin>>n;
    while(n--){
        scanf("%d%d%d",&a,&b,&p);
        printf("%lld\n",fun(a,b,p));
    }
  return 0;
}
//  freopen("testdata.in", "r", stdin);

876. 快速幂求逆元

https://www.acwing.com/problem/content/878/

乘法逆元简单来说就是对于一个数b，找到一个数x。有b*x同余与1%p 则x为b在1%p条件下的逆元。
题目条件b与p互质。 由费马定理有b的p-1次方 同余与1%p.
所以在这种条件下b的逆元就是b的p-2次方。

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
int n;
int a,b,p;
//a的b次方%p
long long fun(int a,int b,int p){
    long long ans=1;
    long long temp=a;
    while(b){
        if(b&1) ans=ans*temp%p;
        temp=temp*temp%(long long )p;
        b>>=1;
    }
    return ans;
}
int main(){
    cin>>n;
    while(n--){
        scanf("%d%d",&b,&p);
        long long res=fun(b,p-2,p);
        if(b%p) cout<<res<<endl;
        else puts("impossible");
    }
  return 0;
}
//  freopen("testdata.in", "r", stdin);

AcWing 877. 扩展欧几里得算法

https://www.acwing.com/activity/content/problem/content/946/1/

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
int exgcd(int a,int b,int &x,int &y){
    if(b==0){
        //gcd(a,b) b==0 return a
        //有ax+by=a; x=1 y规定为0
        x=1;
        y=0;
        return a;
    }
    else {
        int d=exgcd(b,a%b,y,x);
        y-=a/b*x;
        return d;
    }
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int a,b;
        cin>>a>>b;
        int x,y;
        exgcd(a,b,x,y);
        printf("%d %d\n",x,y);
    }
  return 0;
}
//  freopen("testdata.in", "r", stdin);

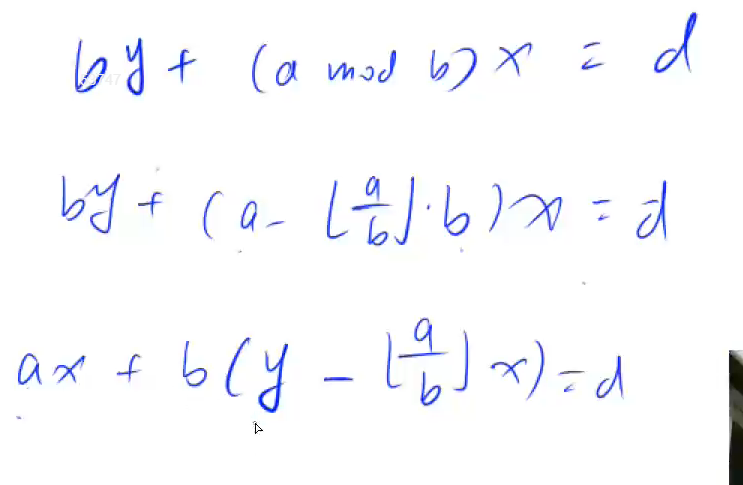
根据上图推出y-=a/b*x

878. 线性同余方程

https://www.acwing.com/problem/content/880/

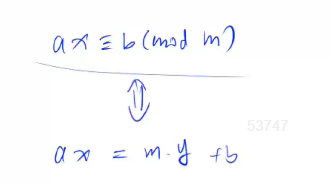
ax除m 余数是b 可以转化为ax=y倍的m+b

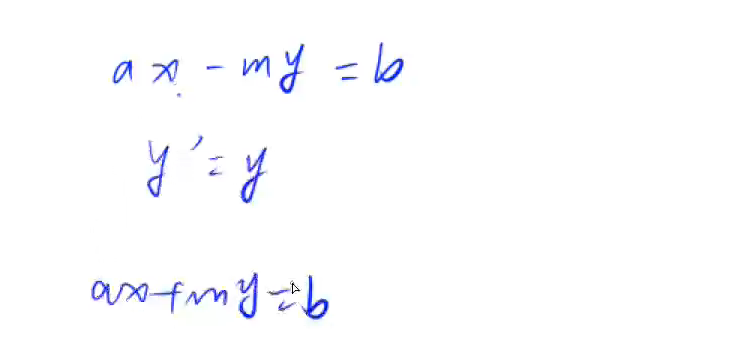
吧符号取到y里面,就变成扩展欧几里得了 当然前提是b是gcd(a,m)的倍数

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
int exgcd(int a,int b,int &x,int &y){
    if(b==0){
        //gcd(a,b) b==0 return a
        //有ax+by=a; x=1 y规定为0
        x=1;
        y=0;
        return a;
    }
    else {
        int d=exgcd(b,a%b,y,x);
        y-=a/b*x;
        return d;
    }
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int a,b,m;
        cin>>a>>b>>m;
        int x,y;
        int d=exgcd(a,m,x,y);
        if(b%d!=0) puts("impossible");
        else printf("%d\n",(long long )(b/d)*x%m);
    }
  return 0;
}
//  freopen("testdata.in", "r", stdin);